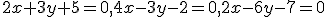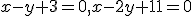Vektorový a afinný priestor
Cvičenie
Vektory a počítanie s nimi
- Vyriešte sústavu rovníc s parametrom
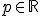 v obore
v obore 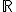 a tiež v obore
a tiež v obore 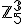
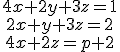 .
.
Pozrite si geometrickú interpretáciu Tu. - Vyriešte sústavu rovníc v obore
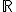
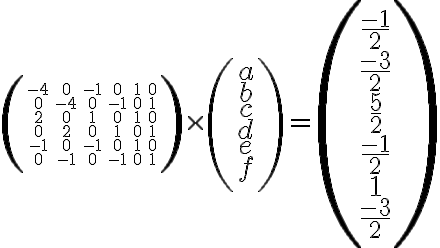 .
.
Pozrite si geometrickú interpretáciu Tu. - Zistite, či množina
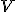 všetkých usporiadaných dvojíc resp. trojíc spolu s dvoma binárnymi operáciami
všetkých usporiadaných dvojíc resp. trojíc spolu s dvoma binárnymi operáciami 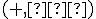 je vektorovým priestorom nad poľom reálnych
čísel
je vektorovým priestorom nad poľom reálnych
čísel 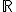 , ak
, ak
- Sú dané body
![\small A=[-1,2], \;B=[5,1] ,\;C=[1,3] \small A=[-1,2], \;B=[5,1] ,\;C=[1,3]](https://lms.umb.sk/filter/tex/pix.php/414c0526ae587c59bf7ca2b03f363dfc.png) . Nájdite vektory
. Nájdite vektory
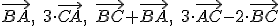
a zistite ich dĺžky. Zadanie Tu. - [Mon 1.1.3.] Sú dané body
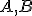 . Určte polohu bodu
. Určte polohu bodu 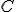 tak, aby
tak, aby
- V rovine je daný pravidelný 6-uholník
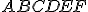 .
.
- K vektorom
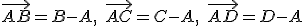 nájdite ďalšie orientované úsečky, ktoré reprezentujú dané vektory.
nájdite ďalšie orientované úsečky, ktoré reprezentujú dané vektory.
Otvorte si model šesťuholníka Tu. - Určte koľko viazaných (voľných) vektorov je určených vrcholmi pravidelný 6-uholník
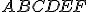 .
.
- K vektorom
- [Monoszová 1.1.11.] až [Monoszová 1.1.17.] Zbierka úloh z analytickej geometrie. Prvá časť Tu.
- Daný je pravidelný šesťuholník
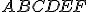 . Vyjadrite vektory
. Vyjadrite vektory
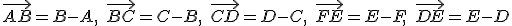
ako lineárne kombinácie vektorov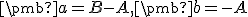 .
. - V rovine je daný šesťuholník, ktorého vrcholy sú určené vzťahmi:
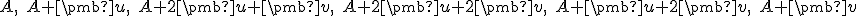 .
.
Dokážte, že tento šesťuholník je súmerný podľa stredu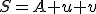 .
Zadanie Tu.
Riešenie Tu.
.
Zadanie Tu.
Riešenie Tu. - Nech
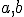 sú nekolineárne vektory. Určte číslo
sú nekolineárne vektory. Určte číslo 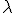 tak, aby vektory
tak, aby vektory
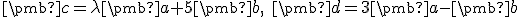 boli kolineárne.
boli kolineárne. - Ukážte, že vektor
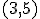 je lineárnou kombináciou vektorov
je lineárnou kombináciou vektorov 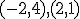 ale nie je LK vektorov
ale nie je LK vektorov 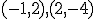 .
. - Vyjadrite vektor
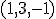 ako LK vektorov
ako LK vektorov 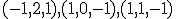 .
. - Ukážte, že vektory
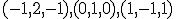 sú lineárne (ne)závislé.
sú lineárne (ne)závislé. - Vyjadríte vektor
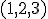 ako lineárnu kombináciu vektorov
ako lineárnu kombináciu vektorov 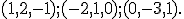
- Nech vektory
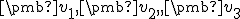 sú lineárne nezávislé. Zistite, či vektory
sú lineárne nezávislé. Zistite, či vektory
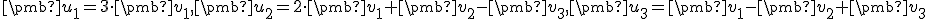 sú závislé alebo nezávislé.
sú závislé alebo nezávislé.
- Množina
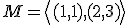 je báza vektorového priestoru
je báza vektorového priestoru 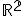 . Určte
súradnice vektora
. Určte
súradnice vektora 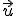 vzhľadom k tejto báze, ak poznáte jeho súradnice
vzhľadom k tejto báze, ak poznáte jeho súradnice 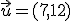 vzhľadom
ku kanonickej báze
vzhľadom
ku kanonickej báze 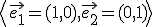 . [Hašek 4.2.]
. [Hašek 4.2.] - Daný je vektorový priestor
![\small W=[(1,0,2),(2,4,1),(1,2,3)]⊂\mathbb{\pmb Z^3_5} \small W=[(1,0,2),(2,4,1),(1,2,3)]⊂\mathbb{\pmb Z^3_5}](https://lms.umb.sk/filter/tex/pix.php/bf39545fa9089af780723cfab823fb3c.png) .
.
- Nech
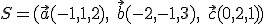 je báza priestoru
je báza priestoru 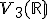 .
Nájdite vektor vo
.
Nájdite vektor vo 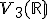 , ktorého súradnice vzhľadom k báze
, ktorého súradnice vzhľadom k báze  sú
sú 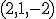 .
. - [Hašek 4.6.1] až [Hašek 4.6.8] Linearni algebra a geometrie. Dostupné Tu.
- Vypočítajte veľkosti uhlov a dĺžky strán v trojuholníku
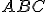 , ak .
, ak .![\small A = [1,-2],\; B = [-3,3],\; C = [1,3] \small A = [1,-2],\; B = [-3,3],\; C = [1,3]](https://lms.umb.sk/filter/tex/pix.php/3bef5eb33c3054007f7c722fa39fe506.png) . Riešenie
...
. Riešenie
... - Vypočítate uhol vektorov
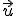 a
a 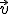 , ak
, ak 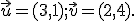
- Nech
![\small A = [1, 3], B = [-1, 5], \vec u=(2,-5), \vec v= (−3, 1) \small A = [1, 3], B = [-1, 5], \vec u=(2,-5), \vec v= (−3, 1)](https://lms.umb.sk/filter/tex/pix.php/017902b88f3a72c0913426327244e220.png) . Rozhodnite,
či napísaný objekt je bod alebo vektor a určte jeho súradnice.
. Rozhodnite,
či napísaný objekt je bod alebo vektor a určte jeho súradnice.
a)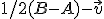
b)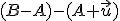 [
[
c)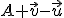
- [Monoszová 2.1.1.] až [Monoszová 2.1.23.] Zbierka úloh z analytickej geometrie. Druhá časť Tu.
- [Monoszová 2.2.1.] až [Monoszová 2.3.7.] Zbierka úloh z analytickej geometrie. Druhá časť Tu.
- [Monoszová 1.2.1.a] Riešenie alg. Tu; geom. Tu.
- [Monoszová 1.2.1.b] Riešenie Tu.
- [Monoszová 1.2.2.a] Riešenie Tu.
- [Monoszová 1.2.4 ] Riešenie Tu.
- [Monoszová 1.2.5.b] Riešenie Tu.
- [Monoszová 1.2.5.c] Riešenie alg. Tu; geom. Tu.
- Riešte úlohy [Monoszová 1.3.1.] až [Monoszová 1.3.5.].
- Vypočítajte súradnice bodu
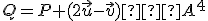 v afinnej súradnicovej sústave
v afinnej súradnicovej sústave
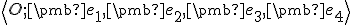 ,
ak
,
ak 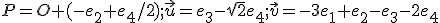 .
. - V rovine danej bodmi
![\small A = [2, 1, 3], B = [2, 4, 0], C = [−3, 0, 4] \small A = [2, 1, 3], B = [2, 4, 0], C = [−3, 0, 4]](https://lms.umb.sk/filter/tex/pix.php/9677c54bd1d6db96f81dc0bb8cea97d5.png) zvoľte afinnú súradnicovú sústavu
zvoľte afinnú súradnicovú sústavu
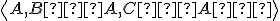 . Zistite, aké súradnice má bod M v
. Zistite, aké súradnice má bod M v 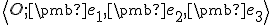 , ak jeho
súradnice v
, ak jeho
súradnice v 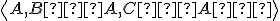 sú
sú ![\small [5, 3]) \small [5, 3])](https://lms.umb.sk/filter/tex/pix.php/0e8d92d16f33e2ae254b91b3e18618ac.png) .
. - V rovine je daný trojuholník
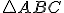 a body
a body 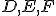 v tomto poradí ako stredy strán
v tomto poradí ako stredy strán 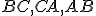 . Nájdite súradnice vrcholov trojuholníka
v afinnej sústave súradníc
. Nájdite súradnice vrcholov trojuholníka
v afinnej sústave súradníc 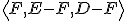 .
. - V rovine je daný pravidelný šesťuholník
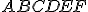 . Nájdite súradnice vrcholov tohto 6-uholníka v afinnej súradnicovej
sústave
. Nájdite súradnice vrcholov tohto 6-uholníka v afinnej súradnicovej
sústave 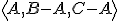 .
.
- Riešte úlohy [Monoszová 1.4.1.] až [Monoszová 1.4.18.].
- Zistite, či body
![\small M = [9,-2,5], N = [4, 1, 6] \small M = [9,-2,5], N = [4, 1, 6]](https://lms.umb.sk/filter/tex/pix.php/974bd421bfa210dda41cb67d18699651.png) incidujú s podpriestorom
incidujú s podpriestorom 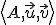 pre
pre ![\small A = [1, 3, 2], \vec u = (2, -1, 1), \vec v = (1, -1, 0) \small A = [1, 3, 2], \vec u = (2, -1, 1), \vec v = (1, -1, 0)](https://lms.umb.sk/filter/tex/pix.php/7859ecad3fa4ae689582f603a2d07df6.png) .
.
Návod: Bod leží v podpriestore práve vtedy, keď jeho súradnice vyhovujú parametrickému vyjadreniu, t. j.:
leží v podpriestore práve vtedy, keď jeho súradnice vyhovujú parametrickému vyjadreniu, t. j.:
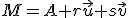 . Napíšte najskôr parametrické rovnice podpriestoru a dosaďte súradnice bodu
. Napíšte najskôr parametrické rovnice podpriestoru a dosaďte súradnice bodu  . [Vranková, 3L1].
. [Vranková, 3L1]. - Dokážte, že pre každé
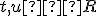 množina bodov
množina bodov ![\small {[1, 0, 1], [3, 3, 5], [4, 1, 6], [1 + 2t + 3u, 3t + u, 1 + 4t + 5u]} \small {[1, 0, 1], [3, 3, 5], [4, 1, 6], [1 + 2t + 3u, 3t + u, 1 + 4t + 5u]}](https://lms.umb.sk/filter/tex/pix.php/47428d8eb79f10991d01b3c4d0d55664.png) priestoru
priestoru 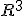 je afinne závislá.
Akú dimenziu má jej afinný obal?
je afinne závislá.
Akú dimenziu má jej afinný obal? - Určte aspoň jedno parametrické vyjadrenie roviny, ktorá prechádza bodom
![\small N = [-2, 3, 0] \small N = [-2, 3, 0]](https://lms.umb.sk/filter/tex/pix.php/025567a1d3ab183d7657bf4c2715170b.png) a obsahuje priamku
a obsahuje priamku
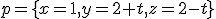 .
. - Riešte úlohy z práce (Tisoň, 2011) k téme: Lineárne podpriestory, parametrické a všeobecné vyjadrenia.
- Vyšetrite vzájomnú polohu danej priamky
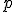 a roviny
a roviny 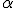 v
v 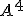 , ak:
, ak: 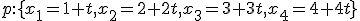 ,
, 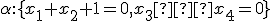 . [Vranková, 4L1].
. [Vranková, 4L1]. - Zistite vzájomnú polohu priamky
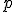 a roviny
a roviny 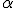 v
v 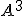 , ak
, ak 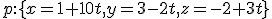 ,
, 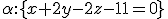 .
. - Zistite vzájomnú polohu priamok
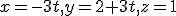
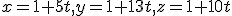
- Určte afinné zobrazenie
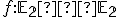 zobrazujúce
repér
zobrazujúce
repér 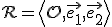 :
Vo všetkých prípadoch určte množinu samodružných bodov.
:
Vo všetkých prípadoch určte množinu samodružných bodov.
- Afinné zobrazenie
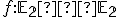 je dané transformačnými rovnicami
je dané transformačnými rovnicami 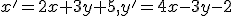 . Určte
. Určte
- Dané je afinné zobrazenie
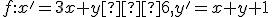 . Určite
. Určite
- Určte afinné zobrazenie, pre ktoré sú body priamky
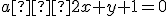 samodružné a bod [0, 0] sa zobrazí do [−1, −2].
samodružné a bod [0, 0] sa zobrazí do [−1, −2]. - Dané je afinné zobrazenie
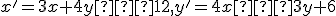 . Na priamke
. Na priamke 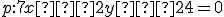 nájdite bod
nájdite bod 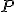 ,
ktorého obraz leží na tej istej priamke. Pomoc: najskôr určte obraz
,
ktorého obraz leží na tej istej priamke. Pomoc: najskôr určte obraz 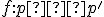 a potom priesečník (\small P= p\cap p' \). Priamku
a potom priesečník (\small P= p\cap p' \). Priamku 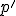 určte aj konštrukčne ako GMB.
určte aj konštrukčne ako GMB.
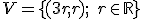
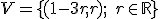
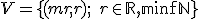
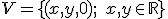
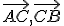
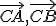
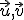
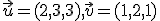
![\small [(1,0,2),(2,4,1),(1,2,3)] \small [(1,0,2),(2,4,1),(1,2,3)]](https://lms.umb.sk/filter/tex/pix.php/4d1541748ff79167ba18023859b5bd6a.png)
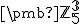
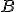
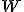
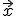
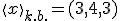
![\small O=[0, 0],\overrightarrow{e_1}= [1, 0], \overrightarrow{e_2}=[0, 1] \small O=[0, 0],\overrightarrow{e_1}= [1, 0], \overrightarrow{e_2}=[0, 1]](https://lms.umb.sk/filter/tex/pix.php/3bc082c1ca429d3d532b6d2ac1885e88.png)
![\small O'=[1, 1], \overrightarrow{e'_1}=[0, 1], \overrightarrow{e'_2}=[ 1 , 0] \small O'=[1, 1], \overrightarrow{e'_1}=[0, 1], \overrightarrow{e'_2}=[ 1 , 0]](https://lms.umb.sk/filter/tex/pix.php/a901128b615bb55454fdd7633d9cce87.png)
![\small O'=[0, 0], \overrightarrow{e'_1}=[-1, 0], \overrightarrow{e'_2}=[ 0 , -1 \small O'=[0, 0], \overrightarrow{e'_1}=[-1, 0], \overrightarrow{e'_2}=[ 0 , -1](https://lms.umb.sk/filter/tex/pix.php/5a58875d8d23211cfcb29a9f67520846.png)