Vedecké poznávanie vo vyučovaní matematiky
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Vedecké poznávanie vo vyučovaní matematiky |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 13:21 |
Názornosť v matematike
Nech je daná množina 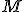 a
a 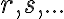 sú relácie na nej definované. Štruktúru
sú relácie na nej definované. Štruktúru 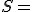
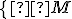 môžeme považovať za popis alebo model určitej udalosti. Označme
môžeme považovať za popis alebo model určitej udalosti. Označme 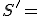
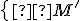 obraz štruktúry
obraz štruktúry 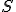 v morfizme
v morfizme 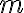 .
.
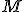 a
a 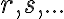 sú relácie na nej definované. Štruktúru
sú relácie na nej definované. Štruktúru 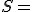
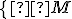 môžeme považovať za popis alebo model určitej udalosti. Označme
môžeme považovať za popis alebo model určitej udalosti. Označme 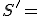
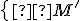 obraz štruktúry
obraz štruktúry 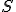 v morfizme
v morfizme 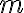 .
.
Model 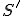 budeme považovať za názornejší než model
budeme považovať za názornejší než model 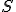 vtedy a len vtedy, ak subjekt získava z neho informácie efektívnejšie než z modelu
vtedy a len vtedy, ak subjekt získava z neho informácie efektívnejšie než z modelu 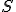 .
Názornejší model1) je teda pre určitý subjekt zrozumiteľnejší, než model pôvodný.
.
Názornejší model1) je teda pre určitý subjekt zrozumiteľnejší, než model pôvodný.
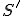 budeme považovať za názornejší než model
budeme považovať za názornejší než model 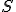 vtedy a len vtedy, ak subjekt získava z neho informácie efektívnejšie než z modelu
vtedy a len vtedy, ak subjekt získava z neho informácie efektívnejšie než z modelu 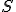 .
Názornejší model1) je teda pre určitý subjekt zrozumiteľnejší, než model pôvodný.
.
Názornejší model1) je teda pre určitý subjekt zrozumiteľnejší, než model pôvodný.
Formy, prostriedky, metódy a spôsoby znázorňovania.
Súčasná didaktika matematiky vyvinula rôzne efektívne spôsoby názornej a grafickej reprezentácie matematických myšlienok. V prvom rade sú to rôznorodé matematické symboliky, ktoré významne urýchlili pokrok matematickej vedy. Radia sa k nim:
Súčasná didaktika matematiky vyvinula rôzne efektívne spôsoby názornej a grafickej reprezentácie matematických myšlienok. V prvom rade sú to rôznorodé matematické symboliky, ktoré významne urýchlili pokrok matematickej vedy. Radia sa k nim:
- množinovo teoretický formalizmus
- Descartov súradný systém, grafy relácií a funkcií
- softvérové produkty (Maple, GeoGebra, a pod.)
- empiricko – konštruktívne spôsoby
- mentálne a pojmové mapy; iné grafické schémy
V súčasnosti sa dostávajú do popredia problémy v matematickom vzdelávaní, ktoré pramenia predovšetkým z:
- dlhodobo klesajúcej úrovne matematických vedomostí (zreteľne to vidieť pri prechode na vyšší stupeň vzdelávania)
- nedostatočného matematického zdôvodňovanie a argumentácie (mnohí učitelia len formálne sprostredkujú žiakom matematické tvrdenia)
- nevýrazné využívanie moderných technológií (ich (ne)používanie sa prejavilo hlavne pri online vyučovaní).
_____________________________________________________________
1) Formy, metódy, spôsoby a prostriedky, ako určitý model pretransformovať na model názornejší sú rôznorodé. (Kuřina, 2000)
1) Formy, metódy, spôsoby a prostriedky, ako určitý model pretransformovať na model názornejší sú rôznorodé. (Kuřina, 2000)
Problémové vyučovanie
Pri problémovom vyučovaní žiak je postavený pred problém, ktorý musí riešiť sám. Východiskom pri problémovom vyučovaní ja formulovanie problému, ktorý žiak by mal riešiť a pritom objavovať nové poznatky a vzťahy medzi nimi.
Problémové vyučovanie predstavuje taký typ vyučovania, pri ktorom žiaci samostatne riešia teoretické alebo praktické problémy, teda žiak je viac činný ako učiteľ.1)
- Pod matematickým problémom budeme rozumieť situáciu, v ktorej riešiteľ (vybraná osoba) má nájsť cestu z danej východiskovej situácie k vytýčenému cieľu, pričom pri hľadaní takejto cesty sú nevyhnutné určité matematické pojmy a princípy.
- Podstatou problémového vyučovania je vytváranie problémových situácií (formulovanie problému) a usmerňovanie činnosti žiaka pri hľadaní cesty, ktorá sa na začiatku javí ako neprekonateľná.
- Hlavným prínosom problémového vyučovania je podnietenie (aktivácia) žiakovej tvorivosti, rozvoj samostatnosti a upevňovanie zodpovednosti za svoju prácu. Nevýhodou problémových úloh je veľká časová náročnosť a rozdielna vedomostná úroveň žiakov.
Problémové vyučovanie uskutočňujeme hlavne prostredníctvom týchto dvoch metód:
- výskumná metóda
- heuristická metóda
Úloha
Pokúste sa odvodiť vzorec pre výpočet - tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice
- tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice 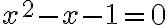 .
.
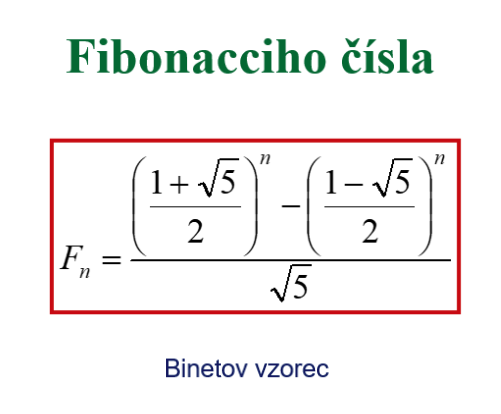 ...
...
Pokúste sa odvodiť vzorec pre výpočet
 - tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice
- tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice 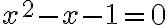 .
.
 ...
...
____________________________________________________________________________________________
1) Koníčková, J.: Chcete naučiť žiakov riešiť problémy? Vyskúšajte problémové vyučovanie. Dostupné na EduWord.sk Tu
1) Koníčková, J.: Chcete naučiť žiakov riešiť problémy? Vyskúšajte problémové vyučovanie. Dostupné na EduWord.sk Tu
Výskumná metóda
Výskumná metóda sa svojím charakterom približuje k výskumnej práci vedeckého pracovníka na vysokej škole. O výskumnej metóde v školskej matematike hovoríme vtedy, keď žiaci riešia problémy, ktoré veda už vyriešila a nové sú len zo subjektívneho hľadiska žiakov.
Učiteľ
- hlavný cieľ je naučiť žiakov ovládať metódy vedeckého poznávania
- pred formulovaním výskumného problému, žiakov najskôr vhodne motivuje
- formuluje výskumný problém, pričom ten musí zodpovedať intelektuálnym možnostiam žiakov. Zároveň musí byť dostatočne náročný ale jeho riešenie musí byť v možnostiach žiakov.
Žiaci
- na základe vlastného pozorovania a štúdia faktov vyslovujú čiastkové problémy
- skúmajú určité (konkrétne) situácie, formulujú hypotézy a zostavujú výskumný plán
- postupne hľadajú vlastný spôsob riešenia problému, dokazujú hypotézy
Poznámky.
- V školskej matematike je často nad rámec vedomostí žiakov dokázať sformulované hypotézy. V takom prípade overujeme platnosť hypotézy na konkrétnych príkladoch.
- Je potrebné mať na zreteli, že výskumný prístup je v školskej matematike len pracovnou metódou. Pomocou tejto metódy žiaci prenikajú do vnútornej krásy matematiky, a tak nadobúdajú lepší vzťah k nej samej.
Nepochybne medzi progresívne metódy pri riešení problémov v školskej matematike určite patrí aj výskumný prístup pri vyučovaní matematiky a zaraďovanie riešenia matematických problémov do vyučovania. Tento prístup je spracovaný v prácach profesora Kopku z UJEP v Ústí nad Labem. Do pozornosti študentom - budúcim učiteľom matematiky dávame tieto dve práce:
- Kopka, J.: Hrozny problému ve školské matematice. UJEP Ústí nad Labem 1999.
- Kopka, J.: Výskumný přístup při výuce matematiky. UJEP Ústí nad Labem 2004.
Profesor Kopka zdôrazňuje, že
- stratégia alebo taktika pri riešení problémov sa nazýva heuristika. Pozrite si ukážku Tu.
- výskumný prístup pri výučbe školskej matematiky sa v značnej miere opiera o experimentovanie.
- celý výskumný proces môžeme stotožniť so schémou: konkretizácia(špecializácia) → zovšeobecňovanie → vyslovenie hypotézy → dôkaz
Uvedená schéma je v súlade so štruktúrou separovaných a generických modelov, ktorú zaviedol profesor Hejný.
V ďalšej časti sa zameriame na niekoľko problémov, ktorých riešenie je podrobne popísané v spomínaných prácach prof. Kopku.
V ďalšej časti sa zameriame na niekoľko problémov, ktorých riešenie je podrobne popísané v spomínaných prácach prof. Kopku.
Cvičenie - problém
- Sú dané prvé tri členy postupnosti: 17, 27 a 47. Nájdite medzi nimi nejakú zákonitosť a vypíšte ďalšie členy postupnosti resp. určte vzorec pre výpočet
 - tého člena takej postupnosti.1)
- tého člena takej postupnosti.1) - Pokúste sa rozdeliť štvorec aj na iný počet štvorcov než štyri. Pritom sa nepožaduje, aby štvorce boli rovnako veľké.2)
________________________________________________________________
1) Kopka, J.: Výskumný přístup při výuce matematiky. UJEP Ústí nad Labem 2004. Str. 60.
2) Kopka, J.: Výskumný přístup při výuce matematiky. UJEP Ústí nad Labem 2004. Str. 93.
1) Kopka, J.: Výskumný přístup při výuce matematiky. UJEP Ústí nad Labem 2004. Str. 60.
2) Kopka, J.: Výskumný přístup při výuce matematiky. UJEP Ústí nad Labem 2004. Str. 93.
Palindromy
Čísla, ktoré sa čítajú rovnako odpredu aj odzadu, ako napríklad 452 254, sa nazývajú palindromy.
Úloha
Ukážte, že všetky štvorciferné palindromy sú deliteľné číslom 11.
Ukážte, že všetky štvorciferné palindromy sú deliteľné číslom 11.
Úloha je určená pre žiakov stredných škôl a je vhodná práve pre experimentovanie. Je dosť pravdepodobné, že žiaci nepoznajú pojem "palindrom". Z toho dôvodu by mal učiteľ ešte pred riadeným výskumným procesom, priblížiť žiakom na konkrétnych prípadoch pojem polindromu. Samotný priebeh heuristického skúmania s danej triede učiteľ koordinuje resp. usmerňuje pokynmi typu:
- Vypíšte náhodne niekoľko čísel, ktoré sú polyndromy: 4554 = 11 . 414, 1001 = 11 . 91, ...
- Koľko bude všetkých možností? (Je ich 90 - prečo? )
- Vypíšme niekoľko podľa veľkostí - 1001, 1111, 1221, 1331, 1441, ...
- Skúmajme vlastnosti tejto postupnosti - je aritmetická s diferenciou 110?
- Avšak pri "prechode" cez tisícky ... 1991, 2002, ... , 2992, 3003, ... - diferencia je 11!
- Prvé číslo 1010 = 11. 91 je deliteľné 11 a každé ďalšie tiež deliteľné 11
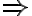 tvrdenie je pravdivé.
tvrdenie je pravdivé.
Mnohouholníkové čísla
Trojuholníkové čísla sú dané nasledujúcimi explicitnými vzorcami:

( T_{n}=\sum _{k=1}^{n}k=1+2+3+ \cdot \cdot \cdot +n={\frac {n(n+1)}{2}} \)

( T_{n}=\sum _{k=1}^{n}k=1+2+3+ \cdot \cdot \cdot +n={\frac {n(n+1)}{2}} \)
Súčet dvoch po sebe idúcich trojuholníkových čísel je
štvorcové číslo.
Figurálne (polygonálne) čísla s vyšším počtom strán môžu byť tiež graficky znázornené podľa tohto pravidla, hoci bodky už nebudú tvoriť dokonale pravidelnú mrežu, ako je uvedené vyššie.
- Pentagonálne čísla
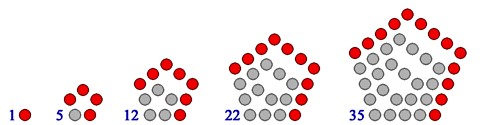
- Šesťuholníkové čísla
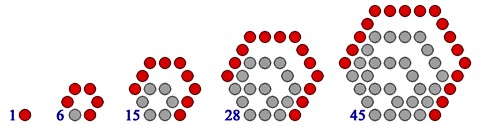
- Prezentácia k téme Tu
Zeleninový záhon
Problém
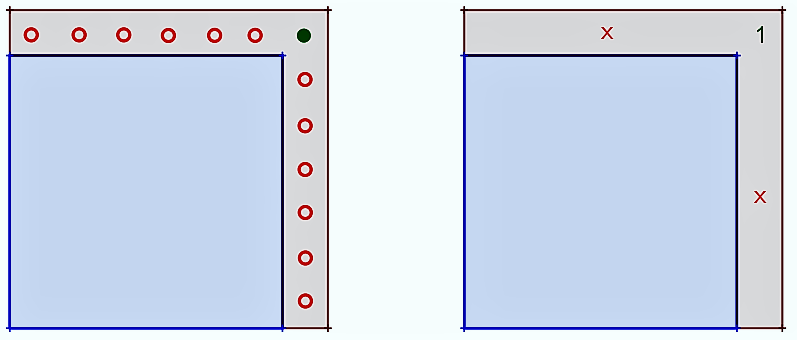
Farmár pestuje kapustu vždy v štvorcovom záhone. Tento rok obsahuje jeho štvorcový záhon o 23 hlávok kapusty viac ako vlani. Koľko hlávok kapusty pestuje tento rok?
Farmár pestuje kapustu vždy v štvorcovom záhone. Tento rok obsahuje jeho štvorcový záhon o 23 hlávok kapusty viac ako vlani. Koľko hlávok kapusty pestuje tento rok?
1. Experimentálne - počet hlávok je vyjadrený štvorcovým číslom
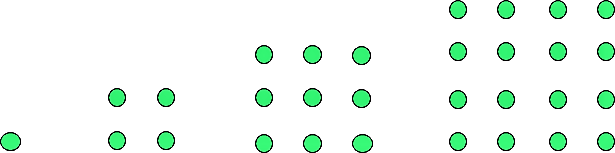 . . .
. . .
Riešením musia byť dve po sebe idúce štvorcové čísla, ktorých rozdiel je 23.
2. Tabuľkový procesor

Riešením sú štvorcové čísla: 121 - vlani, 144 - tento rok. Otvorte si Excel Tu.
Príklady sú prevzaté od profesora Kopku.
 . . .
. . .Riešením musia byť dve po sebe idúce štvorcové čísla, ktorých rozdiel je 23.
2. Tabuľkový procesor
Riešením sú štvorcové čísla: 121 - vlani, 144 - tento rok. Otvorte si Excel Tu.
Metóda dialógu
Učitelia matematiky by mali poznať definíciu pojmu na rôznych úrovniach vzdelávania a jeho rozsah. Napr. pri pojme druhá odmocnina nezáporného reálneho čísla je nutné si uvedomiť:
- Pojem odmocnina vo všeobecnom význame, ktorý poznajú z odbornej vysokoškolskej prípravy
- Rozsah v akom sa tento pojem zavádza v učive matematiky príslušného stupňa školy
- Spôsob akým pojem odmocnina budú prezentovať žiakom
Východiská pri zavádzaní pojmu odmocnina sú rôzne na nižšom stupni vzdelávania a vedeckým prístupom:
"Druhá mocnina a odmocnina" v 8. ročníku základnej školy ale aj na strednej škole
"Funkcia a funkcia inverzná" sú základnými pojmami už v prvom ročníku na vysokej škole.
Pri voľbe spôsobu zavádzania pojmu odmocnina majú učitelia k dispozícii "celú" pedagogiku, psychológiu a didaktiku matematiky.
"Druhá mocnina a odmocnina" v 8. ročníku základnej školy ale aj na strednej škole
"Funkcia a funkcia inverzná" sú základnými pojmami už v prvom ročníku na vysokej škole.
Pri voľbe spôsobu zavádzania pojmu odmocnina majú učitelia k dispozícii "celú" pedagogiku, psychológiu a didaktiku matematiky.
Druhá odmocnina I
Formulujme didaktický problém
Pri preberaní druhej odmocniny žiaci nedokážu uspokojivo odpovedať na otázku prečo nemôže byť
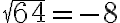 ,
,
keďže platí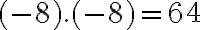 . Uvedieme dve ukážky od učiteľov z praxe.
. Uvedieme dve ukážky od učiteľov z praxe.
Pri preberaní druhej odmocniny žiaci nedokážu uspokojivo odpovedať na otázku prečo nemôže byť
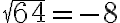 ,
,keďže platí
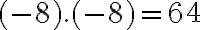 . Uvedieme dve ukážky od učiteľov z praxe.
. Uvedieme dve ukážky od učiteľov z praxe.
A. Metóda expozičná (metóda dialogická, metóda problémová, ZŠ - 8. ročník) Krajčiová, J.: Mocniny resp. Matematika v dialógoch
Učiteľov záver
A výsledky by boli dva? Aj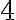 aj
aj 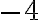 ? Preto sa matematici dohodli, že za výsledok sa vezme len číslo kladné, prípadne nezáporné. Už si môžeme definovať druhú odmocninu.
? Preto sa matematici dohodli, že za výsledok sa vezme len číslo kladné, prípadne nezáporné. Už si môžeme definovať druhú odmocninu.
Ž: No, vážne, ...prečo? Nezamýšľal som sa nad tým.
- U: Mnoho vecí (a nielen v matematike) používame dnes už automaticky. No cesta ich zavedenia bola kľukatá, plná dobrodružstiev. Nie je tomu ináč ani pri odmocnine.
-
Ž: Už som celý nedočkavý. Ako to teda s tou odmocninou je?
-
U: Znak odmocniny vznikol z prvého písmena r latinského slova radix, čo znamená koreň.
U: Dávna predstava odmocniny bola spojená s geometriou, a to konkrétne s obsahom štvorca. Keď matematici chceli vypočítať dĺžku strany štvorca, ktorého obsah je známy (napr. 16 cm²), museli v množine kladných reálnych čísel nájsť koreň rovnice
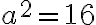 .
.
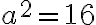 .
. Učiteľov záver
A výsledky by boli dva? Aj
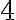 aj
aj 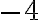 ? Preto sa matematici dohodli, že za výsledok sa vezme len číslo kladné, prípadne nezáporné. Už si môžeme definovať druhú odmocninu.
? Preto sa matematici dohodli, že za výsledok sa vezme len číslo kladné, prípadne nezáporné. Už si môžeme definovať druhú odmocninu.
Majme nezáporné číslo a. Druhou odmocninou z čísla  nazývame také nezáporné číslo
nazývame také nezáporné číslo  , pre ktoré platí:
, pre ktoré platí:
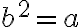
Zapisujeme
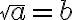
 nazývame také nezáporné číslo
nazývame také nezáporné číslo  , pre ktoré platí:
, pre ktoré platí:
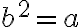
Zapisujeme
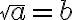
Pri zavádzaní matematických pojmov učiteľ musí mať na zreteli, že takmer celá matematika je založená na historicky overenej dohode a precíznej logike.
Druhá odmocnina II
Metóda priameho prenosu poznatkov (prednáška, opis, vysvetľovanie) Elektronické prípravy - © 2010 Martin Krynický
Tu
Základní škola - 7. ročník
-
Olda učitelům moc nevěří, a proto se hned ptá:
- vždy se snažíme o jednoznačné výsledky (aby se všichni shodli na správném výsledku) ⇒ jednu ze dvou možností zakážeme (raději tu zápornou, abychom se nemuseli starat o znaménka, navíc dluhy stejně nikdo nemá rád)
- druhou odmocninu jsme v geometrii brali jako délku strany čtverce a ta nemůže být záporná.
"Proč neplatí, že
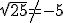 , když
, když 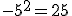 ? Jak to je?"
? Jak to je?"Olda má pravdu, podle všeho, co jsme si dosud říkali, bychom mohli psát i
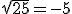 . V matematice však nikdy nepíšeme
. V matematice však nikdy nepíšeme 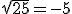 ,
ze dvou základních důvodů:
,
ze dvou základních důvodů:
Ze dvou čísel, jejichž druhá mocnina se rovná 25, bereme za druhou odmocninu pouze
kladné číslo 5. Druhá odmocnina je vždy nezáporné číslo.
Problémy s mocninami s reálnym exponentom
Definícia (Mocnina s prirodzeným exponentom).
Pre každé reálne číslo a prirodzené číslo
a prirodzené číslo  je:
Zápis
je:
Zápis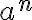 čítame "
čítame " -tá mocnina čísla
-tá mocnina čísla  ". Číslo
". Číslo  nazývame základ mocniny, číslo
nazývame základ mocniny, číslo  nazývame exponent .
nazývame exponent .
Pre každé reálne číslo
 a prirodzené číslo
a prirodzené číslo  je:
Zápis
je:
Zápis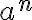 čítame "
čítame " -tá mocnina čísla
-tá mocnina čísla  ". Číslo
". Číslo  nazývame základ mocniny, číslo
nazývame základ mocniny, číslo  nazývame exponent .
nazývame exponent .
Cvičenie.
Pozrite si stránku Online kalkulačka rovníc, nerovníc a systémov.
Pozrite si stránku Online kalkulačka rovníc, nerovníc a systémov.
Vlastnosti.
-
Pre mocninu
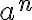 s exponentom
s exponentom 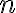 , ktorým je záporné celé číslo platí: ( a^n= \frac{1}{a^ {-n}} \).
, ktorým je záporné celé číslo platí: ( a^n= \frac{1}{a^ {-n}} \). -
Nech
 je kladné reálne číslo a nech
je kladné reálne číslo a nech 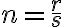 je racionálny exponent, kde
je racionálny exponent, kde  je celé číslo a
je celé číslo a 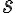 je kladné celé číslo.
Potom je možné robiť úpravy typu
je kladné celé číslo.
Potom je možné robiť úpravy typu
-
Pre
 záporné reálne číslo a racionálny exponent
záporné reálne číslo a racionálny exponent 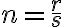 , nie je možné použiť predchádzajúcu úpravu. Pozri cvičenie 2.
, nie je možné použiť predchádzajúcu úpravu. Pozri cvičenie 2.
Definícia (Binomická rovnica).
Binomická rovnica s neznámou je rovnica v tvare
je rovnica v tvare 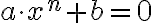 , kde
, kde 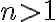 je prirodzené číslo a
je prirodzené číslo a 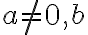 sú komplexné čísla.
sú komplexné čísla.
Binomická rovnica s neznámou
 je rovnica v tvare
je rovnica v tvare 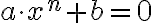 , kde
, kde 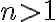 je prirodzené číslo a
je prirodzené číslo a 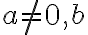 sú komplexné čísla.
sú komplexné čísla.
Základná veta algebry hovorí, že každý polynóm stupňa aspoň prvého s komplexnými koeficientami má v telese komplexných čísel aspoň jeden koreň.
Diskusia k riešeniu binomických rovníc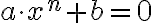 .
.
Zo základnej vety algebry vyplýva, že táto rovnica má práve riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
Každú binomickú rovnicu môžeme upraviť na normovaný tvar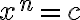 . My sa budeme venovať len binomickým rovniciam, v ktorých
. My sa budeme venovať len binomickým rovniciam, v ktorých  je reálne číslo. Naviac sa zameriame na riešenie rovníc
je reálne číslo. Naviac sa zameriame na riešenie rovníc 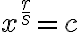 , v ktorých exponent
, v ktorých exponent 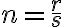 je racionálne číslo.
V tomto prípade rovnicu
je racionálne číslo.
V tomto prípade rovnicu 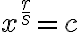 najskôr transformujeme na normovaný tvar
najskôr transformujeme na normovaný tvar 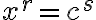 . Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
. Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
Diskusia k riešeniu binomických rovníc
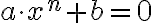 .
.
Zo základnej vety algebry vyplýva, že táto rovnica má práve
 riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
Každú binomickú rovnicu môžeme upraviť na normovaný tvar
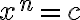 . My sa budeme venovať len binomickým rovniciam, v ktorých
. My sa budeme venovať len binomickým rovniciam, v ktorých  je reálne číslo. Naviac sa zameriame na riešenie rovníc
je reálne číslo. Naviac sa zameriame na riešenie rovníc 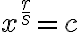 , v ktorých exponent
, v ktorých exponent 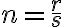 je racionálne číslo.
V tomto prípade rovnicu
je racionálne číslo.
V tomto prípade rovnicu 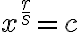 najskôr transformujeme na normovaný tvar
najskôr transformujeme na normovaný tvar 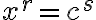 . Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
. Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
- Riešenie prvej rovnice
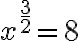 z prvého cvičenia po transformácii na
z prvého cvičenia po transformácii na 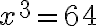 s využitím online kalkulačky:
s využitím online kalkulačky:
 .
. - Riešením druhej rovnice
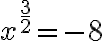 z prvého cvičenia po transformácii na
z prvého cvičenia po transformácii na 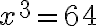
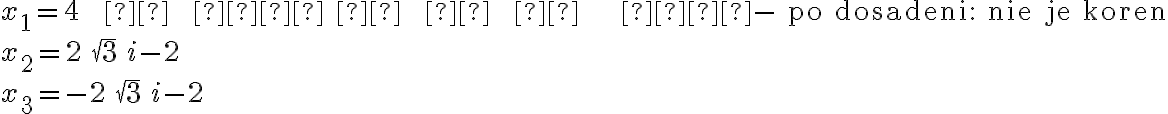
Cvičenie.
Vyriešte rovnicu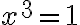 v obore komplexných čísel.
v obore komplexných čísel.
Návod:
Vyjadrite hľadané riešenie v goniometrickom tvare
v goniometrickom tvare 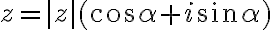 alebo použite vzťah
alebo použite vzťah
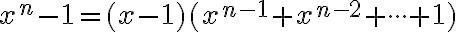 .
.
Vyriešte rovnicu
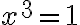 v obore komplexných čísel.
v obore komplexných čísel.
Návod:
Vyjadrite hľadané riešenie
 v goniometrickom tvare
v goniometrickom tvare 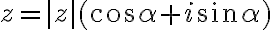 alebo použite vzťah
alebo použite vzťah
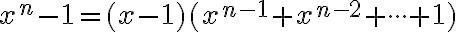 .
.
Pri definovaní pojmu reálne číslo vychádzame z existujúcej množiny racionálnych čísel, ale rozšírenie neurobíme pomocou karteziánskeho súčinu.
Konštrukcia, ktorá "zostrojí" reálne číslo, bude vychádzať z "rezov" na množine racionálnych čísel. Pozrite si kurz Aritmetika Tu.
Konštrukcia, ktorá "zostrojí" reálne číslo, bude vychádzať z "rezov" na množine racionálnych čísel. Pozrite si kurz Aritmetika Tu.
- Termín reálne číslo zaviedol René Descartes (1637) ako spoločný názov pre racionálne a iracionálne čísla.
-
Viac ako dve tisíc rokov sú známe niektoré iracionálne čísla, ktoré sú vyjadrené ako odmocniny (mocniny s racionálnym exponentom) prirodzených čísel
![\sqrt {2}, \sqrt[3]{2} \sqrt {2}, \sqrt[3]{2}](https://lms.umb.sk/filter/tex/pix.php/6d5c677fe326c298cf44e745f38c7e46.png) ...
... -
Euler (1737) dokázal, že číslo
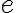 je
iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
je
iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
 je iracionálne.
je iracionálne. - Charles Hermit (1873) ukázal, že číslo
 je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami.
je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami.
Poznámky.
-
Zo strednej školy si možno pamätáte, že
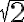 má nekonečný a neperiodický dekadický rozvoj.
má nekonečný a neperiodický dekadický rozvoj. - dokonca niektorí si pamätajú aj niekoľko cifier za desatinnou čiarkou, napr.
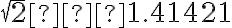
- na stránke Wikipédie môžeme nájsť až 10 miliónov cifier
- vyjadriť
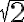 konečným počtom cifier sa nikomu nemôže podariť
konečným počtom cifier sa nikomu nemôže podariť - existuje racionálne číslo, ktoré aproximuje
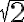 s danou presnosťou.
s danou presnosťou. - Vieme nájsť vhodnú postupnosť racionálnych čísel, ktorej členy sa budú „približovať“ k druhej odmocnine z dvoch.
- Ak vezmeme do úvahy všetky možné konvergentné postupnosti racionálnych čísel, tak ich limity budú zahŕňať aj čísla typu
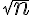 .
. - V nasledujúcich kapitolách popíšeme Dedekindove rezy, pomocou ktorých definujeme reálne čísla.
Dedekindove rezy
Matematik Pytagorovej školy Hippasus (5. stor. pred n. l.) ukázal, že uhlopriečka štvorca s jednotkovou stranou nemôže byť vyjadrená racionálnym číslom1)
Hippasus pravdepodobne dospel k záveru, že
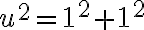 a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi
a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi 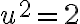 .
.
Tvrdenie.
S využitím vlastností deliteľnosti ukážeme, že táto rovnica nemá v obore racionálnych čísel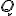 riešenie.
riešenie.
S využitím vlastností deliteľnosti ukážeme, že táto rovnica nemá v obore racionálnych čísel
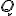 riešenie.
riešenie.
Dokážeme to nepriamo.
Nech existuje racionálne číslo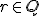 , ktoré je riešením rovnice
, ktoré je riešením rovnice 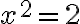 . Potom zrejme
. Potom zrejme 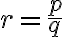 , pričom celé čísla
, pričom celé čísla  sú nesúdeliteľné.
Najväčší spoločný deliteľ čísel
sú nesúdeliteľné.
Najväčší spoločný deliteľ čísel  je rovný
je rovný 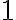 .
.
Po dosadení do rovnice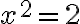 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť 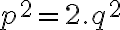 . Na pravej strane rovnosti je určite číslo párne.
Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne.
Z vlastností deliteľnosti celých čísel vyplýva, že číslo 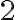 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti.
Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti.
Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá mocnina nepárneho čísla je nepárne číslo. Teda číslo 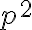 je párne,
preto musí byť aj číslo
je párne,
preto musí byť aj číslo  párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare 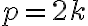 . Po dosadení do rovnosti
. Po dosadení do rovnosti 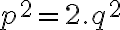 dostávame
dostávame
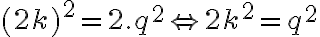 .
.
Analogickou úvahou zistíme, že číslo je párne. Keďže aj číslo
je párne. Keďže aj číslo  je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel 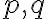 je väčší alebo rovný číslu
je väčší alebo rovný číslu 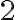 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo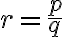 , kde
, kde  sú nesúdeliteľné celé čísla.
Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla.
Pozrite si zápis dôkazu v GeoGebre Tu.
Nech existuje racionálne číslo
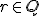 , ktoré je riešením rovnice
, ktoré je riešením rovnice 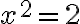 . Potom zrejme
. Potom zrejme 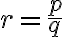 , pričom celé čísla
, pričom celé čísla  sú nesúdeliteľné.
Najväčší spoločný deliteľ čísel
sú nesúdeliteľné.
Najväčší spoločný deliteľ čísel  je rovný
je rovný 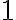 .
.
Po dosadení do rovnice
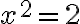 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť 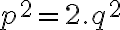 . Na pravej strane rovnosti je určite číslo párne.
Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne.
Z vlastností deliteľnosti celých čísel vyplýva, že číslo 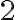 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti.
Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti.
Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá mocnina nepárneho čísla je nepárne číslo. Teda číslo 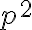 je párne,
preto musí byť aj číslo
je párne,
preto musí byť aj číslo  párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare 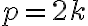 . Po dosadení do rovnosti
. Po dosadení do rovnosti 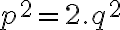 dostávame
dostávame
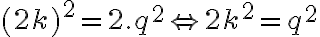 .
.
Analogickou úvahou zistíme, že číslo
 je párne. Keďže aj číslo
je párne. Keďže aj číslo  je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel 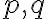 je väčší alebo rovný číslu
je väčší alebo rovný číslu 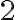 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo
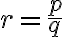 , kde
, kde  sú nesúdeliteľné celé čísla.
Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla.
Pozrite si zápis dôkazu v GeoGebre Tu.
Poznámka.
Ak označíme jedno riešenie rovnice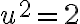 symbolom
symbolom
![\sqrt[]{2} \sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/297a1f700540ffde5fd6e4874d969d54.png) (druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj
(druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj ![-\sqrt[]{2} -\sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/98c948e1f301c9a76f2fb05d26057d97.png) je riešením rovnice
je riešením rovnice
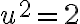 a tiež nie je racionálne.
a tiež nie je racionálne.
Ak označíme jedno riešenie rovnice
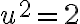 symbolom
symbolom
![\sqrt[]{2} \sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/297a1f700540ffde5fd6e4874d969d54.png) (druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj
(druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj ![-\sqrt[]{2} -\sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/98c948e1f301c9a76f2fb05d26057d97.png) je riešením rovnice
je riešením rovnice
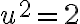 a tiež nie je racionálne.
a tiež nie je racionálne.
Cvičenie.
Zapíšte dôkaz ... v GeoGebre.
Zapíšte dôkaz ... v GeoGebre.
Reálne čísla zavádzame pomocou Dedekindových rezov na množine racionálnych čísel.
Podmnožinu
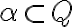 nazývame Dedekindovým rezom množiny
nazývame Dedekindovým rezom množiny
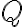 , ak
, ak

Dolná časť nemá najväčší prvok.
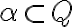 nazývame Dedekindovým rezom množiny
nazývame Dedekindovým rezom množiny
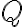 , ak
, ak
- podmnožina
 je neprázdna množina:
je neprázdna množina:
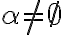
- doplnok
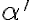 podmnožiny
podmnožiny
 v množine
v množine
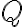 je tiež neprázdny:
je tiež neprázdny:
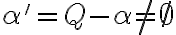 .
. - Nech
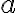 je prvkom rezu
je prvkom rezu
 a nech
a nech
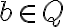 má vlastnosť
má vlastnosť
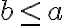 . Potom musí aj racionálne číslo
. Potom musí aj racionálne číslo
 patriť do rezu:
patriť do rezu:
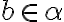 .
. - Rez
 nemá najväčší prvok. Ak
nemá najväčší prvok. Ak
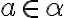 , tak existuje
, tak existuje
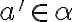 , pre ktoré je
, pre ktoré je
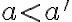 .
.
Dolná časť nemá najväčší prvok.
Definícia
Množinu všetkých rezov množiny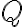 označíme symbolom
označíme symbolom
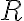 . Prvky patriace do množiny
. Prvky patriace do množiny
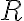 nazývame reálne čísla.
nazývame reálne čísla.
Množinu všetkých rezov množiny
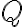 označíme symbolom
označíme symbolom
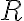 . Prvky patriace do množiny
. Prvky patriace do množiny
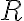 nazývame reálne čísla.
nazývame reálne čísla.
Množinu reálnych čísel sme vytvorili pomocou už známej množiny racionálnych čísel. Proces tvorby sa opiera o podmnožiny
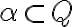 , ktoré majú predpísané štyri vlastnosti.
, ktoré majú predpísané štyri vlastnosti.
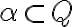 , ktoré majú predpísané štyri vlastnosti.
, ktoré majú predpísané štyri vlastnosti.
-
Prvé dve vlastnosti hovoria, že za podmnožinu
 nemôžeme vziať prázdnu množinu ani množinu všetkých racionálnych čísel.
nemôžeme vziať prázdnu množinu ani množinu všetkých racionálnych čísel. -
Tretia vlastnosť požaduje, aby podmnožina
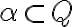 bola „slušne“ usporiadaná:
bola „slušne“ usporiadaná: - ak podmnožina
 obsahuje racionálne číslo
obsahuje racionálne číslo
 , tak táto podmnožina musí obsahovať aj všetky racionálne čísla menšie od čísla
, tak táto podmnožina musí obsahovať aj všetky racionálne čísla menšie od čísla

- ak by sme na číselnej osi zobrazili bod
 reprezentujúci racionálne číslo
reprezentujúci racionálne číslo
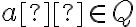 , tak podmnožina
, tak podmnožina
 musí obsahovať polpriamku smerujúcu doľava od bodu
musí obsahovať polpriamku smerujúcu doľava od bodu
 .
.
-
Štvrtú vlastnosť si môžeme interpretovať ako podmnožinu
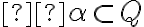 , ktorá zodpovedá sprava otvorenému intervalu
, ktorá zodpovedá sprava otvorenému intervalu 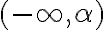 .
. - Reálne čísla, ktoré nie sú racionálne budeme nazývať iracionálne čísla
Vlastnosti rezov
- Dedekindove rezy, ktorých horná časť má najmenší prvok predstavujú racionálne číslo.
- Nech
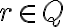 je ľubovoľné ale pevne zvolené racionálne číslo, potom podmnožina
je ľubovoľné ale pevne zvolené racionálne číslo, potom podmnožina
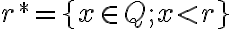 je rezom. Dokážte to.
je rezom. Dokážte to. - Podmnožina
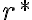 reprezentuje racionálne číslo
reprezentuje racionálne číslo

- množina
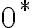 je tiež Dedekindov rez, ktorý (ako neskôr ukážeme) má vlastnosť neutrálneho prvku vzhľadom na sčítanie.
je tiež Dedekindov rez, ktorý (ako neskôr ukážeme) má vlastnosť neutrálneho prvku vzhľadom na sčítanie. - ukážte, že zobrazenie
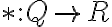 je injektívne.
je injektívne.
- V bode 2. zameňte výrokovú formu
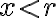 za
za
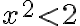 . Dostanete rez
. Dostanete rez
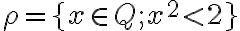 , ktorý reprezentuje iracionálne číslo
, ktorý reprezentuje iracionálne číslo 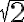 .
.
__________________________________________________________________________________________
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
Seminárne zadania
Úloha
Pokúste sa odvodiť vzorec pre výpočet - tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice
- tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice 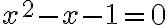 . Pozrite si prezentáciu Fibonacciho postupnosť Tu.
. Pozrite si prezentáciu Fibonacciho postupnosť Tu.
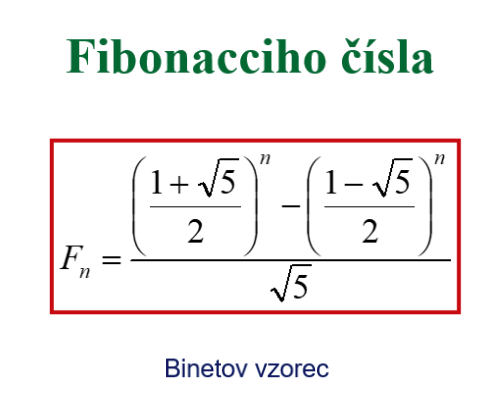
Pokúste sa odvodiť vzorec pre výpočet
 - tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice
- tého člena Fibonacciho postupnosti. Pri jeho odvodení využite riešenie kvadratickej rovnice 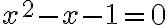 . Pozrite si prezentáciu Fibonacciho postupnosť Tu.
. Pozrite si prezentáciu Fibonacciho postupnosť Tu.
V nasledujúcich úlohách číslo  je prirodzené číslo:
je prirodzené číslo: 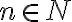 . Experimentovaním sa pokúste nájsť vzorec (formulu) pre výpočet súčtu prvých
. Experimentovaním sa pokúste nájsť vzorec (formulu) pre výpočet súčtu prvých  členov postupnosti.
členov postupnosti.
 je prirodzené číslo:
je prirodzené číslo: 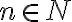 . Experimentovaním sa pokúste nájsť vzorec (formulu) pre výpočet súčtu prvých
. Experimentovaním sa pokúste nájsť vzorec (formulu) pre výpočet súčtu prvých  členov postupnosti.
členov postupnosti.Úlohy
- Nájdite vzorec pre súčet
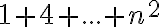 .
.
-
Spočítajte
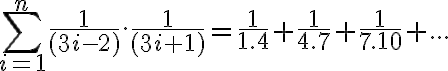 .
. - Postupnosť je daná predpisom
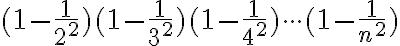 .
.
Vypočítajte hodnotu tohto súčinu pre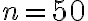 . Pozri Tu.
. Pozri Tu.
Zadanie (seminárne).
Vyberte si minimálne 3 úlohy zo súboru 54 netradičných úloh z matematiky z práce1), ktoré spracujte vo forme prezentácie.
Vyberte si minimálne 3 úlohy zo súboru 54 netradičných úloh z matematiky z práce1), ktoré spracujte vo forme prezentácie.
Svoje prezentácie doplňte
metodickými resp. historickými poznámkami tak, aby boli vhodné pre učiteľov matematiky na 2. stupni ZŠ.
a osemročných gymnáziách.
___________________________________________________________________________
1) Somorčík, A.: Paradoxy a provokácie vo vyučovaní matematiky. Osvedčená pdagogická skúsenosť edukačnej praxe, MPC Bratislava 2012. Dostupné Tu
1) Somorčík, A.: Paradoxy a provokácie vo vyučovaní matematiky. Osvedčená pdagogická skúsenosť edukačnej praxe, MPC Bratislava 2012. Dostupné Tu

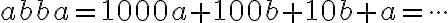


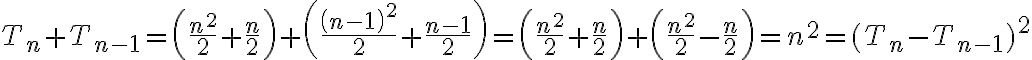
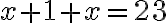
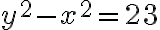
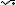
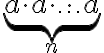
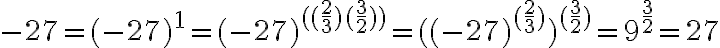
![a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r](https://lms.umb.sk/filter/tex/pix.php/3e7b97dda331b0af77ba047a99702a02.png)