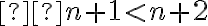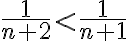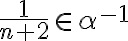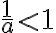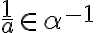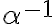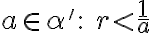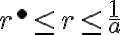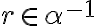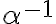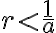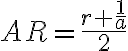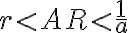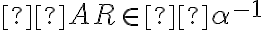Reálne a komplexné čísla
Reálne a komplexné čísla
Dedekindove rezy
Vlastnosti rezov
Dokážte tvrdenia
- Nech
 je kladný rez na množine racionálnych čísel. Potom podmnožina
je kladný rez na množine racionálnych čísel. Potom podmnožina
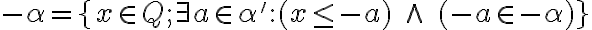 je Dedekindov rez.
je Dedekindov rez. -
Nech
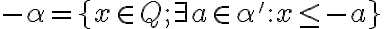 a nech
a nech
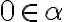 .
.
- Najskôr ukážeme, že platí prvá vlastnosť pre rezy:
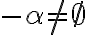 . Nech
. Nech
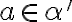 je racionálne číslo. Zrejme platí
je racionálne číslo. Zrejme platí
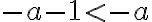 ,
,
odkiaľ dostávame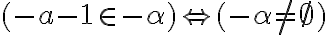 .
.
- Druhú vlastnosť budeme dokazovať nepriamo. Predpokladajme sporom, že
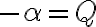 .
.
Pre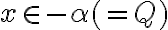 bude aj
bude aj
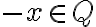 . Z definície
. Z definície
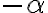 dostávame, že existuje
dostávame, že existuje
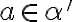 také, že
také, že
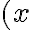 .
.
Pretože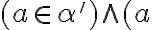
musí tiež platiť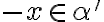
Týmto sme ukázali, že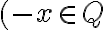
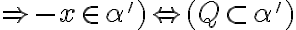
odkiaľ dostávame, že (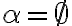 \), čo je spor.
\), čo je spor. - Tretia vlastnosť:
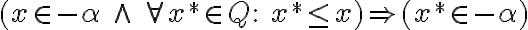 .
.
Z definície rezu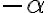 vyplýva, že existuje
vyplýva, že existuje
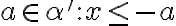 . Zrejme platia nerovnosti:
. Zrejme platia nerovnosti:
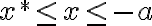 ,
,
odkiaľ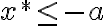 ,
,
preto platí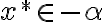 .
.
(interpretujte túto situáciu v applete). - Štvrtá vlastnosť: rez
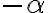 nemá najväčší prvok. Nepriamo: nech
nemá najväčší prvok. Nepriamo: nech
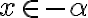
je najväčší prvok. Z definície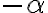 dostávame, že existuje
dostávame, že existuje
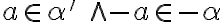 také, že
také, že
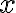 ,
,
čo je spor s vlastnosťou "byť najväčší".
- Najskôr ukážeme, že platí prvá vlastnosť pre rezy:
- Pre ľubovoľný kladný rez
 platí:
platí: 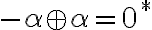 .
Dôkaz
.
Dôkaz
- Nech
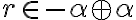 , potom existujú racionálne čísla
, potom existujú racionálne čísla
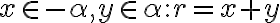 . Z definície rezu
. Z definície rezu
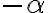 dostávame, že existuje racionálne číslo
dostávame, že existuje racionálne číslo
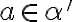 , pre ktoré je
, pre ktoré je
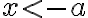 .
.
Keďže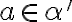 a
a
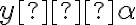 , tak musí platiť
, tak musí platiť 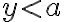 . Zvoľte si v applete body
. Zvoľte si v applete body
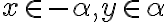 tak, aby spĺňali tieto podmienky.
tak, aby spĺňali tieto podmienky.
Z monotónnosti sčítania dostaneme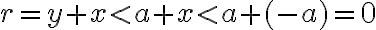
Z poslednej nerovnosti vyplýva, že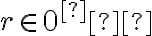 ,
,
preto platí množinová inklúzia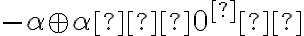 .
.
- Ak
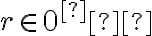 , tak musíme nájsť dve racionálne čísla
, tak musíme nájsť dve racionálne čísla
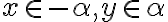 , pre ktoré bude platiť:
, pre ktoré bude platiť:
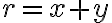 . Predpokladajme, že také dve racionálne čísla
. Predpokladajme, že také dve racionálne čísla
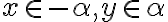 existujú. Potom z definície rezu
existujú. Potom z definície rezu
 vyplýva, že
vyplýva, že
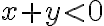 .
.
Pre racionálne číslo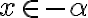 musí existovať
musí existovať
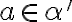 , pričom platí
, pričom platí 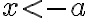 . Po jednoduchej úprave dostaneme
. Po jednoduchej úprave dostaneme
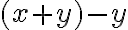 .
.
Predchádzajúca nerovnosť hovorí, že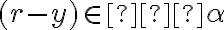 . Zároveň vidíme, že
. Zároveň vidíme, že
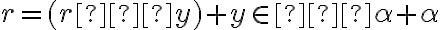 .
.
Záver: Ak existujú dve racionálne čísla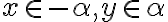 s požadovanou vlastnosťou, tak platí
s požadovanou vlastnosťou, tak platí
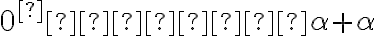 .
. - Nech
 je kladný rez. Potom podmnožina
je kladný rez. Potom podmnožina
 , kde
, kde
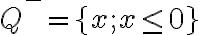 je tiež Dedekindov rez
je tiež Dedekindov rez - Pre ľubovoľný kladný rez
 platí:
platí: 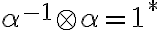 .
Dôkaz
.
Dôkaz
-
Nech
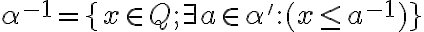 .
.
- Ukážeme, že
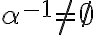 . Uvažujme dva prípady
. Uvažujme dva prípady
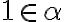 a
a
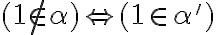 .
. - v prvom prípade existuje prirodzené číslo
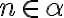 ale
ale
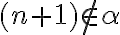 teda patrí do doplnku
teda patrí do doplnku
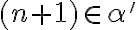
- v druhom prípade
![[1 \in \alpha'] [1 \in \alpha']](https://lms.umb.sk/filter/tex/pix.php/009ada447a4fb25e9c97ef64aa3bd830.png) určite existuje číslo
určite existuje číslo
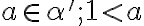 ,
V oboch prípadoch (i. aj ii.) je
,
V oboch prípadoch (i. aj ii.) je - Pri dôkaze druhej vlastnosti rezov
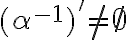 môžeme postupovať opäť tak, že dôkaz rozdelíme do dvoch častí:
môžeme postupovať opäť tak, že dôkaz rozdelíme do dvoch častí:
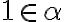 a
a
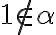 .
.
Načrtnite tieto situácie v applete. - Nech
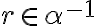 a nech
a nech
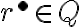 má vlastnosť
má vlastnosť
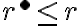 . Potom aj racionálne číslo
. Potom aj racionálne číslo
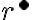 patrí do rezu:
patrí do rezu:
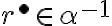 .
. - Rez
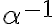 nemá najväčší prvok. Dokážeme nepriamo:
nemá najväčší prvok. Dokážeme nepriamo: - Nastavte obrázok ...
- dôkaz je podobný
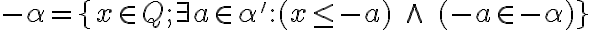 nie je nutná podmienka
nie je nutná podmienka 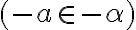 . Dá sa dokázať, že prvok
. Dá sa dokázať, že prvok
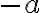 je prvkom rezu
je prvkom rezu
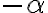 .
.
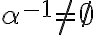 .
.
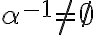 obsahuje aspoň jedno kladné racionálne čéslo, tak obsahuje aj všetky záporné racionálne čísla (prečo?).
obsahuje aspoň jedno kladné racionálne čéslo, tak obsahuje aj všetky záporné racionálne čísla (prečo?).