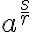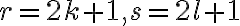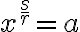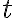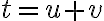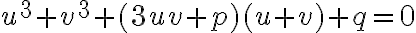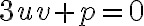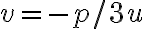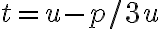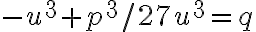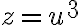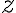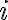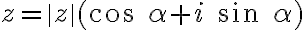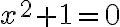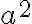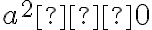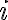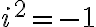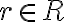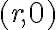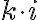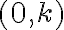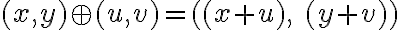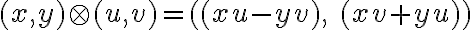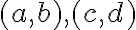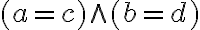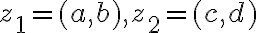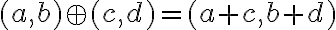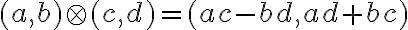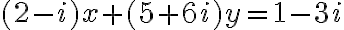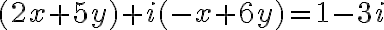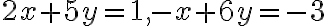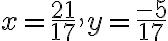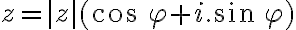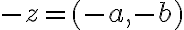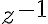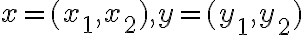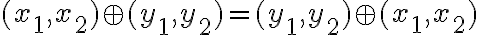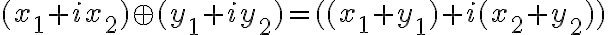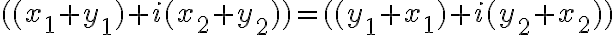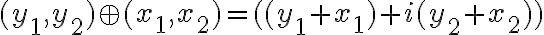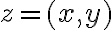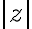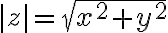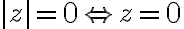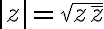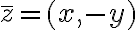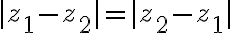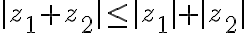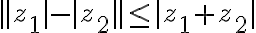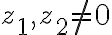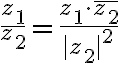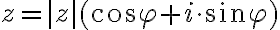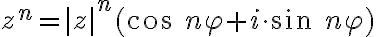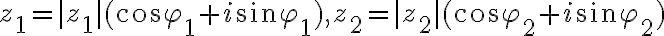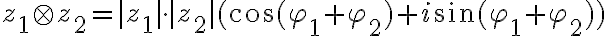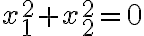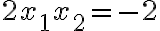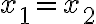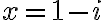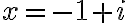Reálne a komplexné čísla
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Reálne a komplexné čísla |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:33 |
Opis
Reálne a komplexné čísla
Množina reálnych čísel
Pri definovaní pojmu reálne číslo vychádzame z existujúcej množiny racionálnych čísel, ale rozšírenie neurobíme pomocou karteziánskeho súčinu.
Konštrukcia, ktorá popíše reálne číslo vychádza z "rezov" na množine racionálnych čísel.
Konštrukcia, ktorá popíše reálne číslo vychádza z "rezov" na množine racionálnych čísel.
- Termín reálne číslo zaviedol René Descartes (1637) ako spoločný názov pre racionálne a iracionálne čísla.
-
V staroveku už boli známe iracionálne čísla ako odmocniny niektorých prirodzených čísel
![\sqrt {2}, \sqrt[3]{2} \sqrt {2}, \sqrt[3]{2}](https://lms.umb.sk/filter/tex/pix.php/6d5c677fe326c298cf44e745f38c7e46.png) .
. -
Euler (1737) dokázal, že číslo
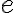 je
iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
je
iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
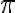 je iracionálne.
je iracionálne. - Charles Hermit (1873) ukázal, že číslo
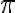 je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami.
je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami.
-
Zo strednej školy si možno pamätáte, že
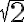 má nekonečný a neperiodický dekadický rozvoj.
má nekonečný a neperiodický dekadický rozvoj. - dokonca niektorí si pamätajú aj niekoľko cifier za desatinnou čiarkou, napr.
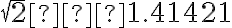
- na stránke Wikipédie môžeme nájsť až 10 miliónov cifier
- vyjadriť
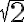 konečným počtom cifier sa nikomu nemôže podariť
konečným počtom cifier sa nikomu nemôže podariť - existuje racionálne číslo, ktoré aproximuje
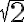 s danou presnosťou.
s danou presnosťou. - Vieme nájsť vhodnú postupnosť racionálnych čísel, ktorej členy sa budú „približovať“ k druhej odmocnine z dvoch.
- Ak vezmeme do úvahy všetky možné konvergentné postupnosti racionálnych čísel, tak ich limity budú zahŕňať aj čísla typu
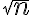 .
. - V nasledujúcich kapitolách popíšeme dedekindove rezy, pomocou ktorých definujeme reálne čísla.
Pytagorova škola
Matematik Pytagorovej školy Hippasus (5. stor. pred n. l.) ukázal, že uhlopriečka štvorca s jednotkovou stranou nemôže byť vyjadrená racionálnym číslom1)
Hippasus pravdepodobne dospel k záveru, že
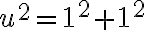 a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi
a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi 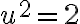 .
.
S využitím vlastností deliteľnosti ukážeme, že táto rovnica nemá v obore racionálnych čísel
 riešenie.
riešenie.
 riešenie.
riešenie.
Dôkaz.
Nech existuje racionálne číslo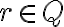 , ktoré je riešením rovnice
, ktoré je riešením rovnice 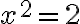 . Potom zrejme
. Potom zrejme
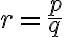 , pričom celé čísla
, pričom celé čísla
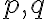 sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
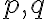 je rovný
je rovný
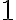 .
.
Po dosadení do rovnice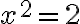 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť
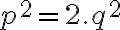 . Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
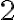 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
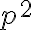 je párne, preto musí byť aj číslo
je párne, preto musí byť aj číslo
 párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare
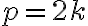 . Po dosadení do rovnosti
. Po dosadení do rovnosti
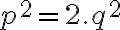 dostávame
dostávame
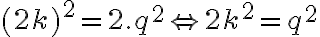 .
.
Analogickou úvahou zistíme, že číslo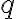 je párne. Keďže aj číslo
je párne. Keďže aj číslo
 je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel
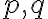 je väčší alebo rovný číslu
je väčší alebo rovný číslu
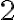 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo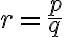 , kde
, kde
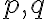 sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
Nech existuje racionálne číslo
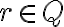 , ktoré je riešením rovnice
, ktoré je riešením rovnice 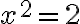 . Potom zrejme
. Potom zrejme
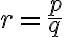 , pričom celé čísla
, pričom celé čísla
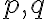 sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
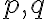 je rovný
je rovný
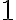 .
.
Po dosadení do rovnice
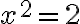 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť
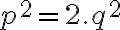 . Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
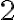 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
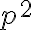 je párne, preto musí byť aj číslo
je párne, preto musí byť aj číslo
 párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare
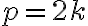 . Po dosadení do rovnosti
. Po dosadení do rovnosti
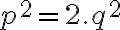 dostávame
dostávame
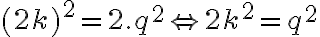 .
.
Analogickou úvahou zistíme, že číslo
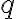 je párne. Keďže aj číslo
je párne. Keďže aj číslo
 je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel
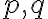 je väčší alebo rovný číslu
je väčší alebo rovný číslu
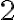 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo
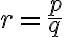 , kde
, kde
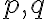 sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
Ak označíme jedno riešenie rovnice
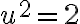 symbolom
symbolom
![\sqrt[]{2} \sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/297a1f700540ffde5fd6e4874d969d54.png) (druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj
(druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj
![-\sqrt[]{2} -\sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/98c948e1f301c9a76f2fb05d26057d97.png) je riešením rovnice
je riešením rovnice
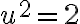 a tiež nie je racionálne.
a tiež nie je racionálne.
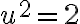 symbolom
symbolom
![\sqrt[]{2} \sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/297a1f700540ffde5fd6e4874d969d54.png) (druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj
(druhá odmocnina z dvoch), tak toto číslo nie je racionálne číslo. Zrejme aj
![-\sqrt[]{2} -\sqrt[]{2}](https://lms.umb.sk/filter/tex/pix.php/98c948e1f301c9a76f2fb05d26057d97.png) je riešením rovnice
je riešením rovnice
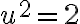 a tiež nie je racionálne.
a tiež nie je racionálne.
___________________________________________________________________________________________
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
Dedekindove rezy
Reálne čísla zavedieme pomocou Dedekindových rezov na množine racionálnych čísel.
Podmnožinu
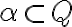 nazývame Dedekindovým rezom množiny
nazývame Dedekindovým rezom množiny
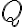 , ak
, ak

Dolná časť nemá najväčší prvok.
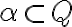 nazývame Dedekindovým rezom množiny
nazývame Dedekindovým rezom množiny
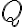 , ak
, ak
- podmnožina
 je neprázdna množina:
je neprázdna množina:
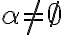
- doplnok
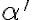 podmnožiny
podmnožiny
 v množine
v množine
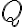 je tiež neprázdny:
je tiež neprázdny:
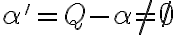 .
. - Nech
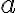 je prvkom rezu
je prvkom rezu
 a nech
a nech
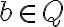 má vlastnosť
má vlastnosť
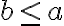 . Potom musí aj racionálne číslo
. Potom musí aj racionálne číslo
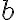 patriť do rezu:
patriť do rezu:
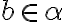 .
. - Rez
 nemá najväčší prvok. Ak
nemá najväčší prvok. Ak
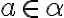 , tak existuje
, tak existuje
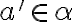 , pre ktoré je
, pre ktoré je
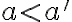 .
.
Dolná časť nemá najväčší prvok.
Definícia.
Množinu všetkých rezov množiny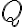 označíme symbolom
označíme symbolom
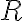 . Prvky patriace do množiny
. Prvky patriace do množiny
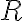 nazývame reálne čísla.
nazývame reálne čísla.
Množinu všetkých rezov množiny
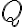 označíme symbolom
označíme symbolom
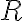 . Prvky patriace do množiny
. Prvky patriace do množiny
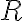 nazývame reálne čísla.
nazývame reálne čísla.
Množinu reálnych čísel sme vytvorili pomocou už známej množiny racionálnych čísel. Proces tvorby sa opiera o podmnožiny
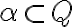 , ktoré majú predpísané štyri vlastnosti.
, ktoré majú predpísané štyri vlastnosti.
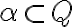 , ktoré majú predpísané štyri vlastnosti.
, ktoré majú predpísané štyri vlastnosti.
-
Prvé dve vlastnosti hovoria, že za podmnožinu
 nemôžeme vziať prázdnu množinu ani množinu všetkých racionálnych čísel.
nemôžeme vziať prázdnu množinu ani množinu všetkých racionálnych čísel. -
Tretia vlastnosť požaduje, aby podmnožina
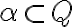 bola „slušne“ usporiadaná:
bola „slušne“ usporiadaná: - ak podmnožina
 obsahuje racionálne číslo
obsahuje racionálne číslo
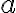 , tak táto podmnožina musí obsahovať aj všetky racionálne čísla menšie od čísla
, tak táto podmnožina musí obsahovať aj všetky racionálne čísla menšie od čísla
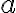
- ak by sme na číselnej osi zobrazili bod
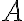 reprezentujúci racionálne číslo
reprezentujúci racionálne číslo
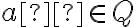 , tak podmnožina
, tak podmnožina
 musí obsahovať polpriamku smerujúcu doľava od bodu
musí obsahovať polpriamku smerujúcu doľava od bodu
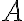 .
.
-
Štvrtú vlastnosť si môžeme interpretovať ako podmnožinu
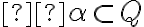 , ktorá zodpovedá sprava otvorenému intervalu
, ktorá zodpovedá sprava otvorenému intervalu 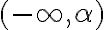 .
. - Reálne čísla, ktoré nie sú racionálne budeme nazývať iracionálne čísla
Vlastnosti rezov.
- Dedekindove rezy, ktorých horná časť má najmenší prvok predstavujú racionálne číslo.
- Nech
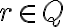 je ľubovoľné ale pevne zvolené racionálne číslo, potom podmnožina
je ľubovoľné ale pevne zvolené racionálne číslo, potom podmnožina
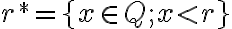 je rezom. Dokážte to.
je rezom. Dokážte to. - Podmnožina
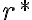 reprezentuje racionálne číslo
reprezentuje racionálne číslo

- množina
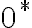 je tiež Dedekindov rez, ktorý (ako neskôr ukážeme) má vlastnosť neutrálneho prvku vzhľadom na sčítanie.
je tiež Dedekindov rez, ktorý (ako neskôr ukážeme) má vlastnosť neutrálneho prvku vzhľadom na sčítanie. - ukážte, že zobrazenie
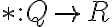 je injektívne.
je injektívne.
- V bode 2. zameňte výrokovú formu
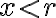 za
za
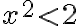 . Dostanete rez
. Dostanete rez
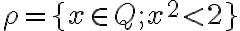 , ktorý reprezentuje iracionálne číslo
, ktorý reprezentuje iracionálne číslo 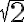 .
.
Súčet reálnych čísel
Nech
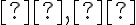 sú dva rezy na množine racionálnych čísel:
sú dva rezy na množine racionálnych čísel:
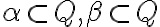 . V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
. V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
 sú dva rezy na množine racionálnych čísel:
sú dva rezy na množine racionálnych čísel:
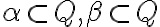 . V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
. V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
Vytvorme množinu
 všetkých možných (racionálnych) súčtov
všetkých možných (racionálnych) súčtov
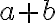 , kde
, kde
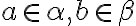 sú racionálne čísla.
sú racionálne čísla.
- Množiny
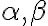 sú neprázdne, preto existujú prvky
sú neprázdne, preto existujú prvky
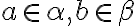 . Množina
. Množina
 je neprázdna, lebo obsahuje racionálne číslo
je neprázdna, lebo obsahuje racionálne číslo
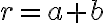 .
. - Ukážeme, že množina
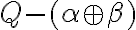 je neprázdna. Množiny
je neprázdna. Množiny
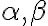 sú rezmi, preto existujú prvky
sú rezmi, preto existujú prvky
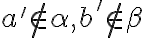 Zrejme pre ľubovoľné prvky
Zrejme pre ľubovoľné prvky
- Nech
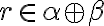 , potom platí
, potom platí
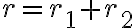 , kde
, kde
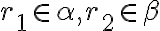 . Nech
. Nech
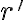 je racionálne číslo, pre ktoré platí
je racionálne číslo, pre ktoré platí
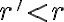 (resp.
(resp.
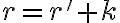 ). Po dosadení dostaneme
). Po dosadení dostaneme
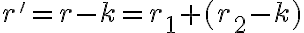 ,
,
čo znamená, že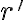 je súčtom dvoch racionálnych čísel.
je súčtom dvoch racionálnych čísel. - Množina
 nemá najväčší prvok. V opačnom prípade, ak by
nemá najväčší prvok. V opačnom prípade, ak by
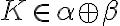 bol najväčší prvok, tak musia existovať dve racionálne čísla
bol najväčší prvok, tak musia existovať dve racionálne čísla
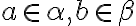 , pričom
, pričom
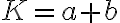 . Bez ujmy na všeobecnosti predpokladajme, že
. Bez ujmy na všeobecnosti predpokladajme, že
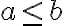 .
.
Keďže je tiež rez, tak nemá najväčší prvok. Musí existovať racionálne číslo
je tiež rez, tak nemá najväčší prvok. Musí existovať racionálne číslo
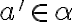 s vlastnosťou
s vlastnosťou
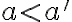 . Relácia
. Relácia
 je monotónna, preto
je monotónna, preto
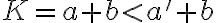 ,
čo je spor s predpokladom, že
,
čo je spor s predpokladom, že
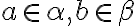 platí
platí
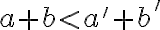 .
.
To znamená, že
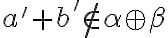 , odkiaľ dostávame, že
, odkiaľ dostávame, že
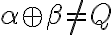 .
.
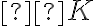 je najväčším prvkom. Tieto tvrdenia nás oprávňujú definovať súčet reálnych ako súčet dedekindových rezov.
je najväčším prvkom. Tieto tvrdenia nás oprávňujú definovať súčet reálnych ako súčet dedekindových rezov.
Definícia
Majme Dedekindove rezy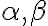 na množine racionálnych čísel. Množinu
na množine racionálnych čísel. Množinu
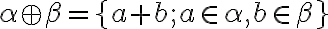 nazveme súčtom reálnych čísel.
nazveme súčtom reálnych čísel.
Majme Dedekindove rezy
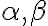 na množine racionálnych čísel. Množinu
na množine racionálnych čísel. Množinu
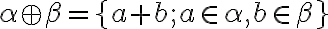 nazveme súčtom reálnych čísel.
nazveme súčtom reálnych čísel.
Súčin reálnych čísel
Operáciu násobenia dvoch reálnych čísel zavedieme pomocou súčinu kladných Dedekindových rezov.
Definícia
-
Rez
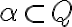 nazveme
kladným Dedekindových rezom, ak dolná časť rezu obsahuje aspoň jedno kladné racionálne číslo:
nazveme
kladným Dedekindových rezom, ak dolná časť rezu obsahuje aspoň jedno kladné racionálne číslo:
 je kladný
je kladný
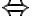
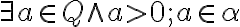 .
. - Množinu všetkých kladných rezov označíme symbolom
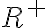 .
.
- ak
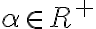 je kladný rez, potom
je kladný rez, potom
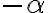 nazývame záporný rez
nazývame záporný rez - rez
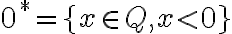 nazývame nulový rez.
nazývame nulový rez.
- množinu všetkých záporných rezov označíme symbolom
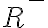 .
.
-
Pre kladné rezy
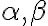 zaveďme súčin kladných rezov:
zaveďme súčin kladných rezov:
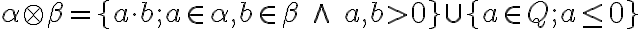 .
.
vytvárame všetky možné súčiny kladných racionálnych čísel z obidvoch rezov, ku ktorým pridáme všetky záporné racionálne čísla vrátane nuly.
K vlastnostiam súčinu viac nájdete v práci: Michal Botur: UVOD DO ARITMETIKY
Vlastnosti rezov
Dokážte tvrdenia- Nech
 je kladný rez na množine racionálnych čísel. Potom podmnožina
je kladný rez na množine racionálnych čísel. Potom podmnožina
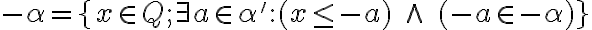 je Dedekindov rez.
je Dedekindov rez. -
Nech
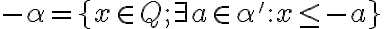 a nech
a nech
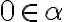 .
.
- Najskôr ukážeme, že platí prvá vlastnosť pre rezy:
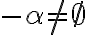 . Nech
. Nech
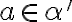 je racionálne číslo. Zrejme platí
je racionálne číslo. Zrejme platí
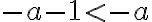 ,
,
odkiaľ dostávame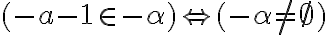 .
.
- Druhú vlastnosť budeme dokazovať nepriamo. Predpokladajme sporom, že
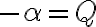 .
.
Pre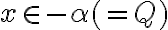 bude aj
bude aj
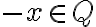 . Z definície
. Z definície
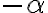 dostávame, že existuje
dostávame, že existuje
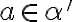 také, že
také, že
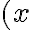 .
.
Pretože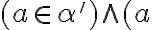
musí tiež platiť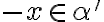
Týmto sme ukázali, že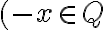
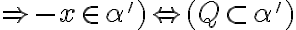
odkiaľ dostávame, že (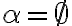 \), čo je spor.
\), čo je spor. - Tretia vlastnosť:
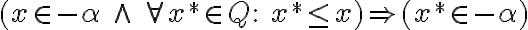 .
.
Z definície rezu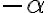 vyplýva, že existuje
vyplýva, že existuje
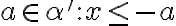 . Zrejme platia nerovnosti:
. Zrejme platia nerovnosti:
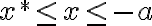 ,
,
odkiaľ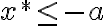 ,
,
preto platí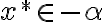 .
.
(interpretujte túto situáciu v applete). - Štvrtá vlastnosť: rez
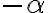 nemá najväčší prvok. Nepriamo: nech
nemá najväčší prvok. Nepriamo: nech
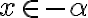
je najväčší prvok. Z definície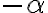 dostávame, že existuje
dostávame, že existuje
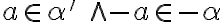 také, že
také, že
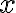 ,
,
čo je spor s vlastnosťou "byť najväčší".
- Najskôr ukážeme, že platí prvá vlastnosť pre rezy:
- Pre ľubovoľný kladný rez
 platí:
platí: 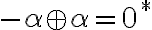 .
Dôkaz
.
Dôkaz
- Nech
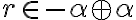 , potom existujú racionálne čísla
, potom existujú racionálne čísla
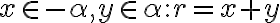 . Z definície rezu
. Z definície rezu
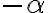 dostávame, že existuje racionálne číslo
dostávame, že existuje racionálne číslo
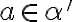 , pre ktoré je
, pre ktoré je
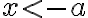 .
.
Keďže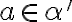 a
a
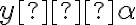 , tak musí platiť
, tak musí platiť 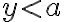 . Zvoľte si v applete body
. Zvoľte si v applete body
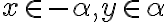 tak, aby spĺňali tieto podmienky.
tak, aby spĺňali tieto podmienky.
Z monotónnosti sčítania dostaneme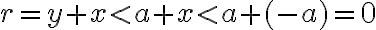
Z poslednej nerovnosti vyplýva, že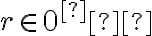 ,
,
preto platí množinová inklúzia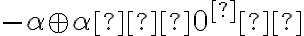 .
.
- Ak
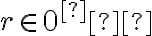 , tak musíme nájsť dve racionálne čísla
, tak musíme nájsť dve racionálne čísla
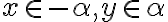 , pre ktoré bude platiť:
, pre ktoré bude platiť:
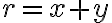 . Predpokladajme, že také dve racionálne čísla
. Predpokladajme, že také dve racionálne čísla
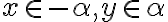 existujú. Potom z definície rezu
existujú. Potom z definície rezu
 vyplýva, že
vyplýva, že
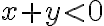 .
.
Pre racionálne číslo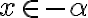 musí existovať
musí existovať
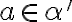 , pričom platí
, pričom platí 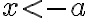 . Po jednoduchej úprave dostaneme
. Po jednoduchej úprave dostaneme
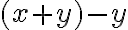 .
.
Predchádzajúca nerovnosť hovorí, že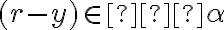 . Zároveň vidíme, že
. Zároveň vidíme, že
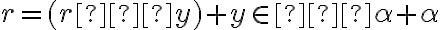 .
.
Záver: Ak existujú dve racionálne čísla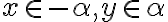 s požadovanou vlastnosťou, tak platí
s požadovanou vlastnosťou, tak platí
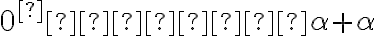 .
. - Nech
 je kladný rez. Potom podmnožina
je kladný rez. Potom podmnožina
 , kde
, kde
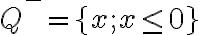 je tiež Dedekindov rez
je tiež Dedekindov rez - Pre ľubovoľný kladný rez
 platí:
platí: 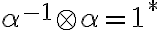 .
Dôkaz
.
Dôkaz
-
Nech
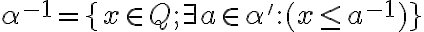 .
.
- Ukážeme, že
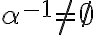 . Uvažujme dva prípady
. Uvažujme dva prípady
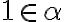 a
a
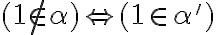 .
. - v prvom prípade existuje prirodzené číslo
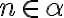 ale
ale
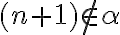 teda patrí do doplnku
teda patrí do doplnku
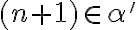
- v druhom prípade
![[1 \in \alpha'] [1 \in \alpha']](https://lms.umb.sk/filter/tex/pix.php/009ada447a4fb25e9c97ef64aa3bd830.png) určite existuje číslo
určite existuje číslo
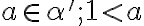 ,
V oboch prípadoch (i. aj ii.) je
,
V oboch prípadoch (i. aj ii.) je - Pri dôkaze druhej vlastnosti rezov
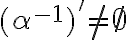 môžeme postupovať opäť tak, že dôkaz rozdelíme do dvoch častí:
môžeme postupovať opäť tak, že dôkaz rozdelíme do dvoch častí:
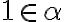 a
a
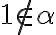 .
.
Načrtnite tieto situácie v applete. - Nech
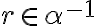 a nech
a nech
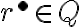 má vlastnosť
má vlastnosť
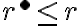 . Potom aj racionálne číslo
. Potom aj racionálne číslo
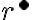 patrí do rezu:
patrí do rezu:
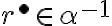 .
. - Rez
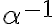 nemá najväčší prvok. Dokážeme nepriamo:
nemá najväčší prvok. Dokážeme nepriamo: - Nastavte obrázok ...
- dôkaz je podobný
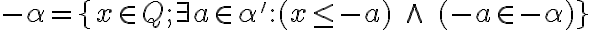 nie je nutná podmienka
nie je nutná podmienka 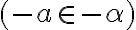 . Dá sa dokázať, že prvok
. Dá sa dokázať, že prvok
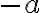 je prvkom rezu
je prvkom rezu
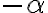 .
.
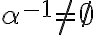 .
.
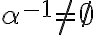 obsahuje aspoň jedno kladné racionálne čéslo, tak obsahuje aj všetky záporné racionálne čísla (prečo?).
obsahuje aspoň jedno kladné racionálne čéslo, tak obsahuje aj všetky záporné racionálne čísla (prečo?).
Teleso R,+,x
Mocnina s reálnym exponentom
Preskúmajte resp. riešte.
Mocniny
-
Mocnina
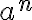 s prirodzeným exponentom
s prirodzeným exponentom 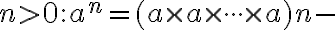 krát
krát - Mocnina
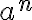 s exponentom
s exponentom 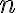 , ktorým je záporné celé číslo:
, ktorým je záporné celé číslo: 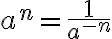
- Mocniny s racionálnym exponentom. Nech reálne číslo
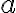 je kladné a nech
je kladné a nech 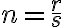 je racionálny exponent , kde
je racionálny exponent , kde  je celé číslo a
je celé číslo a 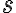 je kladné celé číslo. Potom je možné robiť úpravy typu
je kladné celé číslo. Potom je možné robiť úpravy typu
-
Predtým ako vo všeobecnosti zadefinujeme mocninu s racionálnym exponentom, tak si pripomenieme riešenie rovníc typu
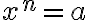 .
.
![a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r](https://lms.umb.sk/filter/tex/pix.php/3e7b97dda331b0af77ba047a99702a02.png)
Nezáporná pravá strana
Ak reálne číslo 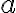 je kladné a
je kladné a  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 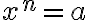 má
má
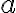 je kladné a
je kladné a  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 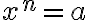 má
má
-
Reálne riešenie
![x= \sqrt[n]{a} x= \sqrt[n]{a}](https://lms.umb.sk/filter/tex/pix.php/7591b7037f09a6a1676ba7bed913935e.png) (zápis aj v tvare
(zápis aj v tvare ![a^{ \frac{1}{n} }: 8^{\frac{1}{3}}= \sqrt[3]{8} =2 a^{ \frac{1}{n} }: 8^{\frac{1}{3}}= \sqrt[3]{8} =2](https://lms.umb.sk/filter/tex/pix.php/18bc46a70060e42cb744e59bf86feb2b.png) ). Skutočnosť, že
). Skutočnosť, že 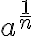 je riešením rovnice vyplýva aj z toho, že po dosadení do ľavej strany rovnice dostaneme
je riešením rovnice vyplýva aj z toho, že po dosadení do ľavej strany rovnice dostaneme - v prípade, že
 je párne, potom riešením rovnice
je párne, potom riešením rovnice 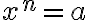 sú aj dva reálne korene, ktoré sú navzájom opačné: t. j.
sú aj dva reálne korene, ktoré sú navzájom opačné: t. j. -
ak je
 nepárne, potom rovnica
nepárne, potom rovnica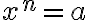 má aj kladný reálny koreň
má aj kladný reálny koreň
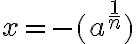 .
.
- Vo všeobecnosti: Ak reálne číslo
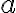 je kladné, tak v obore komplexných čísel má rovnica
je kladné, tak v obore komplexných čísel má rovnica 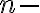 tého stupňa práve
tého stupňa práve  koreňov.
koreňov.
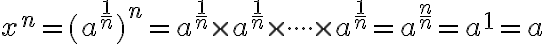
![x_1=a^{ \frac{1}{n} }= \sqrt[n]{a} >0 x_1=a^{ \frac{1}{n} }= \sqrt[n]{a} >0](https://lms.umb.sk/filter/tex/pix.php/513ff965cf0bf4314986fddb07b33cad.png)
![x_2=-(a^{ \frac{1}{n} })= -\sqrt[n]{a} x_2=-(a^{ \frac{1}{n} })= -\sqrt[n]{a}](https://lms.umb.sk/filter/tex/pix.php/9085fe8a62506f64a31b37646e6a6f01.png)
Záporná pravá strana
Nech reálne číslo 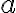 je záporné a nech
je záporné a nech  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 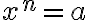
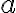 je záporné a nech
je záporné a nech  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 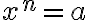
-
V prípade, že
 je párne celé číslo, potom rovnica
je párne celé číslo, potom rovnica 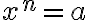
- nemá riešenie v obore reálnych čísel
- v obore komplexných má
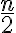 komplexne združených koreňov (Riešte
komplexne združených koreňov (Riešte 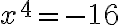 ).
).
-
Ak je
 nepárne, potom rovnica
nepárne, potom rovnica 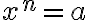 má jeden reálny koreň
má jeden reálny koreň 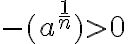 a
a 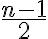 komplexne združených koreňov (Riešte
komplexne združených koreňov (Riešte 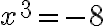 ).
).
Z uvedeného vyplýva, že mocnina s racionálnym exponentom existuje aj pre záporný základ ale v tom prípade musí byť exponent „nepárny“ (prípady 1. a 2.).
Racionálny exponent
Napíšte definíciu mocniny s racionálnym exponentom pre nezáporný aj záporný základ. Použite napríklad text Mocniny
Komplexné čísla - história
Historický rámec zavedenia pojmu komplexného čísla
- Motivačným zdrojom pre zavedenie oboru komplexných čísel nebol problém riešenia kvadratickej rovnice so záporným diskriminantom.
- Podnetom bol iný problém: algebraické riešenie kubických rovníc.
Kubická rovnica
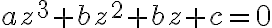 sa po substitúcii
sa po substitúcii
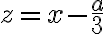 redukuje na tvar
redukuje na tvar
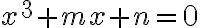 (14.st., Florencia).
(14.st., Florencia).
Potom stačí uvažovať o troch typoch kubických rovníc: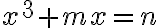 ,
,
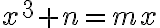 a
a
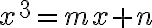 , kde
, kde
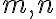 sú kladné koeficienty.
sú kladné koeficienty.
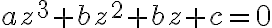 sa po substitúcii
sa po substitúcii
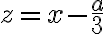 redukuje na tvar
redukuje na tvar
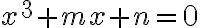 (14.st., Florencia).
(14.st., Florencia).
Potom stačí uvažovať o troch typoch kubických rovníc:
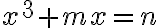 ,
,
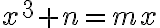 a
a
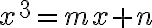 , kde
, kde
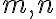 sú kladné koeficienty.
sú kladné koeficienty.
Kubickú rovnicu
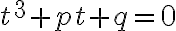 môžeme riešiť
môžeme riešiť
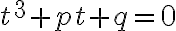 môžeme riešiť
môžeme riešiť
- substitúciou
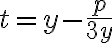 , ktorú použil Thomas Harriot (1560-1621)
, ktorú použil Thomas Harriot (1560-1621) - dostaneme rovnicu šiesteho stupňa, ktorá po úprave vedie k riešeniu
- alebo originál Cardanovou metódou, pozri Wikipédiu. Genialita Cardanovho riešenia spočíta v zavedení
Rozšírenie oboru R
V opačnom prípade, ak by existovalo reálne číslo
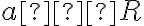 , ktoré je koreňom hľadanej rovnice, tak musí byť splnená rovnosť
, ktoré je koreňom hľadanej rovnice, tak musí byť splnená rovnosť
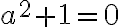 . Súčet na ľavej strane rovnosti je súčtom dvoch reálnych čísel:
. Súčet na ľavej strane rovnosti je súčtom dvoch reálnych čísel:
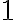 . Teda platí
. Teda platí
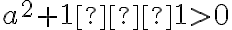 . To je spor s predpokladom, že existuje reálne číslo
. To je spor s predpokladom, že existuje reálne číslo
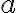 , ktoré je riešením rovnice
, ktoré je riešením rovnice
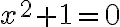 .
.
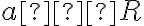 , ktoré je koreňom hľadanej rovnice, tak musí byť splnená rovnosť
, ktoré je koreňom hľadanej rovnice, tak musí byť splnená rovnosť
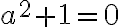 . Súčet na ľavej strane rovnosti je súčtom dvoch reálnych čísel:
. Súčet na ľavej strane rovnosti je súčtom dvoch reálnych čísel:
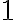 . Teda platí
. Teda platí
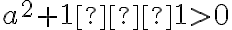 . To je spor s predpokladom, že existuje reálne číslo
. To je spor s predpokladom, že existuje reálne číslo
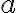 , ktoré je riešením rovnice
, ktoré je riešením rovnice
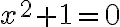 .
.
Obor komplexných čísel
Nech platí
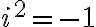 , potom môžeme zaviesť mocninu súčinu
, potom môžeme zaviesť mocninu súčinu 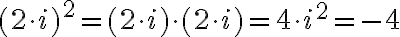 . Vo
všeobecnosti pre ľubovoľné reálne číslo
. Vo
všeobecnosti pre ľubovoľné reálne číslo
 definujeme
definujeme 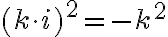 . Čísla
. Čísla
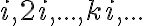 nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
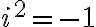 , potom môžeme zaviesť mocninu súčinu
, potom môžeme zaviesť mocninu súčinu 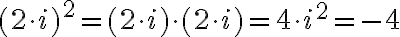 . Vo
všeobecnosti pre ľubovoľné reálne číslo
. Vo
všeobecnosti pre ľubovoľné reálne číslo
 definujeme
definujeme 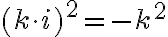 . Čísla
. Čísla
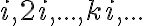 nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
Definícia
Nech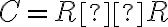 je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
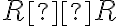 nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
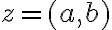 .
.
Nech
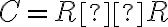 je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
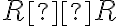 nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
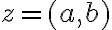 .
.
Poznámky.
Algebraický tvar
Každé komplexné číslo
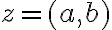 možno zapísať v tvare
možno zapísať v tvare
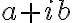 , kde
, kde
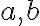 sú reálne čísla a
sú reálne čísla a
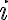 je imaginárna jednotka, pre ktorú platí
je imaginárna jednotka, pre ktorú platí
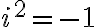 .
.
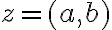 možno zapísať v tvare
možno zapísať v tvare
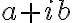 , kde
, kde
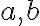 sú reálne čísla a
sú reálne čísla a
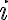 je imaginárna jednotka, pre ktorú platí
je imaginárna jednotka, pre ktorú platí
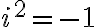 .
.
Operácie súčet a súčin zavedieme ako súčet a súčin algebraických dvojčlenov:
• pre súčet komplexných čísel bude platiť: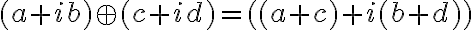
• pre súčin komplexných čísel bude platiť: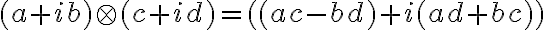
Z definície súčinu vyplýva zaujímavá vlastnosť. Ak jedno z komplexných čísel bude reálne (napr.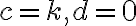 ), tak
), tak
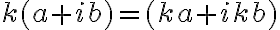 .
.
• pre súčet komplexných čísel bude platiť:
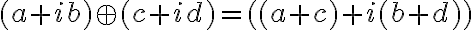
• pre súčin komplexných čísel bude platiť:
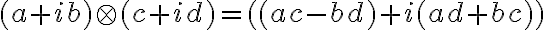
Z definície súčinu vyplýva zaujímavá vlastnosť. Ak jedno z komplexných čísel bude reálne (napr.
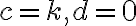 ), tak
), tak
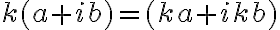 .
.
Geometrická interpretácia
Geometrická interpretácia - Gaussova komplexná rovina
Existuje bijektívne zobrazenie
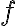 („prosté“ a „na“) množiny všetkých komplexných čísel
(„prosté“ a „na“) množiny všetkých komplexných čísel
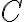 na euklidovskú rovinu
na euklidovskú rovinu
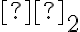 :
:
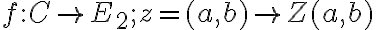 ,
,
kde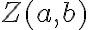 je bod
je bod
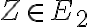 so súradnicami
so súradnicami
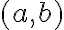 .
.
Ak v rovine zvolíme pravouhlý súradnicový systém, tak obrazom každého komplexného čísla bude práve jeden bod roviny. Obrazom komplexného čísla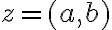 resp.
resp.
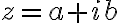 je bod
je bod
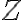 so súradnicami
so súradnicami
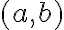 . Pozri obrázok.
. Pozri obrázok.
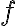 („prosté“ a „na“) množiny všetkých komplexných čísel
(„prosté“ a „na“) množiny všetkých komplexných čísel
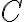 na euklidovskú rovinu
na euklidovskú rovinu
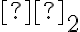 :
:
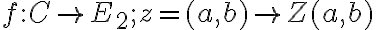 ,
,
kde
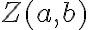 je bod
je bod
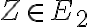 so súradnicami
so súradnicami
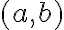 .
.
Ak v rovine zvolíme pravouhlý súradnicový systém, tak obrazom každého komplexného čísla bude práve jeden bod roviny. Obrazom komplexného čísla
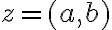 resp.
resp.
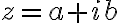 je bod
je bod
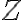 so súradnicami
so súradnicami
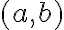 . Pozri obrázok.
. Pozri obrázok.
Zrejme platia rovnosti:
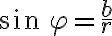 ,
,
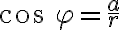 , kde
, kde
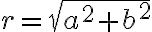 a
a
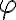 je orientovaný uhol
je orientovaný uhol
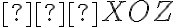 .
.
Číslo predstavuje veľkosť vektora
predstavuje veľkosť vektora
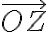 a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
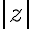 : platí
: platí
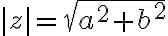 .
.
Z rovností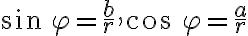 môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
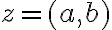 . Dostaneme
. Dostaneme
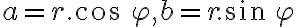 . Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
. Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
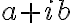 . Dostaneme nový zápis resp. nový tvar komplexného čísla
. Dostaneme nový zápis resp. nový tvar komplexného čísla
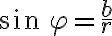 ,
,
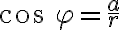 , kde
, kde
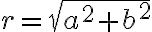 a
a
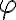 je orientovaný uhol
je orientovaný uhol
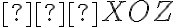 .
.
Číslo
 predstavuje veľkosť vektora
predstavuje veľkosť vektora
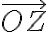 a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
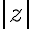 : platí
: platí
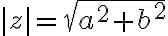 .
.
Z rovností
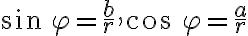 môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
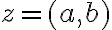 . Dostaneme
. Dostaneme
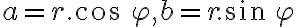 . Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
. Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
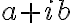 . Dostaneme nový zápis resp. nový tvar komplexného čísla
. Dostaneme nový zápis resp. nový tvar komplexného čísla
Nájdite goniometrický zápis komplexného čísla
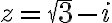 .
.
Riešenie
Najskôr si vypočítame absolútnu hodnotu hľadaného komplexného čísla. Vypočítame, že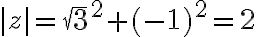 .
.
Potom určíme veľkosť uhla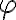 , pre ktorý platí
, pre ktorý platí
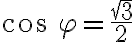 a
a
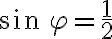 . Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
. Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
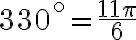 .
.
Goniometrický tvar komplexného čísla je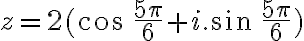 .
.
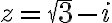 .
.
Riešenie
Najskôr si vypočítame absolútnu hodnotu hľadaného komplexného čísla. Vypočítame, že
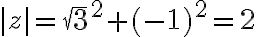 .
.
Potom určíme veľkosť uhla
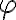 , pre ktorý platí
, pre ktorý platí
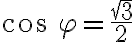 a
a
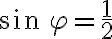 . Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
. Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
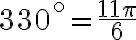 .
.
Goniometrický tvar komplexného čísla je
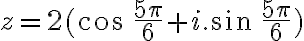 .
.
Vlastnosti operácií
Pre súčet a súčin komplexných čísel platí vlastnosť komutatívnosti a asociatívnosti, pričom súčin je distributívny k sčítaniu.
Niektoré algebraické vlastnosti komplexných čísel:
Ukážeme napríklad, že platí komutatívnosť sčítania.
- neutrálny (nulový) prvok pre sčítanie je komplexné číslo
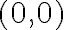
- neutrálny (jednotkový) prvok pre násobenie je komplexné číslo
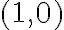
- k ľubovoľnému komplexnému číslu
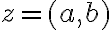 existuje inverzný prvok vzhľadom na sčítanie
existuje inverzný prvok vzhľadom na sčítanie - k ľubovoľnému nenulovému komplexnému číslu
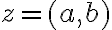 existuje inverzný prvok vzhľadom na súčin
Prvé tri vlastnosti vyplývajú priamo z definície operácií sčítania a násobenia v obore komplexných čísel.
existuje inverzný prvok vzhľadom na súčin
Prvé tri vlastnosti vyplývajú priamo z definície operácií sčítania a násobenia v obore komplexných čísel.
- Dôkaz komutatívnosti:
- Ľavú stranu skúmanej rovnosti upravíme aplikovaním definície súčtu komplexných čísel, ktoré sme vyjadrili v algebrickom tvare
- Pravú stranu rovnosti tiež upravme aplikovaním definície súčtu komplexných čísel.
- V prvom aj v druhom prípade sme dostali rovnaký výsledok. To znamená, že platí komutatívny zákon pre sčítanie komplexných čísel.
- Dokážte štvrtú vlastnosť konštruktívnym spôsobom:
- predpokladajte, že existuje inverzný prvok
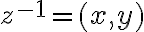 ku komplexnému číslu
ku komplexnému číslu
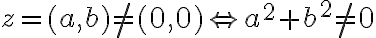
- potom musí platiť rovnosť
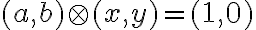 , ale táto rovnosť predstavuje rovnicu o dvoch neznámych
, ale táto rovnosť predstavuje rovnicu o dvoch neznámych
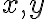
- upravme ju na tvar
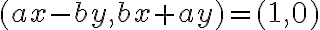 .
. - porovnanie usporiadaných dvojíc vedie na sústavu dvoch rovníc o dvoch neznámych
-
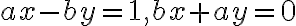 ,
, - ktorej riešením sú reálne čísla
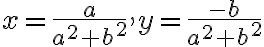 . Pozrite si stránku Matrix calculator.
. Pozrite si stránku Matrix calculator.
Vlastnosti absolútnej hodnoty
Moivreova veta
Francúzsky matematik Abraham de Moivre sformuloval vetu, podľa ktorej môžeme jednoducho umocňovať komplexné čísla vyjadrené v goniometrickom tvare.
Moivrovu vetu pre mocninu dokážeme napríklad pomocou matematickej indukcie, pričom využijeme súčtové vzorce pre sínus a kosínus. Z Moivreovej vety vyplýva aj jej odvodený tvar pre súčin dvoch komplexných čísel.
Poznámky.
- Dôležité je uvedomiť si, že komplexnými číslami končí rozširovanie číselného oboru.
- V roku 1799 Gauss dokázal, že každá algebraická rovnica, ktorej koeficienty sú komplexné čísla, má v obore komplexných čísel riešenie.
- To znamená, že obor komplexných čísel už nie je potrebné ďalej rozširovať.
Príklady
- Ak existuje komplexné číslo
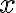 , tak ho možno napísať v algebraickom tvare ako
, tak ho možno napísať v algebraickom tvare ako
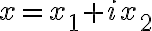 .
. - Potom naša rovnica bude mať tvar
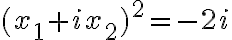 čiže
čiže
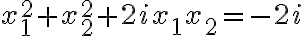 .
. - Z definície rovnosti komplexných čísel vyplýva, že
- Ľavú stranu prvej rovnice rozložíme na súčin podľa vzorca pre rozdiel štvorcov:
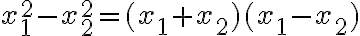 . Tým sa zbavíme druhých mocnín. Vieme, že súčin dvoch čísel sa rovná nule, ak aspoň jeden z činiteľov je rovný nule. Teda buď
. Tým sa zbavíme druhých mocnín. Vieme, že súčin dvoch čísel sa rovná nule, ak aspoň jeden z činiteľov je rovný nule. Teda buď
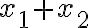 , alebo
, alebo
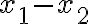
- Ak do druhej rovnice dosadíme
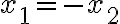 dostaneme
dostaneme
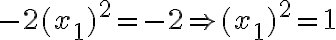 . Táto rovnica má dva reálne korene
. Táto rovnica má dva reálne korene
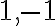 .
. - Ak predpokladáme, že
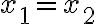 , tak dosadením do druhej rovnice dostaneme
, tak dosadením do druhej rovnice dostaneme
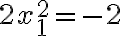 . Táto rovnica však nemá reálne korene!
. Táto rovnica však nemá reálne korene!
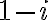 a číslo
a číslo
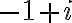 , ktoré sú koreňmi rovnice
, ktoré sú koreňmi rovnice
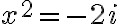 .
.
Vyriešte tento príklad pomocou goniometrického tvaru komplexného čísla.
Pri riešení rovnice vlastne hľadáme druhú odmocninu komplexného čísla.
Položte si otázku, či vždy existuje druhá odmocnina z komplexného čísla. Pokúste sa dokázať, že áno.
Jarník, Jiří: Komplexní čísla a funkce. Praha: Mladá fronta, 1967. Dostupné na Czech Digital Mathematics Library Tu
Položte si otázku, či vždy existuje druhá odmocnina z komplexného čísla. Pokúste sa dokázať, že áno.
Jarník, Jiří: Komplexní čísla a funkce. Praha: Mladá fronta, 1967. Dostupné na Czech Digital Mathematics Library Tu
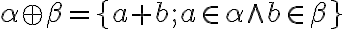
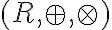
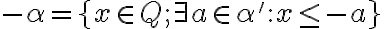
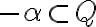
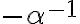
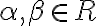
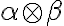
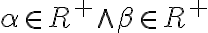
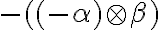
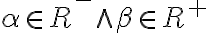
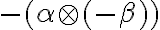
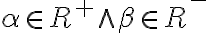
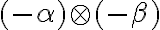
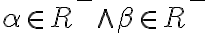
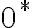
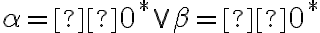
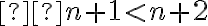
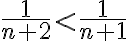
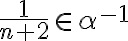
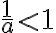
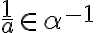
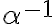
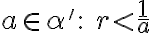
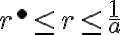
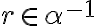
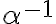
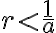
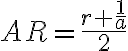
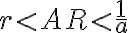
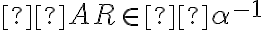
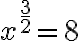
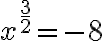
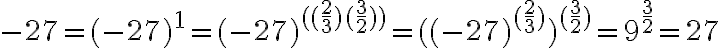
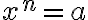
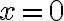
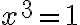
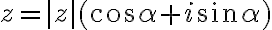
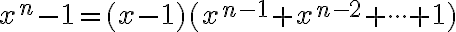
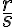
![x^{ \frac{3}{2} }=-27 \Leftrightarrow (-27)^{ \frac{2}{3} }= \sqrt[3]{(-27)^2} = \sqrt[3]{27^2} = \sqrt[3]{9^3} =9>0 x^{ \frac{3}{2} }=-27 \Leftrightarrow (-27)^{ \frac{2}{3} }= \sqrt[3]{(-27)^2} = \sqrt[3]{27^2} = \sqrt[3]{9^3} =9>0](https://lms.umb.sk/filter/tex/pix.php/0930ff8a640ddf217b21ff2adb00634b.png)
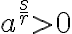
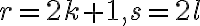
![x^{ \frac{3}{1} }=-27 \Leftrightarrow (-27)^{ \frac{1}{3} }= \sqrt[3]{(-27)^1} = -3 x^{ \frac{3}{1} }=-27 \Leftrightarrow (-27)^{ \frac{1}{3} }= \sqrt[3]{(-27)^1} = -3](https://lms.umb.sk/filter/tex/pix.php/54704b81a2a34b688859939b74705ee2.png)