Celé čísla a racionálne čísla
celé čísla
Obor celých čísel
Definícia.
Nech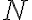 je množina všetkých prirodzených čísel. Definujme binárnu reláciu
je množina všetkých prirodzených čísel. Definujme binárnu reláciu
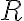 na množine
na množine
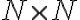 takto:
takto:
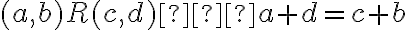 .
.
Nech
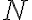 je množina všetkých prirodzených čísel. Definujme binárnu reláciu
je množina všetkých prirodzených čísel. Definujme binárnu reláciu
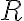 na množine
na množine
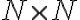 takto:
takto:
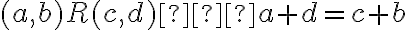 .
.
Dve usporiadané dvojice prirodzených čísel
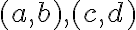 sú v relácii, ak platí rovnosť
sú v relácii, ak platí rovnosť
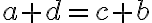
(súčet prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčtu prvého člena druhej dvojice s druhým členom prvej dvojice).
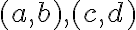 sú v relácii, ak platí rovnosť
sú v relácii, ak platí rovnosť
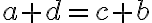
(súčet prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčtu prvého člena druhej dvojice s druhým členom prvej dvojice).
-
Nech
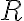 je binárna relácia s požadovanou vlastnosťou a nech
je binárna relácia s požadovanou vlastnosťou a nech
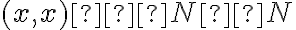 je ľubovoľná dvojica prirodzených čísel. Potom zrejme platí
je ľubovoľná dvojica prirodzených čísel. Potom zrejme platí
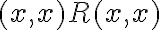 , lebo platí
, lebo platí
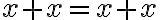 . Odkiaľ dostaneme, že relácia
. Odkiaľ dostaneme, že relácia
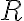 je reflexívna.
je reflexívna. - Nech ľubovoľné dve usporiadané dvojice sú v relácii
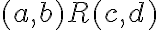 .
. - Rovnosť prirodzených čísel je symetrická, preto tiež platí:
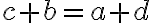 .
. - To je ekvivalentné so vzťahom
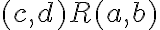 , preto platí: relácia
, preto platí: relácia
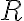 je symetrická.
je symetrická. - Nech platí
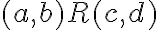 a zároveň
a zároveň
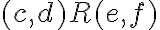 .
. - Z definície relácie
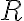 vyplýva, že musí platiť
vyplýva, že musí platiť
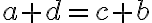 a zároveň
a zároveň
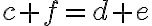 . Pripočítajme k prvej rovnosti číslo
. Pripočítajme k prvej rovnosti číslo
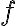 a k druhej rovnosti číslo
a k druhej rovnosti číslo
 .
. - Dostaneme rovnosti
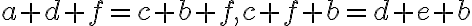 . Zrejme platí
. Zrejme platí
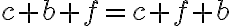 (komutatívnosť sčítania).
(komutatívnosť sčítania). - Ak využijeme, že rovnosť prirodzených čísel je tranzitívna, tak dostaneme
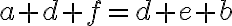 .
. - Teraz stačí aplikovať komutatívnosť a vetu o krátení a dostaneme
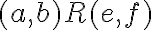 . To znamená, že relácia
. To znamená, že relácia
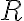 je tranzitívna.
je tranzitívna.
