Množinová aritmetika
Peano
Množinová aritmetika
Ústredným pojmom pri množinovom prístupe v aritmetike prirodzených čísel je pojem ekvivalentnosti dvoch množín.
Pri jeho zavedení sa budeme opierať o bijektívne zobrazenie medzi dvoma množinami. Pri konečných množinách si takéto zobrazenie môžeme predstaviť tak, že prvky dvoch množín navzájom pospájame podľa pravidla „jeden len s jedným“. Takéto pravidlo používajú
aj deti na prvom stupni ZŠ.
Definícia.
Hovoríme, že množina je ekvivalentná s množinou
je ekvivalentná s množinou  , ak existuje prosté zobrazenie
, ak existuje prosté zobrazenie 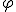 množiny
množiny  na množinu
na množinu  .
.
Skutočnosť, že množina je ekvivalentná s množinou
je ekvivalentná s množinou  budeme zapisovať symbolom
budeme zapisovať symbolom 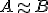 . Zobrazenie
. Zobrazenie 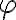 je zrejme bijekcia.
je zrejme bijekcia.
Hovoríme, že množina
 je ekvivalentná s množinou
je ekvivalentná s množinou  , ak existuje prosté zobrazenie
, ak existuje prosté zobrazenie 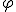 množiny
množiny  na množinu
na množinu  .
.
Skutočnosť, že množina
 je ekvivalentná s množinou
je ekvivalentná s množinou  budeme zapisovať symbolom
budeme zapisovať symbolom 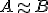 . Zobrazenie
. Zobrazenie 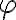 je zrejme bijekcia.
je zrejme bijekcia.
Príklad.
Nech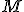 je nekonečná množina a
je nekonečná množina a 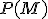 jej potenčná množina. Definujme binárnu reláciu
jej potenčná množina. Definujme binárnu reláciu 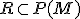 tak, aby
tak, aby
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/782f09dd57dd917afb64567badbf371d.png) .
.
Nech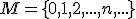 je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
Nech
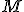 je nekonečná množina a
je nekonečná množina a 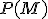 jej potenčná množina. Definujme binárnu reláciu
jej potenčná množina. Definujme binárnu reláciu 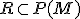 tak, aby
tak, aby
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/782f09dd57dd917afb64567badbf371d.png) .
.
Nech
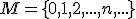 je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
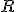
![\small [ \lbrace{0}\rbrace, \lbrace{0}\rbrace], [ \lbrace{0}\rbrace, \lbrace{1}\rbrace], ...,[ \lbrace{0}\rbrace, \lbrace{n}\rbrace], ... \small [ \lbrace{0}\rbrace, \lbrace{0}\rbrace], [ \lbrace{0}\rbrace, \lbrace{1}\rbrace], ...,[ \lbrace{0}\rbrace, \lbrace{n}\rbrace], ...](https://lms.umb.sk/filter/tex/pix.php/22286cf5621be8d62cbd77f375365f45.png)
![\small [ \lbrace{0,1}\rbrace, \lbrace{0,2}\rbrace], ...,[\lbrace{0,1}\rbrace,\lbrace{0,n}\rbrace], ...,[ \lbrace{1,2}\rbrace,,\lbrace{1,n}\rbrace], ... \small [ \lbrace{0,1}\rbrace, \lbrace{0,2}\rbrace], ...,[\lbrace{0,1}\rbrace,\lbrace{0,n}\rbrace], ...,[ \lbrace{1,2}\rbrace,,\lbrace{1,n}\rbrace], ...](https://lms.umb.sk/filter/tex/pix.php/b7976e0c2c7122ebcaf715e584400a50.png)
![\small [ \lbrace{0,1,2}\rbrace, \lbrace{0,1,3}\rbrace], ..., [ \lbrace{1,2,3}\rbrace,\lbrace{1,2,,n}\rbrace], ... \small [ \lbrace{0,1,2}\rbrace, \lbrace{0,1,3}\rbrace], ..., [ \lbrace{1,2,3}\rbrace,\lbrace{1,2,,n}\rbrace], ...](https://lms.umb.sk/filter/tex/pix.php/44c53c81d9e2ebbf1dcf847abc5fe996.png)
