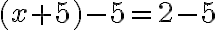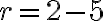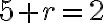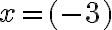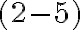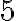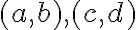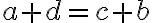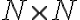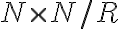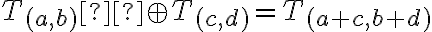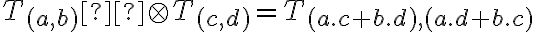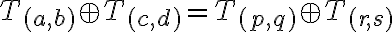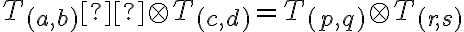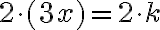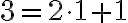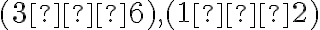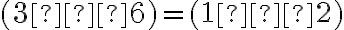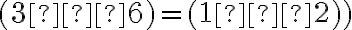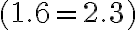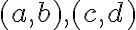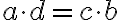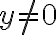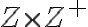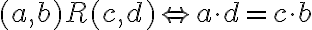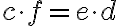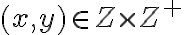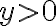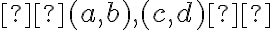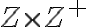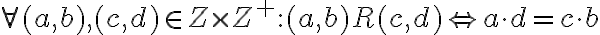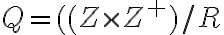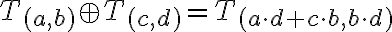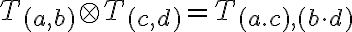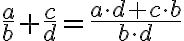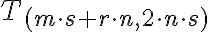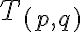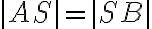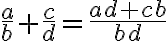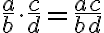Celé čísla a racionálne čísla
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Celé čísla a racionálne čísla |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:41 |
Opis
celé čísla
Celé čísla - úvod
Naše vedomosti z elementárnej matematiky nám napovedajú, že riešenie existuje v inom číselnom obore, v obore celých čísel. Jednoducho, ak budeme aplikovať jednu z ekvivalentných úprav „odčítanie“ čísla 5 k obidvom stranám rovnice, tak dostaneme
Po úprave na ľavej strane rovnice dostaneme
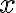 , ale na pravej strane rovnice to nie je prirodzené číslo. Výsledkom je "číslo
, ale na pravej strane rovnice to nie je prirodzené číslo. Výsledkom je "číslo
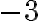 ". Toto riešenie skrýva v sebe základnú myšlienku pre zavedenie celých čísel – metódu odčítania.
". Toto riešenie skrýva v sebe základnú myšlienku pre zavedenie celých čísel – metódu odčítania.
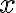 , ale na pravej strane rovnice to nie je prirodzené číslo. Výsledkom je "číslo
, ale na pravej strane rovnice to nie je prirodzené číslo. Výsledkom je "číslo
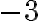 ". Toto riešenie skrýva v sebe základnú myšlienku pre zavedenie celých čísel – metódu odčítania.
". Toto riešenie skrýva v sebe základnú myšlienku pre zavedenie celých čísel – metódu odčítania.
Nech
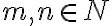 sú prirodzené čísla. Ak existuje jediné prirodzené číslo
sú prirodzené čísla. Ak existuje jediné prirodzené číslo
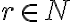 , pre ktoré je splnená rovnosť
, pre ktoré je splnená rovnosť
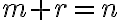 , tak toto číslo nazveme rozdielom čísel
, tak toto číslo nazveme rozdielom čísel
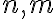 v tomto poradí a budeme ho označovať symbolom
v tomto poradí a budeme ho označovať symbolom
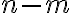 .
.
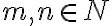 sú prirodzené čísla. Ak existuje jediné prirodzené číslo
sú prirodzené čísla. Ak existuje jediné prirodzené číslo
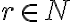 , pre ktoré je splnená rovnosť
, pre ktoré je splnená rovnosť
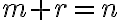 , tak toto číslo nazveme rozdielom čísel
, tak toto číslo nazveme rozdielom čísel
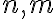 v tomto poradí a budeme ho označovať symbolom
v tomto poradí a budeme ho označovať symbolom
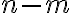 .
.
Opačné číslo
Na vyjadrenie hodnoty menšej ako nula (teplota pod 0^° C a pod.) používame opačné čísla k prirodzeným číslam.
• Opačné číslo k prirodzenému číslu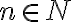 ak označme symbolom
ak označme symbolom
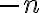 , tak bude platiť
, tak bude platiť 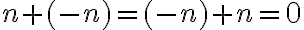 .
.
• Číslo opačné k prirodzenému číslu budeme nazývať záporné číslo.
• Opačné číslo k prirodzenému číslu
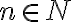 ak označme symbolom
ak označme symbolom
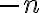 , tak bude platiť
, tak bude platiť 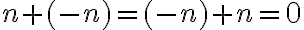 .
.
• Číslo opačné k prirodzenému číslu budeme nazývať záporné číslo.
Napríklad pri interpretácii pojmu záporného čísla
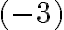 s výhodou používame termín „pasíva“. Na druhej strane prirodzené číslo
s výhodou používame termín „pasíva“. Na druhej strane prirodzené číslo
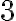 interpretujme ako „aktíva“. Žiaci potom budú prirodzene chápať, že platí aj rovnosť
interpretujme ako „aktíva“. Žiaci potom budú prirodzene chápať, že platí aj rovnosť
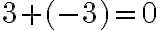 alebo rovnosť
alebo rovnosť
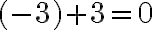 .
.
Túto rovnosť potom využijú pri riešení rovnice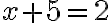 . Po jednoduchej úprave (asociatívnosť sčítania prirodzených čísel) dostanú rovnicu
. Po jednoduchej úprave (asociatívnosť sčítania prirodzených čísel) dostanú rovnicu
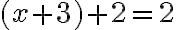 .
.
Žiaci už vedia odčítať to isté prirodzené číslo od obidvoch strán rovnice. Ak odčítajú číslo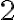 , tak po odčítaní dostanú „jednoduchšiu“ rovnicu
, tak po odčítaní dostanú „jednoduchšiu“ rovnicu
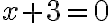 .
.
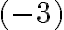 s výhodou používame termín „pasíva“. Na druhej strane prirodzené číslo
s výhodou používame termín „pasíva“. Na druhej strane prirodzené číslo
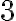 interpretujme ako „aktíva“. Žiaci potom budú prirodzene chápať, že platí aj rovnosť
interpretujme ako „aktíva“. Žiaci potom budú prirodzene chápať, že platí aj rovnosť
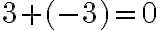 alebo rovnosť
alebo rovnosť
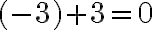 .
.
Túto rovnosť potom využijú pri riešení rovnice
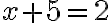 . Po jednoduchej úprave (asociatívnosť sčítania prirodzených čísel) dostanú rovnicu
. Po jednoduchej úprave (asociatívnosť sčítania prirodzených čísel) dostanú rovnicu
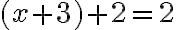 .
.
Žiaci už vedia odčítať to isté prirodzené číslo od obidvoch strán rovnice. Ak odčítajú číslo
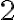 , tak po odčítaní dostanú „jednoduchšiu“ rovnicu
, tak po odčítaní dostanú „jednoduchšiu“ rovnicu
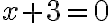 .
.
Záporné čísla
Záporné čísla
sa objavili po prvýkrát v čínskej matematike. V knihe „Deväť kapitol matematického umenia“ (202 pred n.l.) sú použité červené „úsečky“ pre kladné čísla a čierne pre záporné čísla.
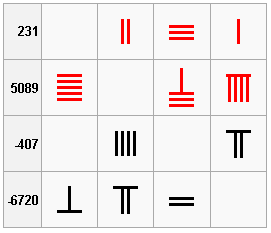
Tento systém je opak súčasného zapisovania kladných a záporných čísel v oblasti bankovníctva, účtovníctva a obchode.
- V 7. storočí nášho letopočtu v Indii, boli záporné čísla použité na vyjadrenie dlhu. Indický matematik Brahmagupta, uvádza pravidlá pre operácie sčítania a násobenia so zápornými číslami. Používal termíny "dlh“ a „úver“.
- Európski matematici sa bránili konceptu záporných číslach až do 17. storočia, hoci Fibonacci používal pri riešení finančných problémov záporné čísla (Libier Abaci, 1202).
- Gottfried Wilhelm Leibniz bol prvý matematik, ktorý systematicky využíval záporné čísla.
Poznámky.
- Matematici v rôznych obdobiach považovali záporné čísla za absurdné (Diofantos), klamné (Descart) a fiktívne (Bombelli).
- Pozrite si modely záporných čísel, ktoré sa používajú vo vyučovaní matematiky. Tu
Celé čísla ako rozdiely
Celé čísla môžeme v širšom význame chápať ako všetky možné rozdiely dvoch prirodzených čísel. Problém je však v tom, že niektoré rozdiely neexistujú v obore prirodzených čísel.
Napríklad ako sme už poukázali rozdiel
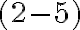 , ktorý by mal byť riešením našej rovnice neexistuje v množine prirodzených čísel. Na druhej strane, zrejme aj rozdiel
, ktorý by mal byť riešením našej rovnice neexistuje v množine prirodzených čísel. Na druhej strane, zrejme aj rozdiel
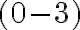 je riešením našej rovnice.
je riešením našej rovnice.
Všimnime si jednu podstatnú skutočnosť. Ak rozdiel prirodzených čísel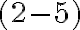 a zároveň aj rozdiel
a zároveň aj rozdiel
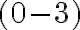 je hľadaným riešením rovnice, tak musí platiť rovnosť
je hľadaným riešením rovnice, tak musí platiť rovnosť
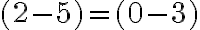 .
.
Po jednoduchej úprave (postupné pričítanie čísla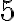 a čísla
a čísla
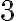 k obidvom stranám rovnosti) dostaneme rovnosť
k obidvom stranám rovnosti) dostaneme rovnosť
(2+3=0+5\).
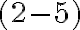 , ktorý by mal byť riešením našej rovnice neexistuje v množine prirodzených čísel. Na druhej strane, zrejme aj rozdiel
, ktorý by mal byť riešením našej rovnice neexistuje v množine prirodzených čísel. Na druhej strane, zrejme aj rozdiel
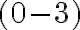 je riešením našej rovnice.
je riešením našej rovnice.
Všimnime si jednu podstatnú skutočnosť. Ak rozdiel prirodzených čísel
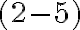 a zároveň aj rozdiel
a zároveň aj rozdiel
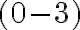 je hľadaným riešením rovnice, tak musí platiť rovnosť
je hľadaným riešením rovnice, tak musí platiť rovnosť
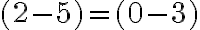 .
.
Po jednoduchej úprave (postupné pričítanie čísla
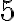 a čísla
a čísla
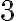 k obidvom stranám rovnosti) dostaneme rovnosť
k obidvom stranám rovnosti) dostaneme rovnosť
(2+3=0+5\).
To znamená, že dva rozdiely prirodzených čísel
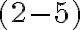 a
a
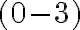 budú predstavovať to isté záporné číslo
budú predstavovať to isté záporné číslo
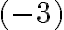 práve vtedy, ak platí rovnosť
práve vtedy, ak platí rovnosť 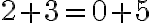 .
.
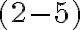 a
a
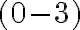 budú predstavovať to isté záporné číslo
budú predstavovať to isté záporné číslo
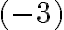 práve vtedy, ak platí rovnosť
práve vtedy, ak platí rovnosť 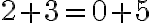 .
.
Platnosť poslednej rovnosti vieme bez problémov overiť, pretože sčitovať prirodzené čísla sme sa naučili v prvej kapitole. Z uvedeného vyplýva, že celé čísla môžeme zaviesť pomocou dvojíc prirodzených čísel.
Obor celých čísel
Definícia.
Nech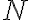 je množina všetkých prirodzených čísel. Definujme binárnu reláciu
je množina všetkých prirodzených čísel. Definujme binárnu reláciu
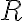 na množine
na množine
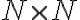 takto:
takto:
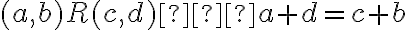 .
.
Nech
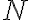 je množina všetkých prirodzených čísel. Definujme binárnu reláciu
je množina všetkých prirodzených čísel. Definujme binárnu reláciu
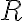 na množine
na množine
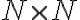 takto:
takto:
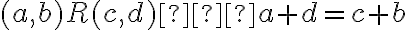 .
.
Dve usporiadané dvojice prirodzených čísel
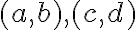 sú v relácii, ak platí rovnosť
sú v relácii, ak platí rovnosť
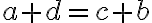
(súčet prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčtu prvého člena druhej dvojice s druhým členom prvej dvojice).
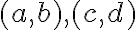 sú v relácii, ak platí rovnosť
sú v relácii, ak platí rovnosť
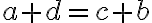
(súčet prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčtu prvého člena druhej dvojice s druhým členom prvej dvojice).
-
Nech
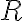 je binárna relácia s požadovanou vlastnosťou a nech
je binárna relácia s požadovanou vlastnosťou a nech
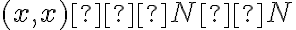 je ľubovoľná dvojica prirodzených čísel. Potom zrejme platí
je ľubovoľná dvojica prirodzených čísel. Potom zrejme platí
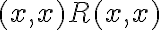 , lebo platí
, lebo platí
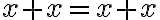 . Odkiaľ dostaneme, že relácia
. Odkiaľ dostaneme, že relácia
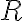 je reflexívna.
je reflexívna. - Nech ľubovoľné dve usporiadané dvojice sú v relácii
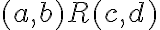 .
. - Rovnosť prirodzených čísel je symetrická, preto tiež platí:
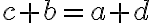 .
. - To je ekvivalentné so vzťahom
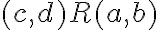 , preto platí: relácia
, preto platí: relácia
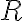 je symetrická.
je symetrická. - Nech platí
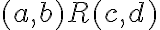 a zároveň
a zároveň
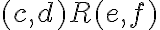 .
. - Z definície relácie
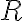 vyplýva, že musí platiť
vyplýva, že musí platiť
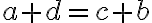 a zároveň
a zároveň
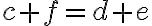 . Pripočítajme k prvej rovnosti číslo
. Pripočítajme k prvej rovnosti číslo
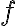 a k druhej rovnosti číslo
a k druhej rovnosti číslo
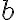 .
. - Dostaneme rovnosti
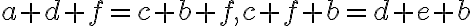 . Zrejme platí
. Zrejme platí
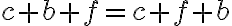 (komutatívnosť sčítania).
(komutatívnosť sčítania). - Ak využijeme, že rovnosť prirodzených čísel je tranzitívna, tak dostaneme
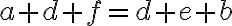 .
. - Teraz stačí aplikovať komutatívnosť a vetu o krátení a dostaneme
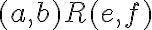 . To znamená, že relácia
. To znamená, že relácia
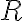 je tranzitívna.
je tranzitívna.
Rozširenie oboru N
Nech
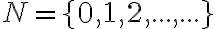 je množina všetkých prirodzených čísel. Potom rozklad
je množina všetkých prirodzených čísel. Potom rozklad
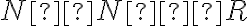 je množina, ktorej prvky-triedy sú podmnožiny karteziánskeho súčinu. Každá trieda obsahuje len prvky, ktoré sú usporiadanými dvojicami prirodzených čísel!
je množina, ktorej prvky-triedy sú podmnožiny karteziánskeho súčinu. Každá trieda obsahuje len prvky, ktoré sú usporiadanými dvojicami prirodzených čísel!
Ukážka
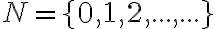 je množina všetkých prirodzených čísel. Potom rozklad
je množina všetkých prirodzených čísel. Potom rozklad
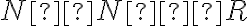 je množina, ktorej prvky-triedy sú podmnožiny karteziánskeho súčinu. Každá trieda obsahuje len prvky, ktoré sú usporiadanými dvojicami prirodzených čísel!
je množina, ktorej prvky-triedy sú podmnožiny karteziánskeho súčinu. Každá trieda obsahuje len prvky, ktoré sú usporiadanými dvojicami prirodzených čísel!
-
Označme symbolom
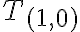 triedu, ktorá obsahuje dvojicu
triedu, ktorá obsahuje dvojicu 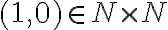 } \)\. Potom trieda
} \)\. Potom trieda
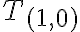 bude obsahovať aj všetky usporiadané dvojice typu
bude obsahovať aj všetky usporiadané dvojice typu
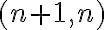 , lebo platí
, lebo platí
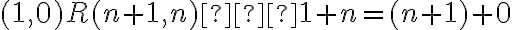 . Triedu
. Triedu
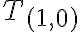 môžeme určiť vymenovaním jej prvkov:
môžeme určiť vymenovaním jej prvkov:
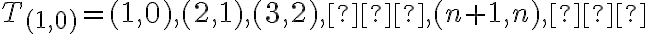 .
. -
Podobne by sme ukázali, že trieda
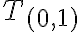 , ktorá obsahuje dvojicu
, ktorá obsahuje dvojicu
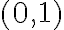 bude obsahovať aj všetky usporiadané dvojice typu
bude obsahovať aj všetky usporiadané dvojice typu
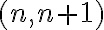 . Symbolicky
. Symbolicky
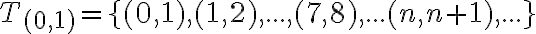 .
. -
Označenie pre triedy rozkladov
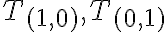 môžeme nahradiť aj inými symbolmi. V literatúre sa objavujú symboly
môžeme nahradiť aj inými symbolmi. V literatúre sa objavujú symboly
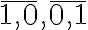 .
.
My použijeme jednoduchšie symboly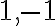 , čo sú vlastne arabské číslice pre označenie celých čísel.
, čo sú vlastne arabské číslice pre označenie celých čísel.
-
Vo všeobecnosti trieda rozkladu, do ktorej patrí usporiadaná dvojica
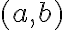 je množina, ktorá môže byť symbolicky zapísaná ako
je množina, ktorá môže byť symbolicky zapísaná ako
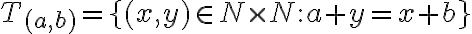 .
. -
Všimnite si, že triedy rozkladu, ktoré prináležia usporiadanej dvojici
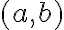 , kde
, kde
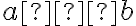 , budú reprezentované prirodzenými číslami.
, budú reprezentované prirodzenými číslami. - V prípade, že
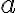 dostneme triedy rozkladu, ktoré budú reprezentované zápornými číslami.
dostneme triedy rozkladu, ktoré budú reprezentované zápornými číslami.
Množina celých čísel
Zhrňme si naše úvahy:
- Za základnú (východiskovú) množinu zvolíme množinu prirodzených čísel
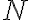 , ktorú popíšme napríklad Peanovou aritmetikou.
, ktorú popíšme napríklad Peanovou aritmetikou. - Vytvoríme množinu všetkých usporiadaných dvojíc
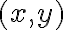 prirodzených čísel pomocou karteziánskeho súčinu
prirodzených čísel pomocou karteziánskeho súčinu
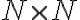 .
. - Dvojice prirodzených čísel zatriedime do skupín tak, že pre ľubovoľné dve dvojice
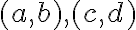 z rovnakej skupiny platí rovnosť
z rovnakej skupiny platí rovnosť
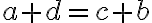 .
. - Uvedieme definíciu množiny celých čísel, ktorá vychádza z týchto úvah.
Definícia.
Nech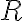 je relácia ekvivalencie na množine
je relácia ekvivalencie na množine
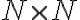 , pre ktorú platí:
, pre ktorú platí:
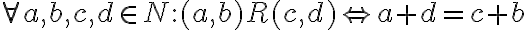
a nech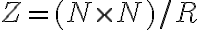 je rozklad množiny
je rozklad množiny
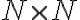 podľa relácie
podľa relácie
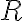 . Potom prvky množiny
. Potom prvky množiny
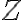 budeme nazývať celé čísla.
budeme nazývať celé čísla.
Nech
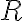 je relácia ekvivalencie na množine
je relácia ekvivalencie na množine
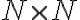 , pre ktorú platí:
, pre ktorú platí:
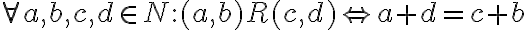
a nech
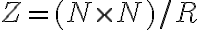 je rozklad množiny
je rozklad množiny
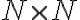 podľa relácie
podľa relácie
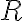 . Potom prvky množiny
. Potom prvky množiny
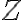 budeme nazývať celé čísla.
budeme nazývať celé čísla.
Poznámky.
Nech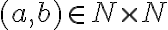 , potom v prípade:
, potom v prípade:
Nech
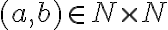 , potom v prípade:
, potom v prípade:
-
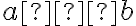 triedu rozkladu
triedu rozkladu
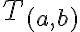 budeme označovať symbolom
budeme označovať symbolom
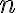 , kde
, kde
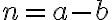 je prirodzené číslo, zrejme platí
je prirodzené číslo, zrejme platí
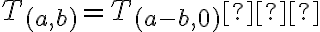
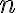 .
.
Tieto čísla budeme nazývať nezáporné celé čísla a množinu všetkých nezáporných čísel symbolom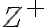 .
. -
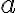 triedu rozkladu
triedu rozkladu
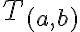 budeme označovať symbolom
budeme označovať symbolom
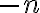 , kde
, kde
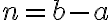 je prirodzené číslo, zrejme platí
je prirodzené číslo, zrejme platí
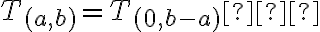
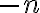 .
.
Tieto čísla budeme nazývať záporné celé čísla a množinu všetkých záporných čísel symbolom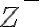 .
. - Pokúste sa definovať kladné čísla.
Súčet a súčin
Relácia ekvivalencie
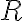 umožnila vytvorenie „nosiča“ pre celé čísla. Teraz musíme definovať súčet a súčin celých čísel.
umožnila vytvorenie „nosiča“ pre celé čísla. Teraz musíme definovať súčet a súčin celých čísel.
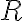 umožnila vytvorenie „nosiča“ pre celé čísla. Teraz musíme definovať súčet a súčin celých čísel.
umožnila vytvorenie „nosiča“ pre celé čísla. Teraz musíme definovať súčet a súčin celých čísel.
Nech
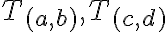 sú dve celé čísla (dve triedy rozkladu), potom súčet
sú dve celé čísla (dve triedy rozkladu), potom súčet
 a súčin
a súčin
 týchto celých čísel popisujú nasledujúce dve definície.
týchto celých čísel popisujú nasledujúce dve definície.
Interpretácia definícií
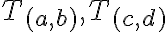 sú dve celé čísla (dve triedy rozkladu), potom súčet
sú dve celé čísla (dve triedy rozkladu), potom súčet
 a súčin
a súčin
 týchto celých čísel popisujú nasledujúce dve definície.
týchto celých čísel popisujú nasledujúce dve definície.Zvoľme si celé čísla
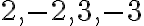 . Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
. Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
 . Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
. Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
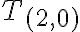 ≝ 2,
≝ 2, 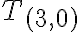 ,
≝ 3
,
≝ 3
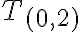 ≝ -2,
≝ -2,
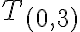 ≝ -3.
≝ -3.
Interpretujme súčet tried
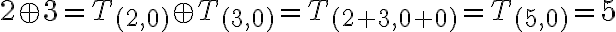
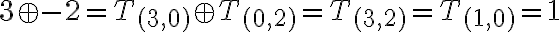
Interpretujte súčin tried
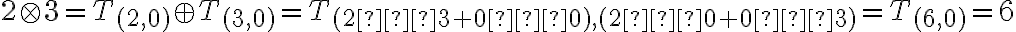
Spočítajte ďalšie možné súčty a súčiny.
Poznámky
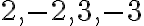 . Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
. Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
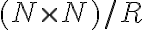 . Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
. Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
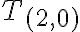 ≝ 2,
≝ 2, 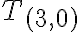 ,
≝ 3
,
≝ 3
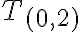 ≝ -2,
≝ -2,
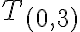 ≝ -3.
≝ -3.
Interpretujme súčet tried
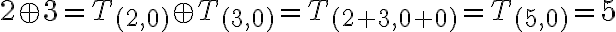
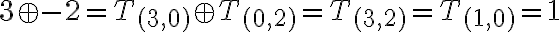
Interpretujte súčin tried
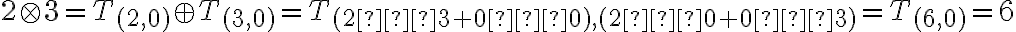
Spočítajte ďalšie možné súčty a súčiny.
-
Súčin
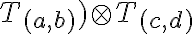 si ľahko zapamätáme pomocou súčinu dvojčlenov
si ľahko zapamätáme pomocou súčinu dvojčlenov
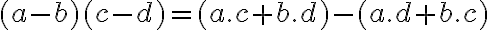 .
.
-
Vyššie definovaný súčet a súčin celých čísel je korektný. To znamená, že nie je závislý od výberu „reprezentantov“
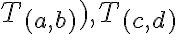 . Korektnosť definície súčtu znamená, že platí nasledujúce tvrdenie.
Ak
. Korektnosť definície súčtu znamená, že platí nasledujúce tvrdenie.
Ak -
Na základe predchádzajúcich úvah môžeme množinu celých čísel symbolicky zapísať ako množinu:
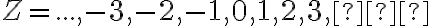
alebo
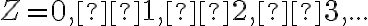 .
.
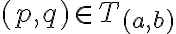 a zároveň
a zároveň
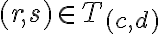 , tak:
, tak:
Vlastnosti celých čísel
Preštudujte si kapitolu Vlastnosti celých čísel v študijnom texte "Čísla a počítanie"
Absolútna hodnota
Preštudujte si kapitoly
3.2.2 Absolútna hodnota celého čísla
3.2.3 Usporiadanie na množine celých čísel
v študijnom texte "Čísla a počítanie"
Racionálne čísla - úvod
Stačí pripočítať k obidvom stranám rovnice číslo -3 a dostaneme rovnicu 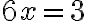 , ktorej riešením nemôže byť celé číslo.
, ktorej riešením nemôže byť celé číslo.
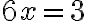 , ktorej riešením nemôže byť celé číslo.
, ktorej riešením nemôže byť celé číslo.
Na chvíľu predpokladajme, že existuje číslo, ktoré je riešením danej rovnice
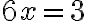 . Z predchádzajúcej kapitoly vieme, že také číslo
. Z predchádzajúcej kapitoly vieme, že také číslo
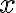 musí byť podiel
musí byť podiel
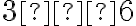 celých čísel
celých čísel
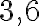 . Teda muselo by platiť:
. Teda muselo by platiť:
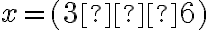 .
.
Rovnicu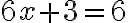 môžeme upraviť na tvar
môžeme upraviť na tvar
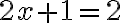 . Riešením tejto rovnice je podiel
. Riešením tejto rovnice je podiel
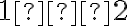 , teda
, teda
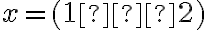 .
.
Zároveň vieme, že rovnica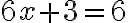 má nanajvýš jedno riešenie. Dokážte to!
má nanajvýš jedno riešenie. Dokážte to!
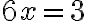 . Z predchádzajúcej kapitoly vieme, že také číslo
. Z predchádzajúcej kapitoly vieme, že také číslo
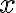 musí byť podiel
musí byť podiel
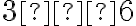 celých čísel
celých čísel
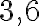 . Teda muselo by platiť:
. Teda muselo by platiť:
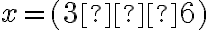 .
.
Rovnicu
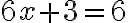 môžeme upraviť na tvar
môžeme upraviť na tvar
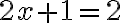 . Riešením tejto rovnice je podiel
. Riešením tejto rovnice je podiel
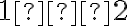 , teda
, teda
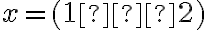 .
.
Zároveň vieme, že rovnica
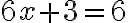 má nanajvýš jedno riešenie. Dokážte to!
má nanajvýš jedno riešenie. Dokážte to!
Rovnosť podielov
Racionálne čísla môžeme v určitom širšom význame chápať ako všetky možné podiely dvoch celých čísel.
Ukázali sme jednu podstatnú skutočnosť.
Ak „podiel“ celých čísel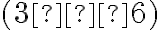 a zároveň aj podiel
a zároveň aj podiel
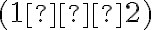 je hľadaným riešením rovnice, potom musí platiť rovnosť
je hľadaným riešením rovnice, potom musí platiť rovnosť
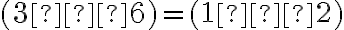 .
.
Ak použijeme označenie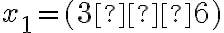 a
a
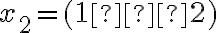 , tak je zrejmé, že
, tak je zrejmé, že
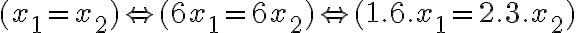 ).
).
Po vykrátení dostaneme rovnosť
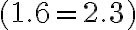 .
.
Ak „podiel“ celých čísel
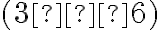 a zároveň aj podiel
a zároveň aj podiel
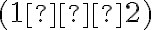 je hľadaným riešením rovnice, potom musí platiť rovnosť
je hľadaným riešením rovnice, potom musí platiť rovnosť
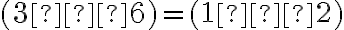 .
.
Ak použijeme označenie
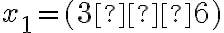 a
a
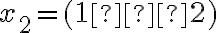 , tak je zrejmé, že
, tak je zrejmé, že
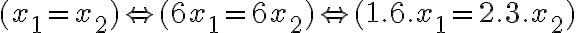 ).
).
Po vykrátení dostaneme rovnosť
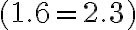 .
.
Rovnosť podielov dvoch celých čísel sme nahradili rovnosťou, kde sa vyskytuje len súčin celých čísel. Súčin je však neobmedzene definovaná operácia v obore celých čísel, t.j. vieme vynásobiť ľubovoľné dve celé čísla. Z uvedeného vyplýva, že racionálne
čísla môžeme zaviesť pomocou dvojíc celých čísel.
Porovnanie: celé a racionálne
V tejto kapitole nebudeme podrobne rozoberať postup definovania racionálnych čísel. Zameriame sa na vzájomný vzťah medzi zavedením množiny celých čísel a zavedením množiny racionálnych čísel.
Pri celých číslach sú východiskom prirodzené čísla a pri racionálnych číslach už môžeme použiť celé čísla! Relácia ekvivalencie pri celých číslach predstavuje „rozdiel“ prirodzených čísel a pri racionálnych číslach je to „podiel“ celých čísel.
Obor racionálnych čísel
Dve usporiadané dvojice prirodzených čísel
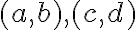 sú v relácii, ak platí rovnosť
sú v relácii, ak platí rovnosť
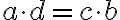 (súčin prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčinu prvého člena druhej dvojice s druhým členom prvej dvojice).
(súčin prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčinu prvého člena druhej dvojice s druhým členom prvej dvojice).
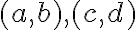 sú v relácii, ak platí rovnosť
sú v relácii, ak platí rovnosť
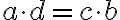 (súčin prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčinu prvého člena druhej dvojice s druhým členom prvej dvojice).
(súčin prvého člena prvej dvojice s druhým členom druhej dvojice sa rovná súčinu prvého člena druhej dvojice s druhým členom prvej dvojice).-
Nech
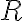 je binárna relácia s požadovanou vlastnosťou a nech
je binárna relácia s požadovanou vlastnosťou a nech
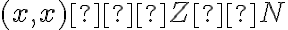 je ľubovoľná dvojica prirodzených čísel. Potom zrejme platí
je ľubovoľná dvojica prirodzených čísel. Potom zrejme platí
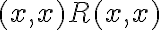 , lebo platí
, lebo platí
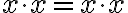 . Odkiaľ dostaneme, že relácia
. Odkiaľ dostaneme, že relácia
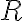 je reflexívna.
je reflexívna. - Nech ľubovoľné dve usporiadané dvojice sú v relácii
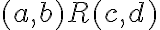 .
. - Rovnosť prirodzených čísel je symetrická, preto tiež platí:
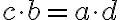 .
. - To je ekvivalentné so vzťahom
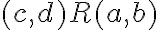 , preto platí: relácia
, preto platí: relácia
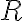 je symetrická.
je symetrická. - Nech platí
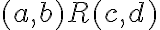 a zároveň
a zároveň
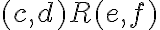 .
.
Triedy rozkladu
Úvahy o triedach rozkladu
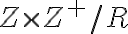 umožňujú zaviesť množinu racionálnych čísel ako množinu tried tohto rozkladu.
umožňujú zaviesť množinu racionálnych čísel ako množinu tried tohto rozkladu.
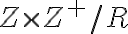 umožňujú zaviesť množinu racionálnych čísel ako množinu tried tohto rozkladu.
umožňujú zaviesť množinu racionálnych čísel ako množinu tried tohto rozkladu.
Zhrňme si naše úvahy:
Uvedieme definíciu množiny racionálnych čísel, ktorá vychádza z týchto úvah.
Súčet a súčin
Relácia ekvivalencie
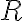 umožnila vytvorenie „nosiča“ pre racionálne čísla. Teraz musíme definovať súčet a súčin racionálnych čísel.
umožnila vytvorenie „nosiča“ pre racionálne čísla. Teraz musíme definovať súčet a súčin racionálnych čísel.
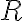 umožnila vytvorenie „nosiča“ pre racionálne čísla. Teraz musíme definovať súčet a súčin racionálnych čísel.
umožnila vytvorenie „nosiča“ pre racionálne čísla. Teraz musíme definovať súčet a súčin racionálnych čísel.
Nech
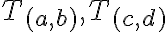 sú dve racionálne čísla (dve triedy rozkladu), potom súčet
sú dve racionálne čísla (dve triedy rozkladu), potom súčet
 a súčin
a súčin
 týchto čísel popisujú nasledujúce dve definície.
týchto čísel popisujú nasledujúce dve definície.
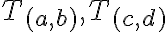 sú dve racionálne čísla (dve triedy rozkladu), potom súčet
sú dve racionálne čísla (dve triedy rozkladu), potom súčet
 a súčin
a súčin
 týchto čísel popisujú nasledujúce dve definície.
týchto čísel popisujú nasledujúce dve definície.Zvoľme si celé čísla
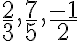 . Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
. Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
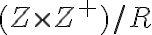 . Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
. Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
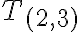 ≝
≝
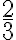 ,
,
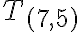 ,
≝
,
≝
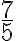 ,
,
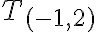 ≝
≝
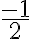 .
.
Interpretujme súčet (tried)
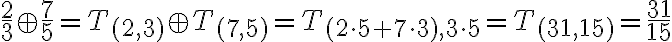
...
Interpretujte súčin tried
...
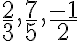 . Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
. Z definície množiny celých čísel vyplýva, že tieto čísla sú triedy rozkladu
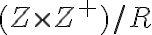 . Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
. Bez ujmy na všeobecnosti môžeme povedať, že platia vzťahy
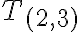 ≝
≝
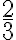 ,
,
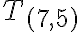 ,
≝
,
≝
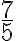 ,
,
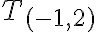 ≝
≝
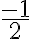 .
.
Interpretujme súčet (tried)
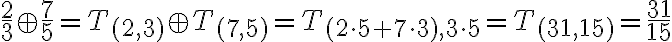
...
Interpretujte súčin tried
...
Poznámky.
Hustota racionálnych čísel
Nech
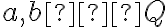 sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
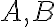 . Dokážte, že aritmetický priemer
. Dokážte, že aritmetický priemer
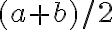 je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
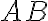 .
.
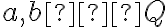 sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
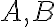 . Dokážte, že aritmetický priemer
. Dokážte, že aritmetický priemer
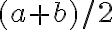 je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
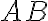 .
.
Nech 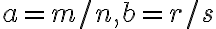 a zároveň
a zároveň
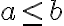
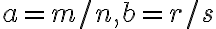 a zároveň
a zároveň
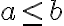
- Pre aritmetický priemer
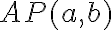 môžu nastať dva prípady:
môžu nastať dva prípady:
- Zlomok
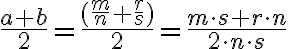 je v základnom tvare (nemožno ho krátiť).
je v základnom tvare (nemožno ho krátiť). - Zlomok
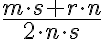 nie je v základnom tvare. Vtedy existuje nenulové prirodzené číslo
nie je v základnom tvare. Vtedy existuje nenulové prirodzené číslo
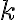 , ktorým zlomok vykrátime na základný tvar
, ktorým zlomok vykrátime na základný tvar
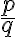 . Z vlastností o krátení zlomkov totiž musí platiť
. Z vlastností o krátení zlomkov totiž musí platiť
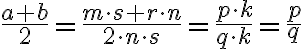 .
. - Z predchádzajúceho vyplýva, že zlomok
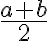 reprezentuje racionálne číslo, pre ktoré platí
reprezentuje racionálne číslo, pre ktoré platí
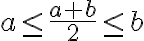
- Ukázať, že obraz aritmetického priemeru bude stred úsečky je jednoduché.
- K úplnosti dôkazu je potrebné ukázať, že platí rovnosť
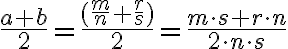
Nech
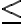 je relácia usporiadania na množine
je relácia usporiadania na množine
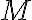 . Ak pre každé dva prvky
. Ak pre každé dva prvky
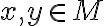 s vlastnosťou
s vlastnosťou
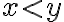 existuje prvok
existuje prvok
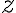 taký, že
taký, že
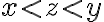 , tak množina
, tak množina
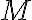 sa nazýva husto usporiadaná.
sa nazýva husto usporiadaná.
Keďže pre aritmetický priemer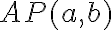 racionálnych čísel
racionálnych čísel
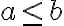 platí
platí
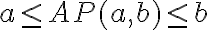 , tak platí aj nasledujúce tvrdenie:
, tak platí aj nasledujúce tvrdenie:
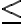 je relácia usporiadania na množine
je relácia usporiadania na množine
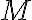 . Ak pre každé dva prvky
. Ak pre každé dva prvky
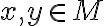 s vlastnosťou
s vlastnosťou
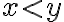 existuje prvok
existuje prvok
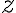 taký, že
taký, že
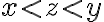 , tak množina
, tak množina
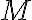 sa nazýva husto usporiadaná.
sa nazýva husto usporiadaná.
Keďže pre aritmetický priemer
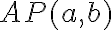 racionálnych čísel
racionálnych čísel
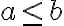 platí
platí
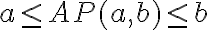 , tak platí aj nasledujúce tvrdenie:
, tak platí aj nasledujúce tvrdenie:
Množina racionálnych čísel je
husto usporiadaná.
Školská matematika
Racionálne čísla v školskej matematike zaádzame pomocou zlomkov, pričom dva zlomky
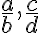 budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
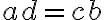 .
.
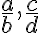 budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
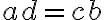 .
.
Množina racionálnych čísel je množina, ktorá obsahuje všetky zlomky, ktorých čitateľ je celé číslo a menovateľ je kladné prirodzené číslo.
Pri zavádzaní operácií sčítania a násobenia racionálnych čísel v školskej matematike sa opierame o sčítanie a násobenie zlomkov. Nech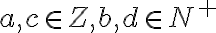 , potom v obore
, potom v obore
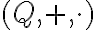 \) platí pre:
\) platí pre:
Pri zavádzaní operácií sčítania a násobenia racionálnych čísel v školskej matematike sa opierame o sčítanie a násobenie zlomkov. Nech
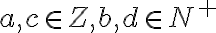 , potom v obore
, potom v obore
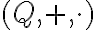 \) platí pre:
\) platí pre:
Poznámky.
- Pri sčitovaní zlomkov s rôznymi znamienkami niekedy žiaci "kopírujú" postup pre odčítanie celých čísel.
- Napríklad pri súčte
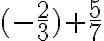 skúmajú, ktoré z čísel
skúmajú, ktoré z čísel
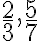 je väčšie.
je väčšie.
- Obor
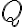 racionálnych čísel je množina všetkých zlomkov
racionálnych čísel je množina všetkých zlomkov
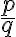 , kde
, kde
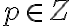 a
a
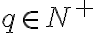 , na ktorej sú definované operácie sčítania a násobenia.
, na ktorej sú definované operácie sčítania a násobenia. -
V prípade, že čísla
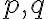 sú nesúdeliteľné (ich najväčší spoločný deliteľ je rovný
sú nesúdeliteľné (ich najväčší spoločný deliteľ je rovný
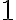 ), hovoríme že zlomok
), hovoríme že zlomok
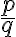 je v základnom tvare.
je v základnom tvare. - Množinu racionálnych čísel môžeme reprezentovať všetkými zlomkami, ktoré sú v základnom tvare.
-
Mimochodom sú to aj všetky celé čísla, lebo pre
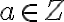 je zlomok
je zlomok
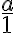 v základnom tvare a teda reprezentuje racionálne číslo.
v základnom tvare a teda reprezentuje racionálne číslo.
Vytvorte alebo nájdite vhodný applet, ktorý vám pomôže zodpovedať otázky:
Ako sa mení hodnota zlomku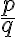 , keď zväčšujeme číslo
, keď zväčšujeme číslo
 ?
?
Ako ovplyvňuje hodnotu zlomku zväčšenie menovateľa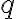 ?
?
Pozrite si knihu appletov ku zlomkom Tu a v nej kapitolu Fractions on a numberline
Ako sa mení hodnota zlomku
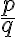 , keď zväčšujeme číslo
, keď zväčšujeme číslo
 ?
?
Ako ovplyvňuje hodnotu zlomku zväčšenie menovateľa
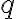 ?
?
Pozrite si knihu appletov ku zlomkom Tu a v nej kapitolu Fractions on a numberline