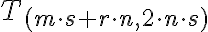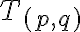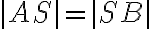Celé čísla a racionálne čísla
celé čísla
Obor racionálnych čísel
Hustota racionálnych čísel
Nech
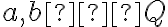 sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
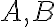 . Dokážte, že aritmetický priemer
. Dokážte, že aritmetický priemer
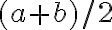 je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
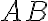 .
.
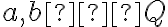 sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
sú dve rôzne racionálne čísla a ich reprezentácie na číselnej osi nech sú body
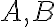 . Dokážte, že aritmetický priemer
. Dokážte, že aritmetický priemer
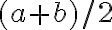 je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
je opäť racionálne číslo a jeho obraz na číselnej osi je stred úsečky
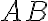 .
.
Nech 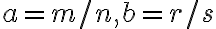 a zároveň
a zároveň
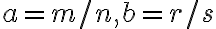 a zároveň
a zároveň
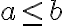
- Pre aritmetický priemer
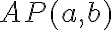 môžu nastať dva prípady:
môžu nastať dva prípady:
- Zlomok
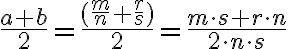 je v základnom tvare (nemožno ho krátiť).
je v základnom tvare (nemožno ho krátiť). - Zlomok
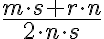 nie je v základnom tvare. Vtedy existuje nenulové prirodzené číslo
nie je v základnom tvare. Vtedy existuje nenulové prirodzené číslo
 , ktorým zlomok vykrátime na základný tvar
, ktorým zlomok vykrátime na základný tvar
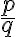 . Z vlastností o krátení zlomkov totiž musí platiť
. Z vlastností o krátení zlomkov totiž musí platiť
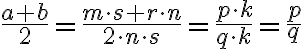 .
. - Z predchádzajúceho vyplýva, že zlomok
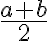 reprezentuje racionálne číslo, pre ktoré platí
reprezentuje racionálne číslo, pre ktoré platí
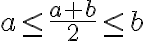
- Ukázať, že obraz aritmetického priemeru bude stred úsečky je jednoduché.
- K úplnosti dôkazu je potrebné ukázať, že platí rovnosť
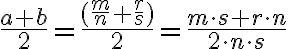
Nech
 je relácia usporiadania na množine
je relácia usporiadania na množine
 . Ak pre každé dva prvky
. Ak pre každé dva prvky
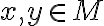 s vlastnosťou
s vlastnosťou
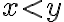 existuje prvok
existuje prvok
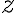 taký, že
taký, že
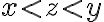 , tak množina
, tak množina
 sa nazýva husto usporiadaná.
sa nazýva husto usporiadaná.
Keďže pre aritmetický priemer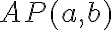 racionálnych čísel
racionálnych čísel
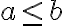 platí
platí
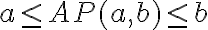 , tak platí aj nasledujúce tvrdenie:
, tak platí aj nasledujúce tvrdenie:
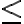 je relácia usporiadania na množine
je relácia usporiadania na množine
 . Ak pre každé dva prvky
. Ak pre každé dva prvky
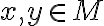 s vlastnosťou
s vlastnosťou
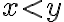 existuje prvok
existuje prvok
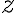 taký, že
taký, že
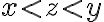 , tak množina
, tak množina
 sa nazýva husto usporiadaná.
sa nazýva husto usporiadaná.
Keďže pre aritmetický priemer
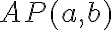 racionálnych čísel
racionálnych čísel
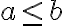 platí
platí
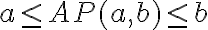 , tak platí aj nasledujúce tvrdenie:
, tak platí aj nasledujúce tvrdenie:
Množina racionálnych čísel je
husto usporiadaná.