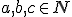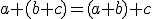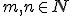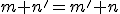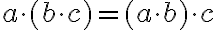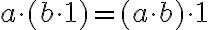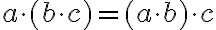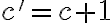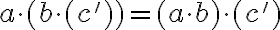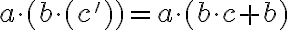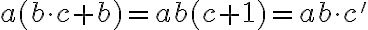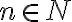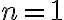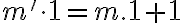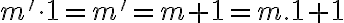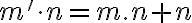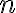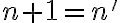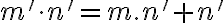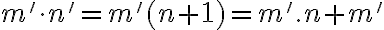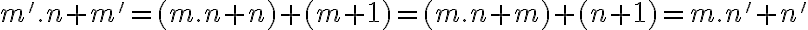Konštrukcia číselných oborov - prirodzené čísla
Vlastnosti operácií
Asociatívnosť
Dôkaz.
Budeme dokazovať matematickou indukciou vzhľadom na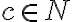 .
.
Budeme dokazovať matematickou indukciou vzhľadom na
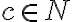 .
.- Pre
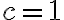 musíme ukázať, že platí rovnosť
musíme ukázať, že platí rovnosť
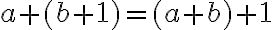 Pre ľavú stranu po úprave dostaneme
Pre ľavú stranu po úprave dostaneme
-
Predpokladajme, že rovnosť
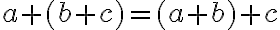 platí pre prirodzené číslo
platí pre prirodzené číslo
 .
Ukážeme, že platí aj pre
.
Ukážeme, že platí aj pre
- Podľa indukčného predpokladu a axiómy III sa bude ľavá strana rovnať pravej strane
- Tým je dôkaz ukončený.
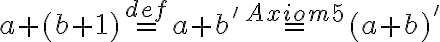 .
.
Pre pravú stranu z definície následníka dostaneme
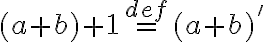 .
.
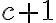 , čo je ekvivalentné s rovnosťou
, čo je ekvivalentné s rovnosťou
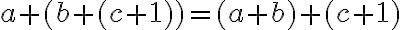 .
.
Pre pravú stranu po úprave dostaneme
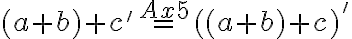
pre ľavú stranu dostaneme
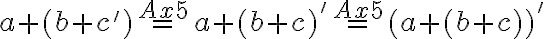
Dôkaz.
Budeme dokazovať matematickou indukciou vzhľadom na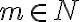
Budeme dokazovať matematickou indukciou vzhľadom na
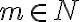
- Pre
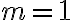 zrejme platí rovnosť
zrejme platí rovnosť
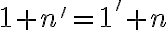 lebo
lebo
Pre ľavú stranu po úprave dostaneme
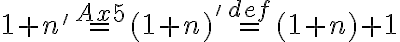
Využitím komutatívnosti (Veta 3) pre ľubovoľné prirodzené číslo a asociatívnosti (Veta 5)
a asociatívnosti (Veta 5)
dostaneme
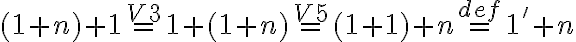
-
Predpokladajme (i.p.), že rovnosť
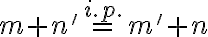 platí pre prirodzené číslo
platí pre prirodzené číslo
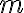 .
.
Ukážeme, že platí aj pre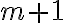 , , čo je ekvivalentné s rovnosťou
, , čo je ekvivalentné s rovnosťou
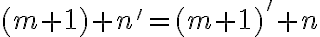 .
.
Pre pravú stranu po úprave dostaneme
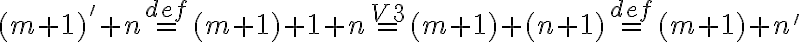
- To znamená, že pravá strana sa rovná ľavej. Tým je dôkaz ukončený.
Poznámky.
1) Distributívnosť násobenia zľava k sčítaniu ľahko dokážeme pomocou matematickej indukcie priamo zo VII. axiómy.
2) O distributívnosti násobenia sprava k sčítaniu hovorí nasledujúca veta.
1) Distributívnosť násobenia zľava k sčítaniu ľahko dokážeme pomocou matematickej indukcie priamo zo VII. axiómy.
2) O distributívnosti násobenia sprava k sčítaniu hovorí nasledujúca veta.