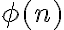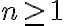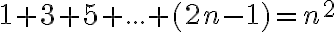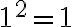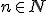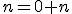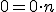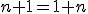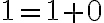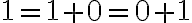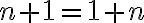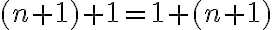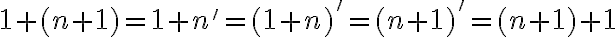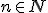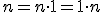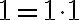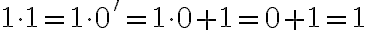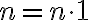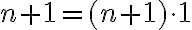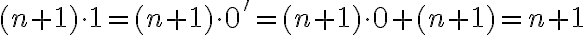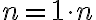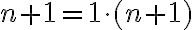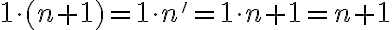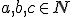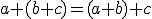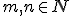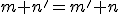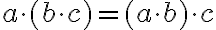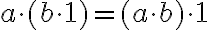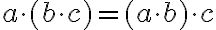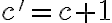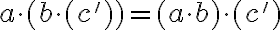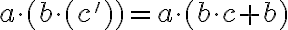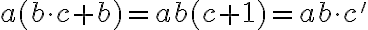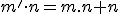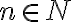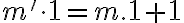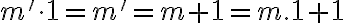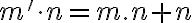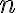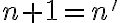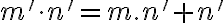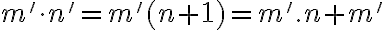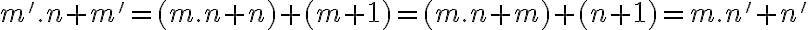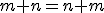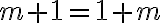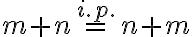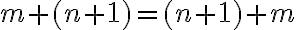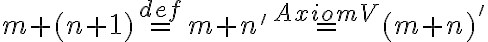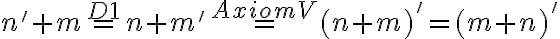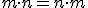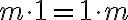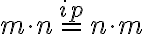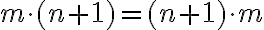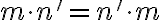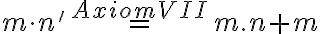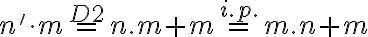Konštrukcia číselných oborov - prirodzené čísla
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Konštrukcia číselných oborov - prirodzené čísla |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 15:24 |
Číselné obory
Historický vývoj
Prirodzené čísla si ľudia utvárali pri skúmaní vzťahov medzi skupinami reálnych objektov. Pri skúmaní vzťahov medzi skupinami objektov sa abstrahovalo od veľkosti, farby a ďalších vlastností, ale podstatné bolo len to, či
predmety dvoch súborov možno zoradiť do dvojíc.
Za najdôležitejšie zistenie pri „počítaní objektov“ bol objav ľudstva, pomocou ktorého dokázali odpovedať na otázku:
Za najdôležitejšie zistenie pri „počítaní objektov“ bol objav ľudstva, pomocou ktorého dokázali odpovedať na otázku:
V ktorej skupine je menej, viac resp. rovnako objektov?
Z histórie vývoja matematiky sú známe tzv.
vrubovky
,
ktoré slúžili na primitívne určovanie počtu prvkov v skupine. Jedna z najstarších vruboviek bola objavená na Morave v roku 1936.
V siedmom storočí nášho letopočtu indo-arabská matematika zaviedla desiatkovú číselnú sústavu.
Napriek takýmto významným pokrokom sa mnoho storočí nedarilo vytvoriť axiomatickú teóriu prirodzených čísel. Pokusy spracovať aj teóriu prirodzených čísel axiomaticky boli neúspešné viac ako dve tisíc rokov.
V siedmom storočí nášho letopočtu indo-arabská matematika zaviedla desiatkovú číselnú sústavu.
Napriek takýmto významným pokrokom sa mnoho storočí nedarilo vytvoriť axiomatickú teóriu prirodzených čísel. Pokusy spracovať aj teóriu prirodzených čísel axiomaticky boli neúspešné viac ako dve tisíc rokov.
Pokusy spracovať aj teóriu prirodzených čísel axiomaticky
boli neúspešné viac ako dve tisíc rokov.
Ani zavedenie desiatkovej číselnej sústavy v 7. storočí ani značný pokrok v oblasti aritmetiky v 12. až 19. storočí, matematikom sa nedarilo vytvoriť axiomatickú teóriu prirodzených čísel.
Geometriu pritom axiomaticky spracoval už Euklides vo svojich Základoch okolo roku 300 pred Kristom. Dokonca Leopold Kronecker (nemecký matematik 1823 - 1891) pri jednej prednáške roku 1886 povedal slávnu vetu:
Geometriu pritom axiomaticky spracoval už Euklides vo svojich Základoch okolo roku 300 pred Kristom. Dokonca Leopold Kronecker (nemecký matematik 1823 - 1891) pri jednej prednáške roku 1886 povedal slávnu vetu:
Boh stvoril prirodzené čísla, všetko ostatné je ľudské dielo.1)
Tieto problémy vyriešil až v 20. storočí G. Peano, ktorý zaviedol prirodzené čísla axiomaticky. Giuseppe Peano (1858 - 1932) bol taliansky matematik,
filozof a logik. Bol jedným zo zakladateľov modernej matematickej logiky a výrazne sa podieľal na vzniku teórie množín. Jeho veľkým prínosom pre aritmetiku bol axiomatický prístup zavedenia oboru prirodzených čísel, ktorý budeme na jeho počesť nazývať Peanova aritmetika
.
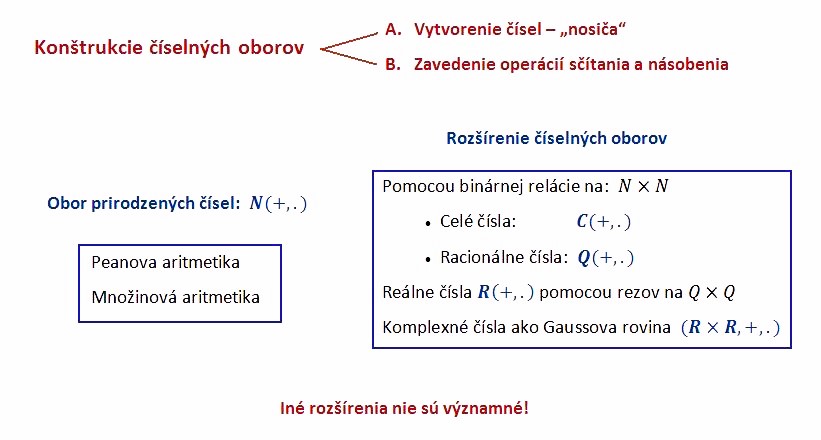
Teoretická aritmetika pri zavadzaní a rozširovaní číselných oborov kladie dôraz predovšetkým na:
- Konštrukciu („vytvorenie“) číselnej množiny („nosiča“).
- Zavedenie operácií sčítania a násobenia na tejto množine.
- Popísanie základných vlastností aritmetických operácií.
Zavedenie nového číselného oboru znamená, že v prvom rade musíme
1) E. T. Bell, Men of Mathematics. New York 1986, str. 477.
- upopísať spôsob ako vytvoríme konkrétny typ čísla.
- začneme vytvorením množiny prirodzených čísel.
- pri každej ďalšej konštrukcii nového číselného oboru budeme už vychádzať zo známych číselných oborov.
Príklad rozšírenia
Nech 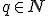 je ľubovoľné prirodzené číslo rôzne od nuly a
je ľubovoľné prirodzené číslo rôzne od nuly a 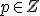 je ľubovoľné celé číslo. Množinu racionálnych
čísel
je ľubovoľné celé číslo. Množinu racionálnych
čísel 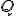 môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
Takéto dvojice![\small [p,q] \small [p,q]](https://lms.umb.sk/filter/tex/pix.php/f638a7987a9a0506caf6e3e19494ee83.png) môžeme interpretovať aj ako zlomky
môžeme interpretovať aj ako zlomky 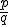 .
.
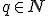 je ľubovoľné prirodzené číslo rôzne od nuly a
je ľubovoľné prirodzené číslo rôzne od nuly a 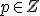 je ľubovoľné celé číslo. Množinu racionálnych
čísel
je ľubovoľné celé číslo. Množinu racionálnych
čísel 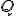 môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
môžeme zaviesť pomocou relácie ekvivalencie na množine všetkých usporiadaných dvojíc celých čísel.
Takéto dvojice
![\small [p,q] \small [p,q]](https://lms.umb.sk/filter/tex/pix.php/f638a7987a9a0506caf6e3e19494ee83.png) môžeme interpretovať aj ako zlomky
môžeme interpretovať aj ako zlomky 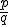 .
.
- Na množine zlomkov
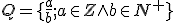 potom definujme rovnosť zlomkov takto:
potom definujme rovnosť zlomkov takto:
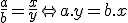
- Ukážte, že rovnosť zlomkov je relácia ekvivalencie, ktorá množinu všetkých zlomkov rozdelí do disjunktných podmnožín.
- Popíšte tento rozklad.
- Napríklad trieda rozkladu, ktorá obsahuje zlomok
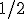 bude obsahovať aj zlomky
bude obsahovať aj zlomky 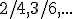 .
. - Všetky zlomky z tejto podmnožiny sa navzájom rovnajú.
- Preto stačí vybrať jeden zlomok, ktorý bude reprezentovať túto podmnožinu a vyhlásiť ho za racionálne číslo.
- Za „reprezentanta“ racionálneho čísla zvolíme každý zlomok
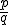 , ktorý je v základnom tvare. Teda, keď čísla
, ktorý je v základnom tvare. Teda, keď čísla
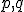 sú nesúdeliteľné a zárove
sú nesúdeliteľné a zárove 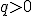 . Inými slovami, ak zlomok
. Inými slovami, ak zlomok 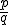 už nemôžeme krátiť.
už nemôžeme krátiť. - Množina racionálnych čísel
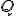 je množina všetkých zlomkov v základnom tvare.
je množina všetkých zlomkov v základnom tvare.
Uveďme aj matematický zápis takejto množiny: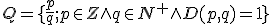
- Operácie sčítanie a násobenie racionálnych čísel potom môžeme zaviesť pomocou pravidiel na súčet a súčin zlomkov. Definujte tieto operácie.
Poznámka.
Takýto spôsob zavedenia racionálnych čísel pomocou zlomkov je vhodný pre školskú matematiku, keďže žiaci sa oboznamujú najskôr so zlomkami. Pozri Fraction Book.
Takýto spôsob zavedenia racionálnych čísel pomocou zlomkov je vhodný pre školskú matematiku, keďže žiaci sa oboznamujú najskôr so zlomkami. Pozri Fraction Book.
Peanova aritmetika
Východiskovým pojmom Peanovej aritmetiky je prirodzené číslo.
Prirodzené číslo nedefinujeme, podobne ako v euklidovskej geometrii nedefinujeme bod. Takéto východisko pripomína Kroneckerov výrok, že prirodzené sú dané vopred a mi im pripisujeme len nejaké vlastnosti.
Peanova aritmetika si kladie za cieľ vedecky popísať vnútornú štruktúru množiny všetkých prirodzených čísel a zároveň popísať operácie sčítanie a násobenie na tejto množine.
Peanova aritmetika si kladie za cieľ vedecky popísať vnútornú štruktúru množiny všetkých prirodzených čísel a zároveň popísať operácie sčítanie a násobenie na tejto množine.
Axiómy rozdelíme do štyroch skupín:
- Prvá skupina sa viaže na existenciu množiny prirodzených čísel.
- Druhá skupina definuje binárnu operáciu sčítanie.
- Tretia skupina definuje binárnu operáciu násobenie.
- V štvrtá skupina popisuje princíp matematickej indukcie.
Poznámka.
Giuseppe Peano (1858 - 1932) bol taliansky matematik, bol jedným zo zakladateľov modernej matematickej logiky a podieľal sa na vzniku teórie množín.
Jeho veľkým prínosom pre aritmetiku bol axiomatický prístup zavedenia oboru prirodzených čísel, ktorý dnes nazývame Peanova aritmetika.
Giuseppe Peano (1858 - 1932) bol taliansky matematik, bol jedným zo zakladateľov modernej matematickej logiky a podieľal sa na vzniku teórie množín.
Jeho veľkým prínosom pre aritmetiku bol axiomatický prístup zavedenia oboru prirodzených čísel, ktorý dnes nazývame Peanova aritmetika.
Druhá skupina
Súčet dvoch prirodzených čísel spĺňa nasledujúce dve -
axiómy
Poznámky.
Tretia skupina
Definícia.
Súčin - ku každým dvom prirodzeným číslam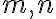 existuje prirodzené číslo
existuje prirodzené číslo
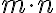 nazývané súčin týchto čísel .
nazývané súčin týchto čísel .
Súčin - ku každým dvom prirodzeným číslam
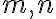 existuje prirodzené číslo
existuje prirodzené číslo
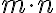 nazývané súčin týchto čísel .
nazývané súčin týchto čísel .
Súčin dvoch prirodzených čísel spĺňa nasledujúce dve -
axiómy
Poznámky.
- Axióma VII je rekurentným matematickým vyjadrením, umožňuje násobiť prirodzené čísla neobmedzene.
- Podobne ako pri súčte, axiómy VI a VII definujú súčin ľubovoľného prirodzeného čísla a nuly resp. nasledovníka.
- V axióme VII je skrytý súčin
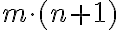 , ktorý v súlade s pravidlami v matematike (distributívnosť) chceme,
aby sa rovnal súčtu
, ktorý v súlade s pravidlami v matematike (distributívnosť) chceme,
aby sa rovnal súčtu 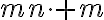 .
.
Riešenie
Matematická indukcia
Definícia.
Matematická indukcia
Matematická indukcia
Axióma VIII
Ak
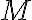 je množina prirodzených čísel, ktorá obsahuje nulu
je množina prirodzených čísel, ktorá obsahuje nulu
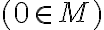 a zároveň pre každé prirodzené číslo
a zároveň pre každé prirodzené číslo 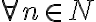 platí:
platí:
[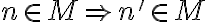 ] potom
] potom
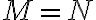 .
.
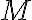 je množina prirodzených čísel, ktorá obsahuje nulu
je množina prirodzených čísel, ktorá obsahuje nulu
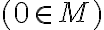 a zároveň pre každé prirodzené číslo
a zároveň pre každé prirodzené číslo 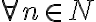 platí:
platí:
[
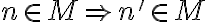 ] potom
] potom
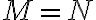 .
.
Poznámka.
Axiómu VIII môžeme formulovať aj pomocou jazyka výrokovej logiky.
Axiómu VIII môžeme formulovať aj pomocou jazyka výrokovej logiky.
Vlastnosti operácií
Dôkaz.
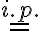 .
.
- Pre
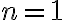 musíme ukázať, že platí rovnosť:
musíme ukázať, že platí rovnosť:
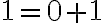 .
.
Upravujme pravú stranu rovnosti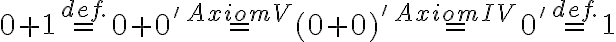 ,
,
čo je ľavá strana rovnosti. -
Predpokladajme (i.p.), že rovnosť
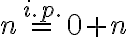 platí pre prirodzené číslo
platí pre prirodzené číslo
 .
.
Musíme ukázať, že platí aj pre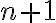 , čo je ekvivalentné s rovnosťou
, čo je ekvivalentné s rovnosťou
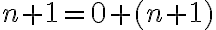 . (1)
Zrejme pre ľavú stranu rovnosti (1) platí
. (1)
Zrejme pre ľavú stranu rovnosti (1) platí
- Zároveň úpravou pravej strany rovnosti (1) dostaneme
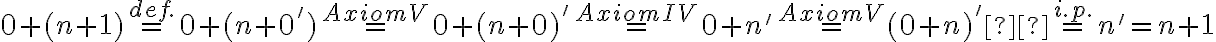 .
.
- Tým je dôkaz ukončený.
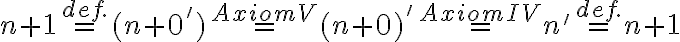 .
.
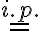 .
.
Dôkaz
- Pre
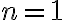 musíme ukázať, že platí rovnosť:
musíme ukázať, že platí rovnosť:
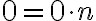 . Z axiómy VI vieme, že platí
. Z axiómy VI vieme, že platí
- Predpokladajme (i.p.), že rovnosť
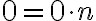 platí pre prirodzené číslo
platí pre prirodzené číslo
 . Musíme ukázať, že platí aj pre
. Musíme ukázať, že platí aj pre
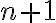 :
:
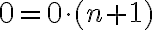 .
.
Upravujme pravú stranu rovnosti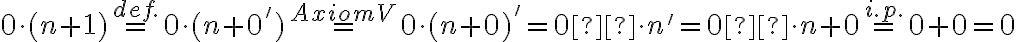 .
.
- Tým je dôkaz ukončený.
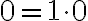 .
.
Jednotka je nasledovník nuly, teda platí
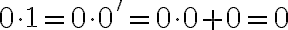 . Teda násobenie nuly a jednotky je komutatívne
. Teda násobenie nuly a jednotky je komutatívne
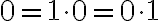 .
.
Dôkaz.
Asociatívnosť
Dôkaz.
Budeme dokazovať matematickou indukciou vzhľadom na .
.
Budeme dokazovať matematickou indukciou vzhľadom na
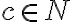 .
.- Pre
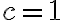 musíme ukázať, že platí rovnosť
musíme ukázať, že platí rovnosť
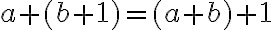 Pre ľavú stranu po úprave dostaneme
Pre ľavú stranu po úprave dostaneme
-
Predpokladajme, že rovnosť
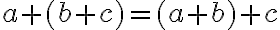 platí pre prirodzené číslo
platí pre prirodzené číslo
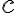 .
Ukážeme, že platí aj pre
.
Ukážeme, že platí aj pre
- Podľa indukčného predpokladu a axiómy III sa bude ľavá strana rovnať pravej strane
- Tým je dôkaz ukončený.
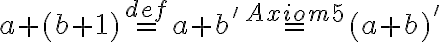 .
.
Pre pravú stranu z definície následníka dostaneme
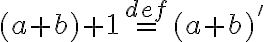 .
.
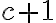 , čo je ekvivalentné s rovnosťou
, čo je ekvivalentné s rovnosťou
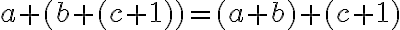 .
.
Pre pravú stranu po úprave dostaneme
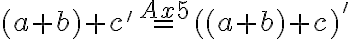
pre ľavú stranu dostaneme
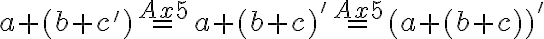
Dôkaz.
Budeme dokazovať matematickou indukciou vzhľadom na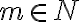
Budeme dokazovať matematickou indukciou vzhľadom na
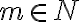
- Pre
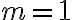 zrejme platí rovnosť
zrejme platí rovnosť
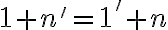 lebo
lebo
Pre ľavú stranu po úprave dostaneme
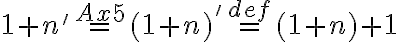
Využitím komutatívnosti (Veta 3) pre ľubovoľné prirodzené číslo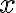 a asociatívnosti (Veta 5)
a asociatívnosti (Veta 5)
dostaneme
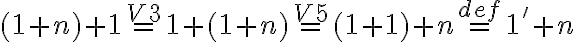
-
Predpokladajme (i.p.), že rovnosť
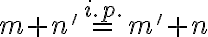 platí pre prirodzené číslo
platí pre prirodzené číslo
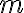 .
.
Ukážeme, že platí aj pre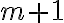 , , čo je ekvivalentné s rovnosťou
, , čo je ekvivalentné s rovnosťou
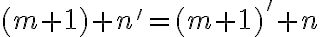 .
.
Pre pravú stranu po úprave dostaneme
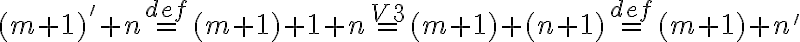
- To znamená, že pravá strana sa rovná ľavej. Tým je dôkaz ukončený.
Poznámky.
1) Distributívnosť násobenia zľava k sčítaniu ľahko dokážeme pomocou matematickej indukcie priamo zo VII. axiómy.
2) O distributívnosti násobenia sprava k sčítaniu hovorí nasledujúca veta.
1) Distributívnosť násobenia zľava k sčítaniu ľahko dokážeme pomocou matematickej indukcie priamo zo VII. axiómy.
2) O distributívnosti násobenia sprava k sčítaniu hovorí nasledujúca veta.
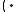
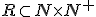
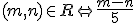
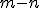
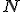
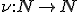
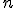
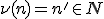
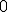
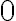
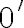
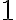
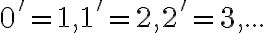
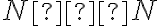
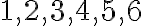
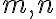
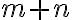
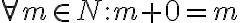
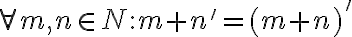
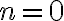
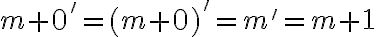
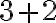
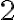
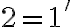
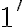
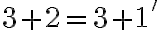
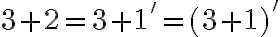
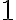
![3+2=(3+0')'=[(3+0)']'=[3']'=4'=5 3+2=(3+0')'=[(3+0)']'=[3']'=4'=5](https://lms.umb.sk/filter/tex/pix.php/74faa4e39388e3b1079cebb1d8b8ecf5.png)
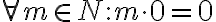
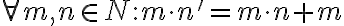
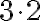
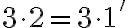
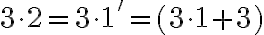
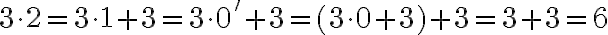
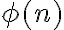
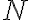
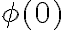
![[\forall n (\phi (n) \Rightarrow \phi (n'))] [\forall n (\phi (n) \Rightarrow \phi (n'))]](https://lms.umb.sk/filter/tex/pix.php/847f7e70c0564b16e8f274d38185af53.png)