Číselné obory na základných a stredných školách
Číselné obory na základných a stredných školách
Reálne čísla
Pytagorova škola
Matematik Pytagorovej školy Hippasus (5. stor. pred n. l.) ukázal, že uhlopriečka štvorca s jednotkovou stranou nemôže byť vyjadrená racionálnym číslom1)
Hippasus pravdepodobne dospel k záveru, že
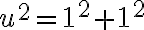 a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi
a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi 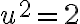 .
.
S využitím vlastností deliteľnosti ukážeme, že táto rovnica nemá v obore racionálnych čísel
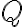 riešenie.
riešenie.
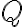 riešenie.
riešenie.
Dokážeme to nepriamo.
Nech existuje racionálne číslo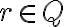 , ktoré je riešením rovnice
, ktoré je riešením rovnice 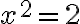 . Potom zrejme
. Potom zrejme
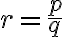 , pričom celé čísla
, pričom celé čísla
 sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
 je rovný
je rovný
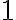 .
.
Po dosadení do rovnice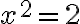 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť
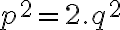 . Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
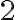 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
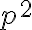 je párne, preto musí byť aj číslo
je párne, preto musí byť aj číslo
 párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare
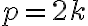 . Po dosadení do rovnosti
. Po dosadení do rovnosti
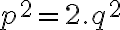 dostávame
dostávame
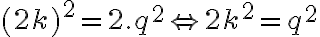 .
.
Analogickou úvahou zistíme, že číslo je párne. Keďže aj číslo
je párne. Keďže aj číslo
 je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel
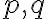 je väčší alebo rovný číslu
je väčší alebo rovný číslu
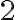 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo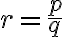 , kde
, kde
 sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
Nech existuje racionálne číslo
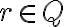 , ktoré je riešením rovnice
, ktoré je riešením rovnice 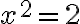 . Potom zrejme
. Potom zrejme
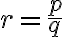 , pričom celé čísla
, pričom celé čísla
 sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
 je rovný
je rovný
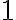 .
.
Po dosadení do rovnice
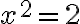 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť
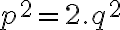 . Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
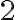 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
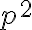 je párne, preto musí byť aj číslo
je párne, preto musí byť aj číslo
 párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare
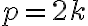 . Po dosadení do rovnosti
. Po dosadení do rovnosti
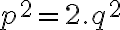 dostávame
dostávame
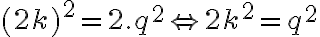 .
.
Analogickou úvahou zistíme, že číslo
 je párne. Keďže aj číslo
je párne. Keďže aj číslo
 je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel
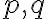 je väčší alebo rovný číslu
je väčší alebo rovný číslu
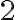 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo
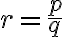 , kde
, kde
 sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
___________________________________________________________________________________________
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
