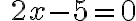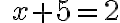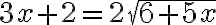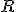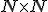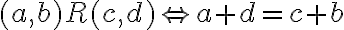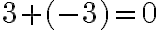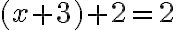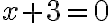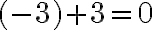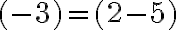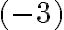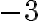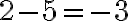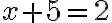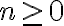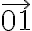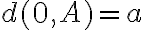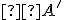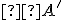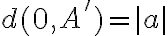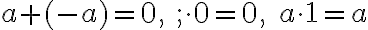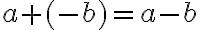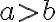Číselné obory na základných a stredných školách
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Číselné obory na základných a stredných školách |
| Vytlačil(a): | Guest user |
| Dátum: | streda, 3 júla 2024, 13:34 |
Opis
Číselné obory na základných a stredných školách
Úvod
Číselný obor je množina čísel (číselná množina), na ktorej sú zavedené základné aritmetické operácie: sčítanie a násobenie. Číselné obory zavádzame postupne:
- Na 1. stupni ZŠ začíname oborom prirodzených čísel, ktorý na 2. stupni ZŠ rozšírime na obor celých čísel.
- Obor celých čísel rozšírime na obor racionálnych a obor racionálnych na obor reálnych čísel.
- Nakoniec ale až na SŠ zavedieme komplexné čísla ako množinu všetkých usporiadaných dvojíc reálnych čísel, na ktorej vhodne definujeme sčítanie a násobenie.
Otvorte si applet Tu
Potrebu rozširovania číselných oborov môžeme demonštrovať na riešení rovníc.
- Na prvom stupni ZŠ
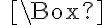
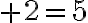
Pri riešení rovníc tohto typu žiaci používajú metódu priameho dosadzovania/zapisovania. Do rámika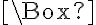 vpisujú prirodzené čísla a zisťujú, či vzniknutá rovnosť platí.
vpisujú prirodzené čísla a zisťujú, či vzniknutá rovnosť platí.
Na tomto stupni vzdelávania základnou metódou pri riešení jednoduchých lineárnych rovníc je experimentálna metóda. - Na druhom stupni ZŠ
- Na strednej škole
-
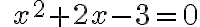
Pri riešení kvadratických rovníc žiaci 1. ročníka SŠ využívajú okrem ekvivalentných úprav aj
vzorce pre výpočet koreňov kvadratických rovníc. Pozrite si applet Tu. -
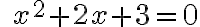
Pri riešení kvadratických rovníc so záporným diskriminantom žiaci SŠ musia poznať komplexné čísla.
-
Celé čísla
Jedna z náročných ale zároveň dôležitých etáp pri rozširovaní číselných oborov na základnej škole je rozšírenie oboru prirodzených čísle na obor celých čísel.
Zavedenie oboru celých čísel je v súčasnosti zakotvené v učebných osnovách pre 8. ročník ZŠ. Východiskovým pojmom je opačné číslo.
Prv než začneme s charakteristikou procesu výstavby celých čísel na ZŠ a komparáciou učebníc matematiky používaných na ZŠ, uvedieme teoretické východiská k tejto problematike.
Motiváciou pri zavádzaní celých čísel môže byť problém, ktorý nastane pri pokuse riešiť niektoré lineárne rovnice v obore prirodzených čísel. Napríklad:
Prv než začneme s charakteristikou procesu výstavby celých čísel na ZŠ a komparáciou učebníc matematiky používaných na ZŠ, uvedieme teoretické východiská k tejto problematike.
Motiváciou pri zavádzaní celých čísel môže byť problém, ktorý nastane pri pokuse riešiť niektoré lineárne rovnice v obore prirodzených čísel. Napríklad:
Jednoduchá algebraická rovnica 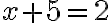 , ktorej koeficienty
, ktorej koeficienty 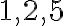 sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
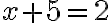 , ktorej koeficienty
, ktorej koeficienty 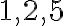 sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
- Ak budeme aplikovať ekvivalentnú úpravu „odčítanie“ čísla
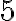 k obidvom stranám rovnice, tak dostaneme
k obidvom stranám rovnice, tak dostaneme 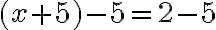 .
. - Po úprave na ľavej strane rovnice dostaneme
 a na pravej strane dostanem riešenie v tvare
a na pravej strane dostanem riešenie v tvare  .
. - Veľmi ľahko sa presvedčíme, že rozdiel
 v obore prirodzených čísle neexistuje. Preto je nutné vytvoriť číselný obor, v ktorom takýto rozdiel existuje.
v obore prirodzených čísle neexistuje. Preto je nutné vytvoriť číselný obor, v ktorom takýto rozdiel existuje. - Myšlienka vytvorenia nového číselného oboru pomocou "rozdielov dvoch prirodzených čísel" je nosnou pri zavádzaní oboru celých čísel v teoretickej aritmetike na VŠ.
Vysoká škola - teoretická aritmetika
Na začiatku je vhodné (aj keď nie nutné) zaviesť pojem opačného čísla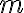 k ľubovoľnému prirodzenému číslu
k ľubovoľnému prirodzenému číslu  , ktoré sa definuje pomocou rovnosti
, ktoré sa definuje pomocou rovnosti
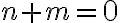 .
.
Celé čísla zavedieme pomocou vhodnej relácie ekvivalencie a rozkladu karteziánskeho súčinu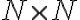 množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
Pozrite si vlastnosti tejto relácie Tu
Na začiatku je vhodné (aj keď nie nutné) zaviesť pojem opačného čísla
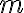 k ľubovoľnému prirodzenému číslu
k ľubovoľnému prirodzenému číslu  , ktoré sa definuje pomocou rovnosti
, ktoré sa definuje pomocou rovnosti
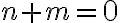 .
.
Celé čísla zavedieme pomocou vhodnej relácie ekvivalencie a rozkladu karteziánskeho súčinu
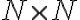 množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
Nech 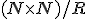 je rozklad karteziánskeho súčinu
je rozklad karteziánskeho súčinu 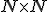 , potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel
, potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel 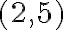 a
a 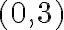 patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo
patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo 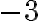 .
.
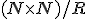 je rozklad karteziánskeho súčinu
je rozklad karteziánskeho súčinu 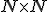 , potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel
, potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel 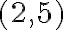 a
a 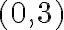 patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo
patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo 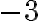 .
.
Vráťme sa teraz do 8. ročníka základnej školy a pokúsme sa vyriešiť rovnicu 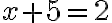 .
.
Pri jej riešení môžeme použiť aj nasledovný postup: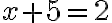 Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi:
Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi: 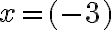 resp.
resp. 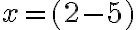 .
.
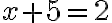 .
.Pri jej riešení môžeme použiť aj nasledovný postup:
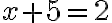 Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi:
Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi: 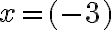 resp.
resp. 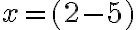 .
.
Závery:
Historické pozadie
Záporné čísla sa objavili po prvýkrát v čínskej matematike. V knihe „Deväť kapitol matematického umenia“ (202 pred n.l.) sú použité červené „úsečky“ pre kladné čísla a čierne pre záporné čísla.
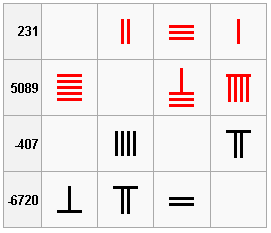
Tento systém je opak súčasného zapisovania kladných a záporných čísel v oblasti bankovníctva, účtovníctva a obchode.
Záporné čísla sa objavili po prvýkrát v čínskej matematike. V knihe „Deväť kapitol matematického umenia“ (202 pred n.l.) sú použité červené „úsečky“ pre kladné čísla a čierne pre záporné čísla.

Tento systém je opak súčasného zapisovania kladných a záporných čísel v oblasti bankovníctva, účtovníctva a obchode.
- V 7. storočí nášho letopočtu v Indii, boli záporné čísla použité na vyjadrenie dlhu. Indický matematik Brahmagupta, uvádza pravidlá pre operácie sčítania a násobenia so zápornými číslami. Používal termíny "dlh“ a „úver“.
- Európski matematici sa bránili konceptu záporných číslach až do 17. storočia, hoci Fibonacci používal pri riešení finančných problémov záporné čísla (Libier Abaci, 1202).
- Gottfried Wilhelm Leibniz bol prvý matematik, ktorý systematicky využíval záporné čísla.
Poznámka
Matematici v rôznych historických obdobiach považovali záporné čísla za absurdné (Diofantos), klamné (Descart) a fiktívne (Bombelli).
Matematici v rôznych historických obdobiach považovali záporné čísla za absurdné (Diofantos), klamné (Descart) a fiktívne (Bombelli).
Opačné čísla
Úloha:
Janko a Marienka mali za úlohu zistiť ako sa zmenila vonkajšia teplota na školskom dvore medzi 7 hodinou a 10 hodinou. Janko zistil, že teplota vzduchu v tomto časovom úseku stúpla o 5 stupňov, Marienka zistila, že teplota vzduchu o 10 hodine dosiahla len 2 stupne.
Na hodine matematiky mali žiaci 8. triedy vypočítať aká bola teplota vzduchu na školskom dvore ráno o 7 hodine.
Janko a Marienka mali za úlohu zistiť ako sa zmenila vonkajšia teplota na školskom dvore medzi 7 hodinou a 10 hodinou. Janko zistil, že teplota vzduchu v tomto časovom úseku stúpla o 5 stupňov, Marienka zistila, že teplota vzduchu o 10 hodine dosiahla len 2 stupne.
Na hodine matematiky mali žiaci 8. triedy vypočítať aká bola teplota vzduchu na školskom dvore ráno o 7 hodine.
Východisko pri zavádzaní celých resp. záporných čísel v školskej matematike je pojem opačného čísla.
Základná škola - Opačné čísla v našich učebniciach sú zavedené nasledovne:
- Šedivý, O. a kol.: Na číselnej osi sú zobrazené symetricky umiestnené body
 odkaz na učebnicu, str. 41, 54 Tu
Na interpretáciu záporných čísel sa používa okrem číselnej osi aj teplomer ako bežná praktická pomôcka pri meraní teploty (aj mínusovej).
odkaz na učebnicu, str. 41, 54 Tu
Na interpretáciu záporných čísel sa používa okrem číselnej osi aj teplomer ako bežná praktická pomôcka pri meraní teploty (aj mínusovej).
- Žabka, J.,Černek, P.:Vozenie hore - dole výťahom
 odkaz na učebnicu, str. 49 Tu
Na priblíženie pojmu záporného čísla sa používa výťah alebo nadmorská výška - dosť nereálne situácie pre záporné hodnoty.
odkaz na učebnicu, str. 49 Tu
Na priblíženie pojmu záporného čísla sa používa výťah alebo nadmorská výška - dosť nereálne situácie pre záporné hodnoty.
- Berovci: Na číselnej osi sú zobrazené symetricky umiestnené body
 odkaz na učebnicu, str. 7 Tu
Pri ukážke záporných čísel sa používajú príklady z oblasti financií a teplomer - naviac sa približuje reálnemu životu.
odkaz na učebnicu, str. 7 Tu
Pri ukážke záporných čísel sa používajú príklady z oblasti financií a teplomer - naviac sa približuje reálnemu životu.
- Situácie typu
 alebo
alebo 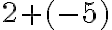 výhodne môžeme modelovať napríklad na financiách (pokúste sa interpretovať toto odčítanie pri platbe platobnou kartou).
výhodne môžeme modelovať napríklad na financiách (pokúste sa interpretovať toto odčítanie pri platbe platobnou kartou). - Zatiaľ nepoužívame názov záporné číslo.
- K pojmu záporného/opačného čísla si v rámci cvičenia vytvoríme dynamický applet, na ktorom budeme modelovať situácie o zmene teploty. Pozrite si ukážku teplomeru Tu a výťahu Tu. Na dynamickom teplomere vymodelujte situáciu, ktorá prezentuje riešenie rovnice
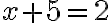 .
.
Modely záporných čísel
Modely
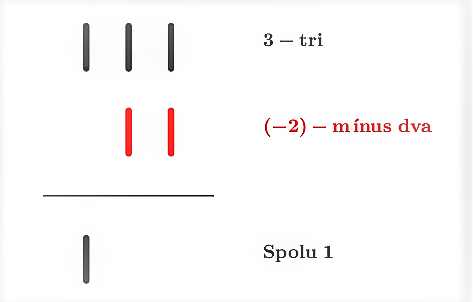
- Zaujímavý model pre upevňovanie pojmu záporné číslo sú čierne a červené paličky. Tento model vychádza z čínskeho spôsobu zápisu záporných čísel.
Tento model je vhodný aj pre žiakov základných škôl. Stačí im povedať pravidlo: Jedna čierna a jedna červená palička sa vyruší.
Teda rovnaký počet čiernych a červených paličiek dáva nulu. Potom napríklad rovnosť
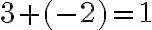
môžeme reprezentovať ako obrázok. - Model profesora Milana Hejného „Tajná chodba“ používa pravidlo:
- Výstup o jeden schod predstavuje prirodzené číslo 1
- Zostup o jeden schod predstavuje záporné číslo (-1)
- Potom matematickú úlohu na sčítanie v obore celých čísel môžeme prezentovať ako prechádzku po chodbe, v ktorej sa nachádzajú viaceré schodištia v smere nahor ako aj nadol.
Číselná os
Pravdepodobne najprirodzenejším a najpraktickejším modelom pre zobrazovanie celých čísel zrejme ostane číselná os.
Nech je daná priamka a nej body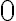 a
a 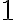 , pričom
, pričom 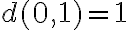 .
.
Applet si môžete stuahnuť Tu
Celému číslu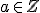 potom priradíme bod
potom priradíme bod 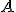 na osi
na osi  podľa pravidiel:
podľa pravidiel:
Pravdepodobne najprirodzenejším a najpraktickejším modelom pre zobrazovanie celých čísel zrejme ostane číselná os.
Nech je daná priamka a nej body
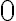 a
a 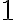 , pričom
, pričom 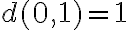 .
.
Applet si môžete stuahnuť Tu
Celému číslu
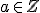 potom priradíme bod
potom priradíme bod 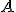 na osi
na osi  podľa pravidiel:
podľa pravidiel:
Operácie s celými číslami
Sčitovanie a odčitovanie
Sčitovanie a odčitovanie celých čísel sa v dostupných učebniciach matematiky zavádza postupne ako súčet:
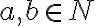 .
.
-
(uvádzame postup z učebnice Matematika od prof. Šedivého a kol.)
- dvoch kladných čísel
- dvoch záporných čísel
- kladného a záporného
- dvoch navzájom opačných čísel
- zdôrazňuje sa tvrdenie: "Odčítať záporné číslo znamená pričítať číslo opačné."
- samostatná časť je venovaná počítaniu s nulou.
V závere tohto tematického celku je tento postup názorne zhrnutý pri prezentovaní riešenia príkladu:

V učebnici Žabka - Černek je odčítanie dvoch celých čísel prezentované pomocou pričítania opačného čísla:

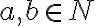 .
.
Poznámky.
- Pre žiakov 8. ročníka sčítanie a odčítanie nepredstavuje náročné učivo, keďže sa s v bežnom živote stretávajú aj s úlohami pre odčítanie, v ktorých je výsledok záporné číslo. Sú to prevažne úlohy o teplote a financiách.
- Ak ich chceme žiakov naučiť "sčitovať" dve celé čísla musíme s nimi preriešiť dostatočné množstvo príkladov s konkrétnymi číslami, ktoré korešpondujú so situáciami v bežnom živote.
- Pre sčítanie a odčítanie celých čísel môžete využiť celú škálu modelov vytvorených v prostredí GeoGebra. Ako príklady uvádzame modely
- "Číselný rad na sčítanie a odčítanie" od autora Bo Kristensen
- "Odčítanie dvoch celých čísel" od autora Kwanchau
- "Číselný rad na sčítanie a odčítanie" od autora Bo Kristensen
- Pri riešení úloh sa používajú aj formulácie typu: "Ak absolútna hodnota čísla je väčšia ..., tak odčítame ...", ktoré sú pre žiakov málo vypovedajúce. Preto uprednostňujeme formulácie: "Ktorá z "cifier"
 predstavuje väčšie prirodzené číslo".
predstavuje väčšie prirodzené číslo".
Násobenie a delenie
Medzi základné operácie v aritmetike celých čísel
patrí násobenie a delenie celých čísel. V oboch porovnávaných učebniciach (Šedivý, Žabka) sa problematika násobenia celých opiera o násobenie typu
kladné celé číslo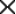 záporné celé číslo
záporné celé číslo
kladné celé číslo
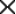 záporné celé číslo
záporné celé číslo
Šedivý:

Žabka


Žabka

Na precvičovanie opäť môžeme vybrať celý rad appletov, ktoré intepretujú operácie násobenia a delenia
- "Násobenie a delenie celých čísel" od Kwanchau:
- "Násobenie a delenie celých čísel" od Mr. Reilly:
- "Násobenie a delenie celých čísel" od Silverman:
Cvičenie.
Pripravte si prezentáciu o násobení a delení celých čísel podľa učebnice od autorov Bero a Berová.
Pripravte si prezentáciu o násobení a delení celých čísel podľa učebnice od autorov Bero a Berová.
Racionálne čísla
Príklad
Mamka išla nakúpiť zeleninu. Kúpila 6 balení zemiakov a 3kg uhoriek. Spolu tak mala v taške 6kg zeleniny. Na hodine matematiky mali žiaci 8. triedy vypočítať koľko kg váži 1 balenie zemiakov.
Mamka išla nakúpiť zeleninu. Kúpila 6 balení zemiakov a 3kg uhoriek. Spolu tak mala v taške 6kg zeleniny. Na hodine matematiky mali žiaci 8. triedy vypočítať koľko kg váži 1 balenie zemiakov.
Pri riešení dospeli k algebrickej rovnici 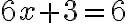 , ktorej koeficienty
, ktorej koeficienty
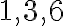 sú celé čísla. Takúto rovnicu však nedokážu vyriešiť v obore celých čísel. Prečo?
sú celé čísla. Takúto rovnicu však nedokážu vyriešiť v obore celých čísel. Prečo?
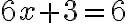 , ktorej koeficienty
, ktorej koeficienty
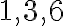 sú celé čísla. Takúto rovnicu však nedokážu vyriešiť v obore celých čísel. Prečo?
sú celé čísla. Takúto rovnicu však nedokážu vyriešiť v obore celých čísel. Prečo?Stačí pripočítať k obidvom stranám rovnice číslo
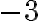 a dostaneme rovnicu
a dostaneme rovnicu 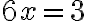 , ktorej riešením nemôže byť celé číslo.
, ktorej riešením nemôže byť celé číslo.
Na ľavej strane rovnice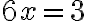 máme párne číslo
máme párne číslo 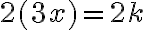 , ale na pravej strane nepárne číslo
, ale na pravej strane nepárne číslo 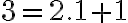 . To nie je možné!
. To nie je možné!
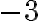 a dostaneme rovnicu
a dostaneme rovnicu 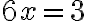 , ktorej riešením nemôže byť celé číslo.
, ktorej riešením nemôže byť celé číslo. Na ľavej strane rovnice
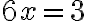 máme párne číslo
máme párne číslo 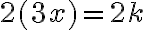 , ale na pravej strane nepárne číslo
, ale na pravej strane nepárne číslo 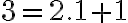 . To nie je možné!
. To nie je možné!
Východisko pri zavádzaní racionálnych čísel v školskej matematike je pojem zlomku.
-
Na chvíľu predpokladajme, že existuje celé číslo, ktoré je riešením danej rovnice
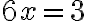 .
. - Z vlastností operácie násobenia vieme, že také číslo
 je rovné podielu
je rovné podielu 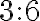 . Teda muselo by platiť:
. Teda muselo by platiť: 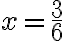 .
. - Zároveň zo základnej školy vieme, že rovnicu
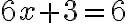 môžeme upraviť na tvar
môžeme upraviť na tvar 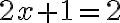 .
. - Riešením tejto rovnice je aj číslo
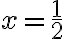 , ktoré tiež nie je celé.
, ktoré tiež nie je celé.
-
Zistili sme, že rovnica
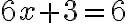 sú má dve riešenia: „podiely“
sú má dve riešenia: „podiely“ 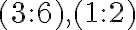 resp. zlomky
resp. zlomky 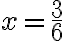 ,
, 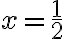 .
.
Reálne čísla
Reálne čísla sú čísla racionálne a čísla iracionálne, pričom iracionálne čísla sú čísla, ktoré sa nedajú vyjadriť v tvare zlomku 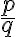 .
.
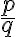 .
.
Termín reálne číslo zaviedol René Descartes (1637) ako spoločný názov pre racionálne a iracionálne čísla
- Viac ako dve tisíc rokov boli známe typy iracionálnych čísel ako odmocniny niektorých prirodzených čísel
![\sqrt {2}, \sqrt[3]{2} \sqrt {2}, \sqrt[3]{2}](https://lms.umb.sk/filter/tex/pix.php/8eab57a71ea77676be24a2790112fe76.png) ...
... - Euler (1737) dokázal, že číslo
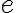 je iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
je iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo 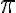 je iracionálne
je iracionálne - Charles Hermit (1873) ukázal, že číslo
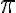 je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami
je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami
Pytagorova škola
Matematik Pytagorovej školy Hippasus (5. stor. pred n. l.) ukázal, že uhlopriečka štvorca s jednotkovou stranou nemôže byť vyjadrená racionálnym číslom1)
Hippasus pravdepodobne dospel k záveru, že
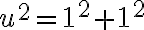 a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi
a po úprave dostal kvadratickú rovnicu s celočíselnými koeficientmi 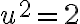 .
.
S využitím vlastností deliteľnosti ukážeme, že táto rovnica nemá v obore racionálnych čísel
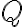 riešenie.
riešenie.
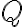 riešenie.
riešenie.
Dokážeme to nepriamo.
Nech existuje racionálne číslo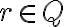 , ktoré je riešením rovnice
, ktoré je riešením rovnice 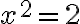 . Potom zrejme
. Potom zrejme
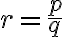 , pričom celé čísla
, pričom celé čísla
 sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
 je rovný
je rovný
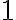 .
.
Po dosadení do rovnice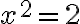 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť
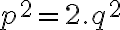 . Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
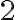 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
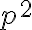 je párne, preto musí byť aj číslo
je párne, preto musí byť aj číslo
 párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare
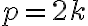 . Po dosadení do rovnosti
. Po dosadení do rovnosti
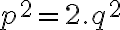 dostávame
dostávame
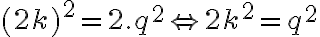 .
.
Analogickou úvahou zistíme, že číslo je párne. Keďže aj číslo
je párne. Keďže aj číslo
 je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel
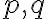 je väčší alebo rovný číslu
je väčší alebo rovný číslu
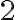 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo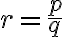 , kde
, kde
 sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
Nech existuje racionálne číslo
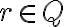 , ktoré je riešením rovnice
, ktoré je riešením rovnice 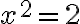 . Potom zrejme
. Potom zrejme
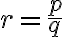 , pričom celé čísla
, pričom celé čísla
 sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
sú nesúdeliteľné. Najväčší spoločný deliteľ čísel
 je rovný
je rovný
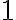 .
.
Po dosadení do rovnice
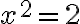 a po ekvivalentných úpravách dostaneme rovnosť
a po ekvivalentných úpravách dostaneme rovnosť
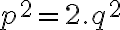 . Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
. Na pravej strane rovnosti je určite číslo párne. Z vlastností deliteľnosti celých čísel vyplýva, že číslo
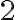 delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
delí číslo na pravej strane rovnosti a zároveň musí deliť aj číslo na ľavej strane rovnosti. Využijeme skutočnosť, že druhá mocnina párneho čísla je opäť párne číslo a druhá
mocnina nepárneho čísla je nepárne číslo. Teda číslo
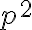 je párne, preto musí byť aj číslo
je párne, preto musí byť aj číslo
 párne. (Dokážte to). To znamená, že je v tvare
párne. (Dokážte to). To znamená, že je v tvare
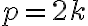 . Po dosadení do rovnosti
. Po dosadení do rovnosti
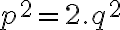 dostávame
dostávame
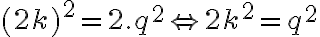 .
.
Analogickou úvahou zistíme, že číslo
 je párne. Keďže aj číslo
je párne. Keďže aj číslo
 je párne, tak najväčší spoločný deliteľ čísel
je párne, tak najväčší spoločný deliteľ čísel
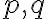 je väčší alebo rovný číslu
je väčší alebo rovný číslu
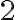 .
.
To je spor s našim predpokladom, že riešením je racionálne číslo
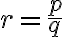 , kde
, kde
 sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
sú nesúdeliteľné celé čísla. Pozrite si zápis dôkazu v GeoGebre Tu.
___________________________________________________________________________________________
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
1) Podľa povesti bol Hippasus zvrhnutý z lode do mora a utopený, aby tento objav zostal utajený.
Seminárne zadanie
- V GeoGebre vytvorte applet pre model "Teplomer". Postup konštrukcie si otvorte Tu.
- Vytvorte aspoň jednu prezentáciu s niektorou s tém:
- Diofantické rovnice
- Fibonacciho čísla
- Trojuholníkové čísla
Cvičenie
- Nech
 , kde
, kde 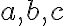 sú prirodzené čísla. Potom existujú také celé čísla
sú prirodzené čísla. Potom existujú také celé čísla 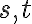 , že
, že 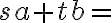 nsd
nsd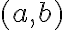 .
Použite matematickú indukciu a Euklidov algoritmus. Larson, 3.1.2.
.
Použite matematickú indukciu a Euklidov algoritmus. Larson, 3.1.2. - Rovnica
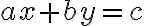 , kde
, kde 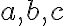 sú celé čísla, má celočíselné riešenie práve vtedy, keď
sú celé čísla, má celočíselné riešenie práve vtedy, keď 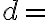 nsd
nsd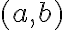 delí
delí  .
Ak navyše
.
Ak navyše 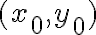 je nejaké celočíselné riešenie, tak pre každé celé číslo
je nejaké celočíselné riešenie, tak pre každé celé číslo  aj čísla
aj čísla 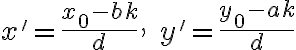 sú riešením a
všetky celočíselné riešenia majú tento tvar. Larson, 3.1.4.
sú riešením a
všetky celočíselné riešenia majú tento tvar. Larson, 3.1.4. - Navrhnite postup ako nabrať jeden liter vody ak máme k dispozícii len 9 a 16 litrovú nádobu.
- Dokážte, že pre každé prirodzené číslo
 je zlomok
je zlomok 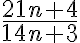 v základnom tvare. Larson, 3.1.5.
v základnom tvare. Larson, 3.1.5. - Dokážte, že pre každé dve za sebou idúce Fibonacciho čísla
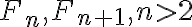 sú navzájom nesúdeliteľné v základnom tvare. Larson, 3.1.10.
sú navzájom nesúdeliteľné v základnom tvare. Larson, 3.1.10.