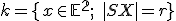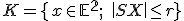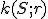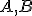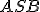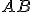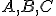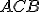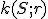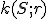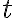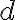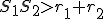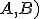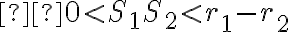Geometria kružnice
Kružnica, kruh
Definícia.
Množina všetkých bodov v rovine, ktoré majú od pevného bodu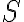 vzdialenosť rovnú kladnému reálnemu číslu
vzdialenosť rovnú kladnému reálnemu číslu 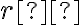 sa nazýva kružnica so stredom
sa nazýva kružnica so stredom  a polomerom
a polomerom  . Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu  vzdialenosť menšiu alebo rovnú číslu
vzdialenosť menšiu alebo rovnú číslu  sa nazýva kruh so stredom
sa nazýva kruh so stredom  a polomerom
a polomerom  . Symbolicky
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
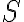 vzdialenosť rovnú kladnému reálnemu číslu
vzdialenosť rovnú kladnému reálnemu číslu 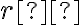 sa nazýva kružnica so stredom
sa nazýva kružnica so stredom  a polomerom
a polomerom  . Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu  vzdialenosť menšiu alebo rovnú číslu
vzdialenosť menšiu alebo rovnú číslu  sa nazýva kruh so stredom
sa nazýva kruh so stredom  a polomerom
a polomerom  . Symbolicky
. Symbolicky
Bod
 nazývame stred kružnice resp. stred kruhu a číslo
nazývame stred kružnice resp. stred kruhu a číslo 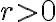 polomer kružnice resp. kruhu.
polomer kružnice resp. kruhu.
Ľubovoľné dva body kružnice delia túto kružnicu na dve časti, ktoré nazývame oblúky kružnice alebo kružnicové oblúky.
Dva polomery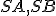 rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
Tetiva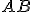 rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
 nazývame stred kružnice resp. stred kruhu a číslo
nazývame stred kružnice resp. stred kruhu a číslo 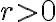 polomer kružnice resp. kruhu.
polomer kružnice resp. kruhu.
Ľubovoľné dva body kružnice delia túto kružnicu na dve časti, ktoré nazývame oblúky kružnice alebo kružnicové oblúky.
Dva polomery
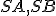 rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
Tetiva
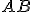 rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
Definícia.
V geometrii skúmame vlastnosti geometrických útvarov v dvoch základných kategóriách, ktoré zahŕňajú:
- polohové vlastnosti,
- metrické vlastnosti.
- vzájomnú polohu priamky a kružnice,
- vzájomnú polohu dvoch kružníc.
- vzťah medzi veľkosťou stredového uhla a prislúchajúcich obvodových uhloch v kružnici,
- mocnosť bodu ku kružnici.
Je daná kružnica 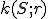 a priamka
a priamka  . Nech
. Nech 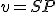 je vzdialenosť priamky od stredu kružnice
je vzdialenosť priamky od stredu kružnice  .
.
Môžu nastať len tri prípady: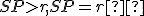 alebo
alebo 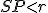 .
Aktivujte zaškrtávacie políčko v applete.
.
Aktivujte zaškrtávacie políčko v applete.
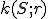 a priamka
a priamka  . Nech
. Nech 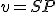 je vzdialenosť priamky od stredu kružnice
je vzdialenosť priamky od stredu kružnice  .
.
Môžu nastať len tri prípady:
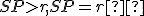 alebo
alebo 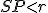 .
Aktivujte zaškrtávacie políčko v applete.
.
Aktivujte zaškrtávacie políčko v applete.
-
Ak má priamka
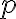 od stredu
od stredu 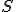 kružnice
kružnice 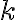 vzdialenosť
vzdialenosť 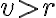 , tak priamka
, tak priamka  kružnicu
kružnicu 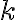 nepretína.
nepretína. -
Ak priamka má od stredu kružnice vzdialenosť rovnú polomeru
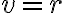 , tak má priamka s kružnicou jediný spoločný bod
, tak má priamka s kružnicou jediný spoločný bod 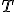 .
. - Priamka, ktorá má s kružnicou jediný spoločný bod, sa nazýva dotyčnica kružnice.
- Spoločný bod priamky a kružnice je bod dotyku.
- Dotyčnica je vždy kolmá na polomer kružnice
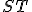 .
.
-
Ak má priamka od stredu kružnice vzdialenosť
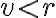 , tak má priamka a kružnica dva rôzne spoločné body.
, tak má priamka a kružnica dva rôzne spoločné body. - Priamka, ktorá má s kružnicou dva rôzne spoločné body, sa nazýva sečnica kružnice.
- Spoločné body priamky a kružnice sú ich priesečníky.
Definícia.
Dané dve kružnice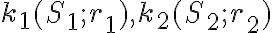 s rôznymi stredmi. Priamka (resp. úsečka)
s rôznymi stredmi. Priamka (resp. úsečka) 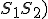 )
sa nazýva stredná týchto dvoch kružníc.
)
sa nazýva stredná týchto dvoch kružníc.
Dané dve kružnice
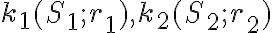 s rôznymi stredmi. Priamka (resp. úsečka)
s rôznymi stredmi. Priamka (resp. úsečka) 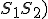 )
sa nazýva stredná týchto dvoch kružníc.
)
sa nazýva stredná týchto dvoch kružníc.