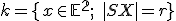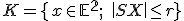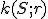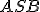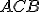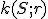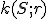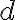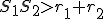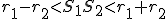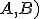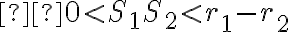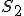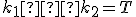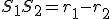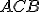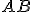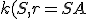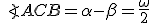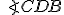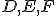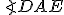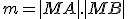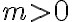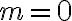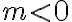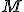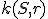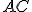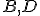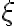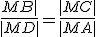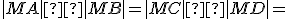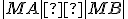Geometria kružnice
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Geometria kružnice |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:41 |
Kružnica, kruh
Definícia.
Množina všetkých bodov v rovine, ktoré majú od pevného bodu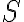 vzdialenosť rovnú kladnému reálnemu číslu
vzdialenosť rovnú kladnému reálnemu číslu 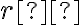 sa nazýva kružnica so stredom
sa nazýva kružnica so stredom  a polomerom
a polomerom  . Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu  vzdialenosť menšiu alebo rovnú číslu
vzdialenosť menšiu alebo rovnú číslu  sa nazýva kruh so stredom
sa nazýva kruh so stredom  a polomerom
a polomerom  . Symbolicky
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
 vzdialenosť rovnú kladnému reálnemu číslu
vzdialenosť rovnú kladnému reálnemu číslu 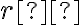 sa nazýva kružnica so stredom
sa nazýva kružnica so stredom  a polomerom
a polomerom  . Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu
. Symbolicky
Množina všetkých bodov v rovine, ktoré majú od pevného bodu  vzdialenosť menšiu alebo rovnú číslu
vzdialenosť menšiu alebo rovnú číslu  sa nazýva kruh so stredom
sa nazýva kruh so stredom  a polomerom
a polomerom  . Symbolicky
. Symbolicky
Bod
 nazývame stred kružnice resp. stred kruhu a číslo
nazývame stred kružnice resp. stred kruhu a číslo 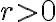 polomer kružnice resp. kruhu.
polomer kružnice resp. kruhu.
Ľubovoľné dva body kružnice delia túto kružnicu na dve časti, ktoré nazývame oblúky kružnice alebo kružnicové oblúky.
Dva polomery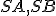 rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
Tetiva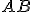 rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
 nazývame stred kružnice resp. stred kruhu a číslo
nazývame stred kružnice resp. stred kruhu a číslo 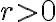 polomer kružnice resp. kruhu.
polomer kružnice resp. kruhu.
Ľubovoľné dva body kružnice delia túto kružnicu na dve časti, ktoré nazývame oblúky kružnice alebo kružnicové oblúky.
Dva polomery
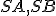 rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
rozdelia kruh na dve časti, ktoré nazývame kruhové výseky.
Tetiva
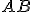 rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
rozdelí kruh na dve časti, ktoré nazývame kruhové odseky.
Definícia.
V geometrii skúmame vlastnosti geometrických útvarov v dvoch základných kategóriách, ktoré zahŕňajú:
- polohové vlastnosti,
- metrické vlastnosti.
- vzájomnú polohu priamky a kružnice,
- vzájomnú polohu dvoch kružníc.
- vzťah medzi veľkosťou stredového uhla a prislúchajúcich obvodových uhloch v kružnici,
- mocnosť bodu ku kružnici.
Je daná kružnica 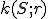 a priamka
a priamka  . Nech
. Nech 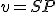 je vzdialenosť priamky od stredu kružnice
je vzdialenosť priamky od stredu kružnice  .
.
Môžu nastať len tri prípady: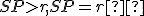 alebo
alebo 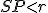 .
Aktivujte zaškrtávacie políčko v applete.
.
Aktivujte zaškrtávacie políčko v applete.
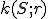 a priamka
a priamka  . Nech
. Nech 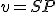 je vzdialenosť priamky od stredu kružnice
je vzdialenosť priamky od stredu kružnice  .
.
Môžu nastať len tri prípady:
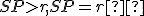 alebo
alebo 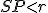 .
Aktivujte zaškrtávacie políčko v applete.
.
Aktivujte zaškrtávacie políčko v applete.
-
Ak má priamka
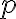 od stredu
od stredu 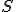 kružnice
kružnice 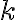 vzdialenosť
vzdialenosť 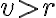 , tak priamka
, tak priamka  kružnicu
kružnicu 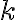 nepretína.
nepretína. -
Ak priamka má od stredu kružnice vzdialenosť rovnú polomeru
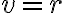 , tak má priamka s kružnicou jediný spoločný bod
, tak má priamka s kružnicou jediný spoločný bod 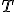 .
. - Priamka, ktorá má s kružnicou jediný spoločný bod, sa nazýva dotyčnica kružnice.
- Spoločný bod priamky a kružnice je bod dotyku.
- Dotyčnica je vždy kolmá na polomer kružnice
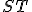 .
.
-
Ak má priamka od stredu kružnice vzdialenosť
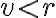 , tak má priamka a kružnica dva rôzne spoločné body.
, tak má priamka a kružnica dva rôzne spoločné body. - Priamka, ktorá má s kružnicou dva rôzne spoločné body, sa nazýva sečnica kružnice.
- Spoločné body priamky a kružnice sú ich priesečníky.
Definícia.
Dané dve kružnice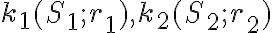 s rôznymi stredmi. Priamka (resp. úsečka)
s rôznymi stredmi. Priamka (resp. úsečka) 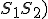 )
sa nazýva stredná týchto dvoch kružníc.
)
sa nazýva stredná týchto dvoch kružníc.
Dané dve kružnice
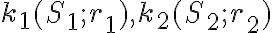 s rôznymi stredmi. Priamka (resp. úsečka)
s rôznymi stredmi. Priamka (resp. úsečka) 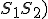 )
sa nazýva stredná týchto dvoch kružníc.
)
sa nazýva stredná týchto dvoch kružníc.
Veta o obvodových uholch
Veta (O obvodových uhloch).
Ľubovoľné dva obvodové uhly prislúchajúce k tomu istému oblúku kružnice majú rovnakú veľkosť.
Obvodový uhol je polovicou stredového uhla prislúchajúceho k tomu istému oblúku.
Ľubovoľné dva obvodové uhly prislúchajúce k tomu istému oblúku kružnice majú rovnakú veľkosť.
Obvodový uhol je polovicou stredového uhla prislúchajúceho k tomu istému oblúku.
-
Priložený applet je motivačný a môžete ho využiť pri skúmaní závislosti veľkosti obvodových uhlov
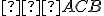 od polohy bodu
od polohy bodu  .
. -
Veľkosť obvodového uhla nezávisí od polohy bodu
 , rozhodujúce sú body
, rozhodujúce sú body 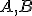 resp. uhol
resp. uhol 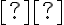 .
. - Konštrukcia oblúka, z ktorého vidieť úsečku pod daným uhlom. Otvorte si konštrukciu Tu.<\li>
- Ak body
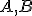 sú krajné body priemeru, tak rozdelia kružnicu na dve polkružnice: stredový uhol je priamy a obvodový uhol pravý.
sú krajné body priemeru, tak rozdelia kružnicu na dve polkružnice: stredový uhol je priamy a obvodový uhol pravý.
Dôkaz (vety o obvodových uhloch).
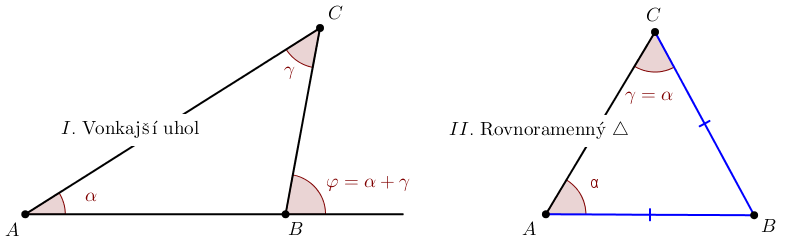
V dôkaze vety o obvodových uhloch sa využívajú dve základné vlastnosti trojuholníka.
Spojením týchto dvoch tvrdení dostaneme:
V dôkaze vety o obvodových uhloch sa využívajú dve základné vlastnosti trojuholníka.
- "Vonkajší uhol trojuholníka sa rovná súčtu vnútorných uhlov pri zvyšných vrcholoch."
- "V rovnoramennom trojuholníku sa uhly pri základni navzájom rovnajú" (Kniha 1, Tvrdenie V).
Spojením týchto dvoch tvrdení dostaneme:
Dôsledok.
Prípad 1 (Veta o obvodových uhloch).
Nech je vnútorný bod uhla
je vnútorný bod uhla 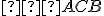 . Potom obvodový uhol
. Potom obvodový uhol 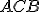 je polovicou stredového
uhla
je polovicou stredového
uhla 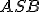 .
.
Nech
 je vnútorný bod uhla
je vnútorný bod uhla 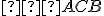 . Potom obvodový uhol
. Potom obvodový uhol 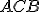 je polovicou stredového
uhla
je polovicou stredového
uhla 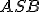 .
.
Prípad 2 (Veta o obvodových uhloch).
Nech leží na ramene uhla
leží na ramene uhla 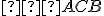 Potom obvodový uhol
Potom obvodový uhol 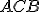 je tiež polovicou stredového uhla
je tiež polovicou stredového uhla 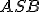 .
.
Nech
 leží na ramene uhla
leží na ramene uhla 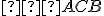 Potom obvodový uhol
Potom obvodový uhol 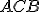 je tiež polovicou stredového uhla
je tiež polovicou stredového uhla 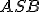 .
.
Posuňte bod C proti smeru hodinových ručičiek do krajnej polohy vľavo tak, aby body 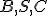 ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
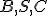 ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
ležali na jednej priamke (boli kolineárne). Potom dôkaz pre prípad 2 bude analogický ako v prípade 1. Situácia sa transformuje len na jeden trojuholník.
Prípad 3 (Veta o obvodových uhloch).
Nech S je vonkajší bod uhla ∡ACB. Potom obvodový uhol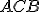 je polovicou stredového uhla
je polovicou stredového uhla 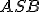 .
.
Nech S je vonkajší bod uhla ∡ACB. Potom obvodový uhol
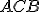 je polovicou stredového uhla
je polovicou stredového uhla 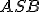 .
.
Zrejme platí 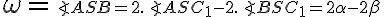 . Pozrime sa na rozdiel uhlov pri vrchole
. Pozrime sa na rozdiel uhlov pri vrchole 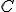 .
Zistíme, že
.
Zistíme, že 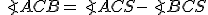 . Keďže trojuholníky
. Keďže trojuholníky 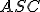 ,
, 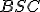 sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod
sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod 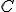 môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
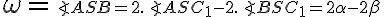 . Pozrime sa na rozdiel uhlov pri vrchole
. Pozrime sa na rozdiel uhlov pri vrchole 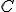 .
Zistíme, že
.
Zistíme, že 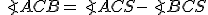 . Keďže trojuholníky
. Keďže trojuholníky 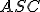 ,
, 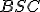 sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod
sú rovnoramenné, tak platí
Pozrite si konštrukčný dôkaz od Martina Vinklera, ktorý je dostupný Tu. Pre bod 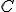 môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
môžu nastať len tieto tri prípady, preto je dôkaz vety o obvodových uhloch ukončený.
Príklad.
Určte veľkosti vnútorných (obvodových) uhlov trojuholníka s vrcholmi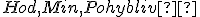 na hodinovom ciferníku znázorneného na obrázku "Ciferník". Zmeňte nastavenie hodín na 8:00 a bod Pohyblivý na pozíciu 15:00, určte veľkosti vnútorných uhlov pre takéto nastavenie. Po otvorení appletu, čas môžete meniť použitím posuvníkov.
na hodinovom ciferníku znázorneného na obrázku "Ciferník". Zmeňte nastavenie hodín na 8:00 a bod Pohyblivý na pozíciu 15:00, určte veľkosti vnútorných uhlov pre takéto nastavenie. Po otvorení appletu, čas môžete meniť použitím posuvníkov.
Určte veľkosti vnútorných (obvodových) uhlov trojuholníka s vrcholmi
 na hodinovom ciferníku znázorneného na obrázku "Ciferník". Zmeňte nastavenie hodín na 8:00 a bod Pohyblivý na pozíciu 15:00, určte veľkosti vnútorných uhlov pre takéto nastavenie. Po otvorení appletu, čas môžete meniť použitím posuvníkov.
na hodinovom ciferníku znázorneného na obrázku "Ciferník". Zmeňte nastavenie hodín na 8:00 a bod Pohyblivý na pozíciu 15:00, určte veľkosti vnútorných uhlov pre takéto nastavenie. Po otvorení appletu, čas môžete meniť použitím posuvníkov.
V planimetrii sa pomerne často vyskytujú úlohy, v ktorých sa hľadá množina  bodov s danou vlastnosťou
bodov s danou vlastnosťou 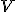 .
Symolicky to môžeme zapísať takto
.
Symolicky to môžeme zapísať takto 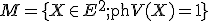 . Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
. Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
 bodov s danou vlastnosťou
bodov s danou vlastnosťou 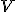 .
Symolicky to môžeme zapísať takto
.
Symolicky to môžeme zapísať takto 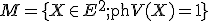 . Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
. Takéto množiny sa tiež označujú ako "Geometrické miesta bodov (GMB)". Riešenie takýchto úloh sa
skladá z troch častí:
Ukážka
♥ Je daná kružnica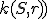 a na nej dva body
a na nej dva body 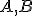 .
Pre každý priemer (\small XY\) kružnice
.
Pre každý priemer (\small XY\) kružnice  zostrojíme (ak existuje) priesečník priamok
zostrojíme (ak existuje) priesečník priamok 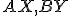 .
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že
.
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že 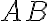 nie je priemer kružnice. (Larson 8.1.2.).
nie je priemer kružnice. (Larson 8.1.2.).
V tomto prípade budeme pri experimentovaní postupovať takto: je kružnicový
oblúk
je kružnicový
oblúk 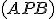 . Na overenie platnosti výroku "
. Na overenie platnosti výroku "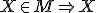 má vlastnosť
má vlastnosť 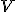 " teraz stačí ukázať, že výroková formula
" teraz stačí ukázať, že výroková formula
![[(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.) [(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.)](https://lms.umb.sk/filter/tex/pix.php/1d2466a43806dc0ae93b0078ee6c0d9a.png) je tautológia.
To je však zrejmé. Keďže aj opačný postup
je tautológia.
To je však zrejmé. Keďže aj opačný postup ![[(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1. [(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1.](https://lms.umb.sk/filter/tex/pix.php/1b9ba53c25e2235ca080665d0afdfcae.png) je tautológia, tak aj časť C je pravdivý výrok.
je tautológia, tak aj časť C je pravdivý výrok.
♥ Je daná kružnica
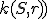 a na nej dva body
a na nej dva body 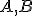 .
Pre každý priemer (\small XY\) kružnice
.
Pre každý priemer (\small XY\) kružnice  zostrojíme (ak existuje) priesečník priamok
zostrojíme (ak existuje) priesečník priamok 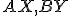 .
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že
.
Určte množinu všetkých takých priesečníkov. Budeme predpokladať, že 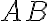 nie je priemer kružnice. (Larson 8.1.2.).
nie je priemer kružnice. (Larson 8.1.2.).
V tomto prípade budeme pri experimentovaní postupovať takto:
- Thalesova veta hovorí, že trojuholníky
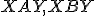 sú pravouhlé s pravým uhlom pri vrcholoch
sú pravouhlé s pravým uhlom pri vrcholoch 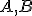 .
. - Obvodové uhly
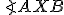 a
a 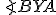 majú rovnakú veľkosť
majú rovnakú veľkosť  .
. - Označme si
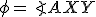 a
a 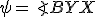 .
. - Súčet uhlov v trojuholníku je 180°, preto
bude
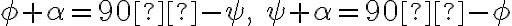 .
. - Odtiaľ dostávame, že súčet uhlov
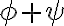 je konštantný pre ľubovoľný priemer
je konštantný pre ľubovoľný priemer 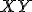 a dva pevné body
a dva pevné body 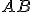 .
. - Preto aj vrcholové uhly
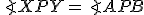 majú konštantnú veľkosť. To znamená, že body
majú konštantnú veľkosť. To znamená, že body  ležia na kružnicovom oblúku
ležia na kružnicovom oblúku
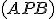 .
. - K nájdeniu oblúka stačí zvoliť jeden priemer
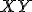 a jeden odpovedajúci priesečník
a jeden odpovedajúci priesečník 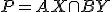 .
.
 je kružnicový
oblúk
je kružnicový
oblúk 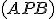 . Na overenie platnosti výroku "
. Na overenie platnosti výroku "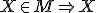 má vlastnosť
má vlastnosť 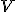 " teraz stačí ukázať, že výroková formula
" teraz stačí ukázať, že výroková formula
![[(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.) [(1. \wedge 2.) \Rightarrow 4] \Rightarrow (5. \wedge 6.)](https://lms.umb.sk/filter/tex/pix.php/1d2466a43806dc0ae93b0078ee6c0d9a.png) je tautológia.
To je však zrejmé. Keďže aj opačný postup
je tautológia.
To je však zrejmé. Keďže aj opačný postup ![[(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1. [(5. \wedge 6.) \Rightarrow 4.] \Rightarrow 1.](https://lms.umb.sk/filter/tex/pix.php/1b9ba53c25e2235ca080665d0afdfcae.png) je tautológia, tak aj časť C je pravdivý výrok.
je tautológia, tak aj časť C je pravdivý výrok.
Poznámky.
- Pri určovaní GMB je mnohokrát najťažší krok A.
- Program GeoGebra tento krok zjednoduší tým, že pomocou nástroja "Množina bodov" (nachádza sa v sekcii nástrojov "Kolmica") vykreslí hľadanú
množinu
 .
. - Potom je však nutné realizovať kroky B a C.
- Pozrite si aplikovanie tohto nástroja v kurze Didaktika matematiky v knihe Množiny bodov. Dostupné Tu.
Cvičenie.
Mocnosť bodu ku kružnici
Je daná kružnica 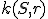 so stredom
so stredom  a polomerom
a polomerom 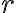 . Bod
. Bod  leží zvonka kružnice. Nech
leží zvonka kružnice. Nech 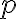 je sečnica
kružnice
je sečnica
kružnice 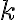 vedená bodom
vedená bodom  a
a  sú priesečníky sečnice s kružnicou
sú priesečníky sečnice s kružnicou 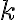 .
.
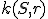 so stredom
so stredom  a polomerom
a polomerom 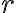 . Bod
. Bod  leží zvonka kružnice. Nech
leží zvonka kružnice. Nech 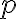 je sečnica
kružnice
je sečnica
kružnice 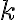 vedená bodom
vedená bodom  a
a  sú priesečníky sečnice s kružnicou
sú priesečníky sečnice s kružnicou 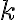 .
.
Skúmajme súčin 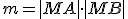 . Po otvorení motivačného appletu a experimentovaním s polohou bodu
. Po otvorení motivačného appletu a experimentovaním s polohou bodu  , môžeme vysloviť hypotézu:
, môžeme vysloviť hypotézu:
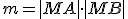 . Po otvorení motivačného appletu a experimentovaním s polohou bodu
. Po otvorení motivačného appletu a experimentovaním s polohou bodu  , môžeme vysloviť hypotézu:
, môžeme vysloviť hypotézu:
Otvorte si motivačný applet Tu.
Otázky.
Je súčin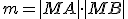 nezávislý od polohy sečnice
nezávislý od polohy sečnice 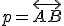 ? Inými slovami je konštantný pre ľubovoľnú polohu bodov
? Inými slovami je konštantný pre ľubovoľnú polohu bodov  ?
?
Môžeme definovať súčin aj pre prípad, ak bod leží vo vnútri kružnice
leží vo vnútri kružnice 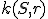 ? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
Je súčin
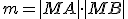 nezávislý od polohy sečnice
nezávislý od polohy sečnice 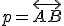 ? Inými slovami je konštantný pre ľubovoľnú polohu bodov
? Inými slovami je konštantný pre ľubovoľnú polohu bodov  ?
?
Môžeme definovať súčin aj pre prípad, ak bod
 leží vo vnútri kružnice
leží vo vnútri kružnice 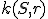 ? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
? Odpovede nájdeme vo forme dôkazov viet o mocnosti.
Definícia (Mocnosť bodu ku kružnici).
Ľubovoľnému bodu roviny možno priradiť reálne číslo
roviny možno priradiť reálne číslo 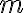 , pre ktorého absolútnu hodnotu platí
, pre ktorého absolútnu hodnotu platí 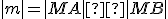 , pričom
, pričom
Ľubovoľnému bodu
 roviny možno priradiť reálne číslo
roviny možno priradiť reálne číslo 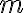 , pre ktorého absolútnu hodnotu platí
, pre ktorého absolútnu hodnotu platí 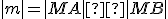 , pričom
, pričom
Dôkaz.
Dokázať tento dôsledok je veľmi jednoduché. Stačí zvoliť sečnicu 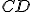 tak, aby prechádzala stredom kružnice. V takom prípade bude
tak, aby prechádzala stredom kružnice. V takom prípade bude
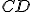 tak, aby prechádzala stredom kružnice. V takom prípade bude
tak, aby prechádzala stredom kružnice. V takom prípade bude
Poznámka.
V prípade, keď bod leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky
leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky 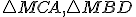 sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo
sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo 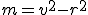 záporné. Pozrite si ilustračný obrázok.
záporné. Pozrite si ilustračný obrázok.
V prípade, keď bod
 leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky
leží vo vnútri kružnice tvrdenie vety 1 a tvrdenie dôsledku ostáva v platnosti. Trojuholníky 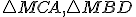 sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo
sú podobné. Naviac v súlade s definíciou mocnosti bodu ku kružnici, bude v prípade bodu ležiaceho vo vnútri kružnice, číslo 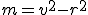 záporné. Pozrite si ilustračný obrázok.
záporné. Pozrite si ilustračný obrázok.
Nasledujúca veta platí len v prípade, že bod
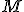 je mimo kružnice
je mimo kružnice  . Mocnosť bodu
. Mocnosť bodu 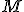 v tomto prípade môžeme vyjadriť
pomocou veľkosti úsečky
v tomto prípade môžeme vyjadriť
pomocou veľkosti úsečky 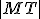 , kde
, kde 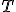 je dotykový bod dotyčnice ku kružnici, ktorá prechádza bodom
je dotykový bod dotyčnice ku kružnici, ktorá prechádza bodom 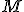 .
.
Veta 2.
Pre mocnosť bodu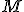 , ktorý leží zvonka kružnice
, ktorý leží zvonka kružnice 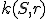 , platí rovnosť
, platí rovnosť 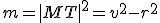 . Bod
. Bod 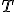 je dotykový bod dotyčnice, ktorá prechádza bodom
je dotykový bod dotyčnice, ktorá prechádza bodom  .
.
Pre mocnosť bodu
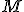 , ktorý leží zvonka kružnice
, ktorý leží zvonka kružnice 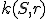 , platí rovnosť
, platí rovnosť 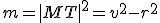 . Bod
. Bod 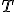 je dotykový bod dotyčnice, ktorá prechádza bodom
je dotykový bod dotyčnice, ktorá prechádza bodom  .
.
Dôkaz vety 2 ilustrujeme ako limitný prechod vo veta 1.
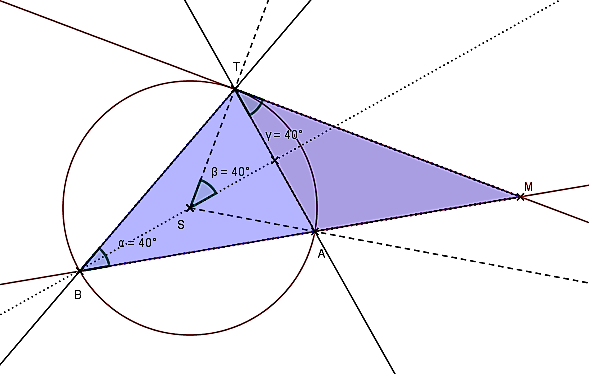 Pomocou obrázka urobte korektný matematický dôkaz. Využite podobnosť trojuholníkov
Pomocou obrázka urobte korektný matematický dôkaz. Využite podobnosť trojuholníkov 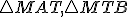 , ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí
, ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí 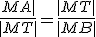 .
.
Pri odvodení vzťahu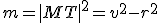 môžeme využiť skutočnosť, že trojuholník
môžeme využiť skutočnosť, že trojuholník 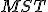 je pravouhlý a použiť Pytagorovu vetu.
je pravouhlý a použiť Pytagorovu vetu.
- Vzťah
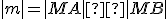 platí pro ľubovoľnú sečnicu.
platí pro ľubovoľnú sečnicu. - Pohybujme sečnicou tak, aby sa postupne blížila k dotyčnici v bode
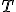 .
. - Bod
 i bod
i bod  sa blížia k bodu
sa blížia k bodu 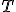 .
. - Veľkosť úsečky
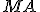 sa blíži k veľkosti úsečky
sa blíži k veľkosti úsečky 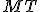 .
. - Z toho usudzujeme, že súčin
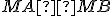 sa blíži k súčinu
sa blíži k súčinu 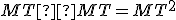 .
.

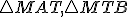 , ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí
, ktoré majú zhodné uhly. Pre pomery odpovedajúcich strán platí 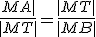 .
.
Pri odvodení vzťahu
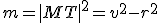 môžeme využiť skutočnosť, že trojuholník
môžeme využiť skutočnosť, že trojuholník 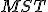 je pravouhlý a použiť Pytagorovu vetu.
je pravouhlý a použiť Pytagorovu vetu.
Definícia (Chordála a chordický bod).
Majme dve nesústredné kružnice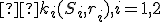 . Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
. Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
Majme dve nesústredné kružnice
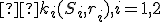 . Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
. Množina všetkých bodov, ktoré majú rovnakú mocnosť k obom kružniciam je priamka kolmá k spojnici stredov týchto kružníc. Nazývame ju chordála.
Korektnosť definície a konštrukcia chordály.
- Dané kružnice
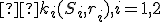 sa pretínajú v dvoch bodoch/priesečníkoch. Priamka určená priesečníkmi daných kružníc je spoločná sečnica oboch kružníc. Preto ľubovoľný bod priamky určenej týmito priesečníkmi má rovnakú mocnosť k obom kružniciam. Priamka určená priesečníkmi daných kružníc je chordála daných kružníc.
sa pretínajú v dvoch bodoch/priesečníkoch. Priamka určená priesečníkmi daných kružníc je spoločná sečnica oboch kružníc. Preto ľubovoľný bod priamky určenej týmito priesečníkmi má rovnakú mocnosť k obom kružniciam. Priamka určená priesečníkmi daných kružníc je chordála daných kružníc. - Kružnice sa dotýkajú v bode, ktorý má mocnosť
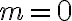 k obom kružniciam. Chordála je spoločná dotyčnica v bode. Dôkaz, že spoločná dotyčnica je množina bodov s rovnakou mocnosťou k obom kružniciam, vyplýva z vety 2.
k obom kružniciam. Chordála je spoločná dotyčnica v bode. Dôkaz, že spoločná dotyčnica je množina bodov s rovnakou mocnosťou k obom kružniciam, vyplýva z vety 2. - V prípade, že kružnice nemajú spoločný bod zvoľme pomocnú kružnicu
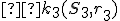 , ktorá pretína obe kružnice
, ktorá pretína obe kružnice 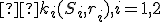 . Zostrojme chordály
. Zostrojme chordály 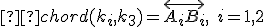 . Ich priesečník označme
. Ich priesečník označme 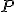 . Tento bod má rovnakú mocnosť ku všetkým trom kružniciam. Nazývame ho chordický bod. Týmto bodom potom vedieme kolmicu k úsečke, čo je chordála kružníc
. Tento bod má rovnakú mocnosť ku všetkým trom kružniciam. Nazývame ho chordický bod. Týmto bodom potom vedieme kolmicu k úsečke, čo je chordála kružníc 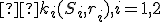 . Aktivujte si priložený applet.
. Aktivujte si priložený applet.