Neeuklidovská geometria
Neeuklidovská geometria
V historickom vývoji geometrie nájdeme dva východiskové míľniky, ktoré by sme mohli charakterizovať tromi otázkami:
„Ako to vytvoriť? “
„Prečo to platí?“
„Platí piaty Euklidov postulát?“
Pozrite si práce [GRE], [VAL].
„Ako to vytvoriť? “
„Prečo to platí?“
„Platí piaty Euklidov postulát?“
Pozrite si práce [GRE], [VAL].
- Začiatok tejto cesty „Ako “ patrí približne do obdobia dvoch tisícročí pred naším letopočtom, do obdobia mezopotámskeho a egyptského staroveku.
- Obdobie „Prečo“ zahŕňa obdobie od antického Grécka až po objavy neeuklidovských geometrií. S úctou k velikánom gréckej matematiky a filozofie treba zdôrazniť, že mnohé grécke myšlienky predbehli svoju dobu o dve nasledujúce tisícročia.
„Väčšina ľudí nevie, že v 19. storočí došlo k revolúcii v oblasti geometrie, ktorá bola vedecky tak hlboká a
vo svojom vplyve rovnako filozoficky dôležitá ako Darwinova evolučná teória.“
Prenikaním informačno-komunikačných technológií (IKT) do života spoločnosti koncom 20. storočia nášho letopočtu sa začala revolúcia nielen v myslení ľudí ale aj v organizácii a riadení ich práce. Používanie IKT vo vzdelávacom procese sa stalo neodmysliteľnou súčasťou moderného vyučovania. V tejto práci chceme poukázať na nové možnosti riešenia konštrukčných úloh v hyperbolickej neeuklidovskej geometrie využitím nových nástrojov v programe GeoGebra. Zameriame sa na model Poincare Disc, v ktorom budeme riešiť základné geometrické úlohy len použitím "neeuklidovského" pravítka a kružítka.
Definícia.
Neeuklidovská geometria je taká geometria, v ktorej neplatí piaty Euklidov postulát (axióma rovnobežnosti) ale spĺňa axiómy incidencie, usporiadania a zhodnosti.
Neeuklidovská geometria je taká geometria, v ktorej neplatí piaty Euklidov postulát (axióma rovnobežnosti) ale spĺňa axiómy incidencie, usporiadania a zhodnosti.
Neeuklidovské geometrie rozdeľujeme do dvoch kategórií:
- Hyperbolická geometria, v ktorej daným bodom neležiacim na danej priamke prechádzajú aspoň dve rovnobežky.
- Parabolická geometria, v ktorej neexistuje žiadna rovnobežka idúca daným bodom neležiacim na danej priamke.
V našej práci sa budeme zaoberať len hyperbolickou rovinnou geometriou.
Za východisko pre hyperbolickú rovinu si vezmeme dvojdielny hyperboloid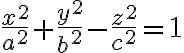 .
.
Uskutočníme dve operácie:
Za východisko pre hyperbolickú rovinu si vezmeme dvojdielny hyperboloid
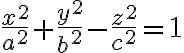 .
.
Uskutočníme dve operácie:
- Operácia "stotožnenie" každých dvoch bodov hyperboloidu súmerných podľa jeho stredu. Takouto operáciou redukujeme daný hyperboloid len na jednu jeho časť. Takto definovanú dvojicu bodov nazývame združené body. V ďalších úvahách budeme pracovať len s jeho jednou časťou hyperboloidu, napríklad s "hornou časťou".
- Operácia "prienik" bude predstavovať rez hyperboloidu stredovou rovinou, ktorá je určená dvomi rôznymi bodmi (dvomi združenými dvojicami bodov) a stredom hyperboloidu. Teoreticky stredová rovina môže byť trojakého typu: reálne pretína hyperboloid v hyperbole, môže sa dotýkať hyperboloidu alebo ho nepretína v reálnom prieniku.
- Bod hyperbolickej roviny je trojakého typu:
- vlastný bod hyperboloidu je dvojica
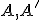 združených bodov, ktorú nazývame h-bod
združených bodov, ktorú nazývame h-bod - nevlastný (limitný) bod
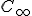 hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný bod 1. druhu
hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný bod 1. druhu - nevlastné body priestoru Euklidovského priestoru, ktoré na ploche hyperboloidu neležia, nazývame nevlastný bod 2. druhu Napríklad bod
 (spolu so združeným bodom A') hyperboloidu je vlastný
h-bod hyperbolickej roviny.
(spolu so združeným bodom A') hyperboloidu je vlastný
h-bod hyperbolickej roviny.
- vlastný bod hyperboloidu je dvojica
- Priamka hyperbolickej roviny je krivka, ktorá vznikne ako prienik (rez) hyperboloidu
s ľubovoľnou stredovou rovinou1). Keďže rezy takých rovín môžu byť trojakého typu, existujú tri typy hyperbolických h-priamok.
- ak prienikom stredovej roviny s hyperboloidom je hyperbola, tak túto krivku (hyperbolu) nazývame h-priamka
- ak prienik obsahuje len povrchovú priamku asymptotickej2) kužeľovej plochy (rovina sa dotýka hyperboloidu v nekonečne), tak tento prienik budeme považovať za nevlastnú h-priamku 1. druhu (rovina hyperboloid reálne pretne v komplexne združených rovnobežkách)
- nepretína hyperboloid, tak rezom je imaginárna kužeľosečka (elipsa), ktorú nazveme nevlastná h-priamka 2. druhu.
Poznámky.
- Stredová rovina (priamka) je rovina (priamka) prechádzajúca stredom
 hyperboloidu.
hyperboloidu. - Asymptotická kužeľová plocha je rotačná plocha, ktorá sa dotýka rotačného hyperboloidu v nevlastnej kužeľosečke.
- Nevlastný (limitný) bod
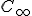 hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu.
hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu. - Nevlastné body priestoru Euklidovského priestoru, ktoré na ploche hyperboloidu neležia, nazývame nevlastný h-bod 2. druhu.
- Keďže rezy stredových rovín s hyperboloidom môžu byť trojakého typu, existujú tri typy hyperbolických h-priamok:
- ak prienik obsahuje len povrchovú priamku asymptotickej kužeľovej plochy (rovina sa dotýka hyperboloidu v nekonečne), tak tento prienik budeme považovať za nevlastnú h-priamku 1. druhu (rovina hyperboloid reálne pretne v komplexne združených rovnobežkách)
- ak stredová rovina nepretína hyperboloid, tak rezom je imaginárna kužeľosečka (elipsa), ktorú nazveme nevlastná h-priamka 2. druhu.
