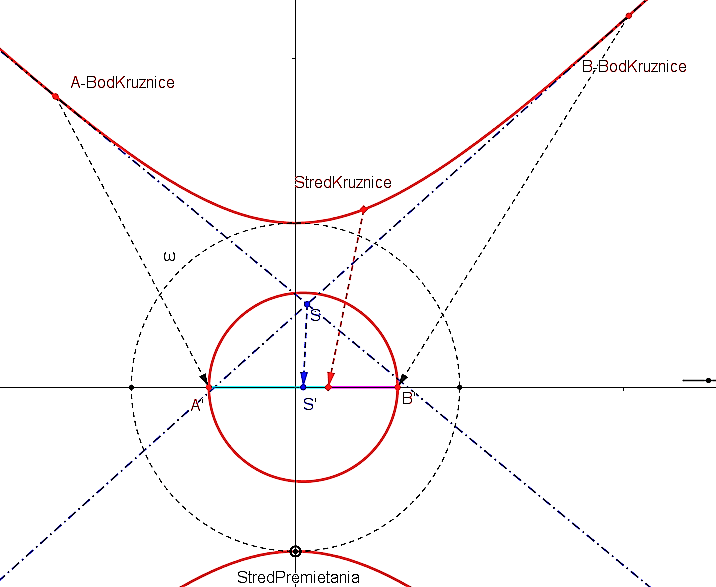
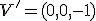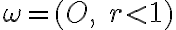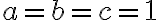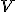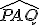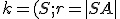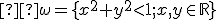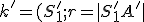Neeuklidovská geometria
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Neeuklidovská geometria |
| Vytlačil(a): | Visiteur anonyme |
| Dátum: | streda, 3 júla 2024, 11:39 |
Neeuklidovská geometria
V historickom vývoji geometrie nájdeme dva východiskové míľniky, ktoré by sme mohli charakterizovať tromi otázkami:
„Ako to vytvoriť? “
„Prečo to platí?“
„Platí piaty Euklidov postulát?“
Pozrite si práce [GRE], [VAL].
„Ako to vytvoriť? “
„Prečo to platí?“
„Platí piaty Euklidov postulát?“
Pozrite si práce [GRE], [VAL].
- Začiatok tejto cesty „Ako “ patrí približne do obdobia dvoch tisícročí pred naším letopočtom, do obdobia mezopotámskeho a egyptského staroveku.
- Obdobie „Prečo“ zahŕňa obdobie od antického Grécka až po objavy neeuklidovských geometrií. S úctou k velikánom gréckej matematiky a filozofie treba zdôrazniť, že mnohé grécke myšlienky predbehli svoju dobu o dve nasledujúce tisícročia.
„Väčšina ľudí nevie, že v 19. storočí došlo k revolúcii v oblasti geometrie, ktorá bola vedecky tak hlboká a
vo svojom vplyve rovnako filozoficky dôležitá ako Darwinova evolučná teória.“
Prenikaním informačno-komunikačných technológií (IKT) do života spoločnosti koncom 20. storočia nášho letopočtu sa začala revolúcia nielen v myslení ľudí ale aj v organizácii a riadení ich práce. Používanie IKT vo vzdelávacom procese sa stalo neodmysliteľnou súčasťou moderného vyučovania. V tejto práci chceme poukázať na nové možnosti riešenia konštrukčných úloh v hyperbolickej neeuklidovskej geometrie využitím nových nástrojov v programe GeoGebra. Zameriame sa na model Poincare Disc, v ktorom budeme riešiť základné geometrické úlohy len použitím "neeuklidovského" pravítka a kružítka.
Definícia.
Neeuklidovská geometria je taká geometria, v ktorej neplatí piaty Euklidov postulát (axióma rovnobežnosti) ale spĺňa axiómy incidencie, usporiadania a zhodnosti.
Neeuklidovská geometria je taká geometria, v ktorej neplatí piaty Euklidov postulát (axióma rovnobežnosti) ale spĺňa axiómy incidencie, usporiadania a zhodnosti.
Neeuklidovské geometrie rozdeľujeme do dvoch kategórií:
- Hyperbolická geometria, v ktorej daným bodom neležiacim na danej priamke prechádzajú aspoň dve rovnobežky.
- Parabolická geometria, v ktorej neexistuje žiadna rovnobežka idúca daným bodom neležiacim na danej priamke.
V našej práci sa budeme zaoberať len hyperbolickou rovinnou geometriou.
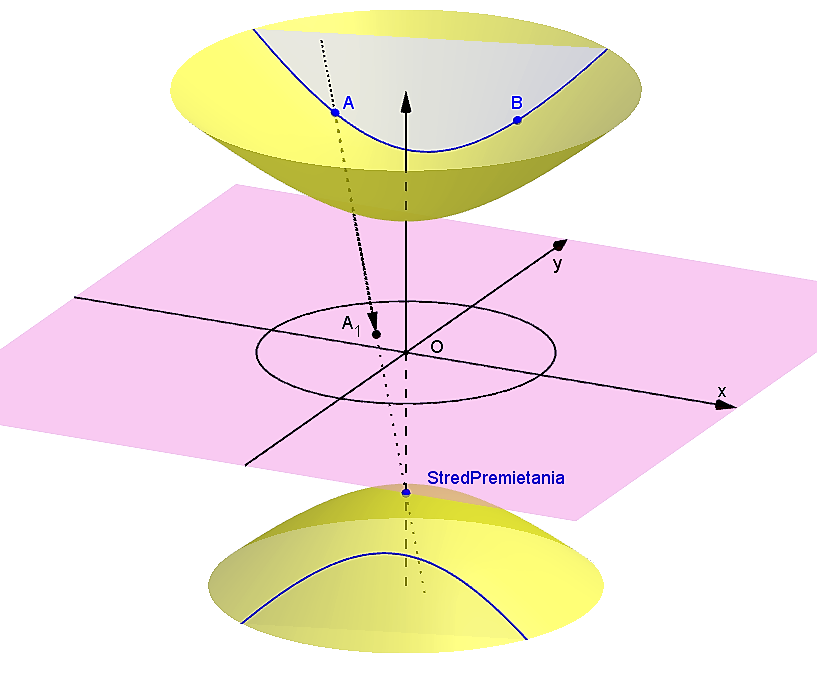
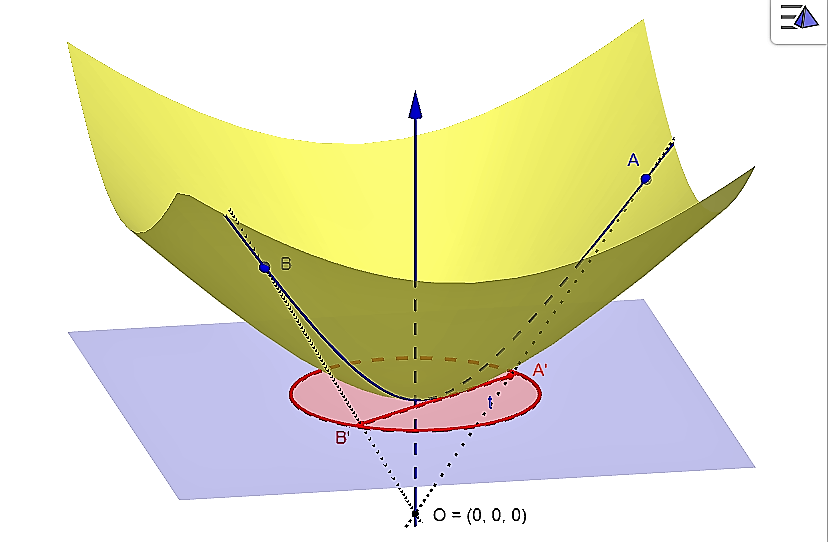
Za východisko pre hyperbolickú rovinu si vezmeme dvojdielny hyperboloid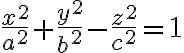 .
.
Uskutočníme dve operácie:
Za východisko pre hyperbolickú rovinu si vezmeme dvojdielny hyperboloid
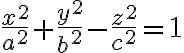 .
.
Uskutočníme dve operácie:
- Operácia "stotožnenie" každých dvoch bodov hyperboloidu súmerných podľa jeho stredu. Takouto operáciou redukujeme daný hyperboloid len na jednu jeho časť. Takto definovanú dvojicu bodov nazývame združené body. V ďalších úvahách budeme pracovať len s jeho jednou časťou hyperboloidu, napríklad s "hornou časťou".
- Operácia "prienik" bude predstavovať rez hyperboloidu stredovou rovinou, ktorá je určená dvomi rôznymi bodmi (dvomi združenými dvojicami bodov) a stredom hyperboloidu. Teoreticky stredová rovina môže byť trojakého typu: reálne pretína hyperboloid v hyperbole, môže sa dotýkať hyperboloidu alebo ho nepretína v reálnom prieniku.
- Bod hyperbolickej roviny je trojakého typu:
- vlastný bod hyperboloidu je dvojica
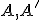 združených bodov, ktorú nazývame h-bod
združených bodov, ktorú nazývame h-bod - nevlastný (limitný) bod
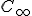 hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný bod 1. druhu
hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný bod 1. druhu - nevlastné body priestoru Euklidovského priestoru, ktoré na ploche hyperboloidu neležia, nazývame nevlastný bod 2. druhu Napríklad bod
 (spolu so združeným bodom A') hyperboloidu je vlastný
h-bod hyperbolickej roviny.
(spolu so združeným bodom A') hyperboloidu je vlastný
h-bod hyperbolickej roviny.
- vlastný bod hyperboloidu je dvojica
- Priamka hyperbolickej roviny je krivka, ktorá vznikne ako prienik (rez) hyperboloidu
s ľubovoľnou stredovou rovinou1). Keďže rezy takých rovín môžu byť trojakého typu, existujú tri typy hyperbolických h-priamok.
- ak prienikom stredovej roviny s hyperboloidom je hyperbola, tak túto krivku (hyperbolu) nazývame h-priamka
- ak prienik obsahuje len povrchovú priamku asymptotickej2) kužeľovej plochy (rovina sa dotýka hyperboloidu v nekonečne), tak tento prienik budeme považovať za nevlastnú h-priamku 1. druhu (rovina hyperboloid reálne pretne v komplexne združených rovnobežkách)
- nepretína hyperboloid, tak rezom je imaginárna kužeľosečka (elipsa), ktorú nazveme nevlastná h-priamka 2. druhu.
Poznámky.
- Stredová rovina (priamka) je rovina (priamka) prechádzajúca stredom
 hyperboloidu.
hyperboloidu. - Asymptotická kužeľová plocha je rotačná plocha, ktorá sa dotýka rotačného hyperboloidu v nevlastnej kužeľosečke.
- Nevlastný (limitný) bod
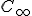 hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu.
hyperboloidu (stotožnené body na nevlastnej kružnici) nazývame nevlastný h-bod 1. druhu. - Nevlastné body priestoru Euklidovského priestoru, ktoré na ploche hyperboloidu neležia, nazývame nevlastný h-bod 2. druhu.
- Keďže rezy stredových rovín s hyperboloidom môžu byť trojakého typu, existujú tri typy hyperbolických h-priamok:
- ak prienik obsahuje len povrchovú priamku asymptotickej kužeľovej plochy (rovina sa dotýka hyperboloidu v nekonečne), tak tento prienik budeme považovať za nevlastnú h-priamku 1. druhu (rovina hyperboloid reálne pretne v komplexne združených rovnobežkách)
- ak stredová rovina nepretína hyperboloid, tak rezom je imaginárna kužeľosečka (elipsa), ktorú nazveme nevlastná h-priamka 2. druhu.
Modely
Poincarè model
Tvrdenie
Dôkaz
- Dôkaz prvej časti tohto tvrdenia vyplýva z vlastností stredového premietania, v ktorom sa kužeľová plocha obaľujúca hyperboloid zobrazí do kružnice
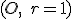 . To znamená, že ľubovoľný bod hyperboloidu sa zobrazí do vnútra kruhu
. To znamená, že ľubovoľný bod hyperboloidu sa zobrazí do vnútra kruhu 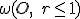 .
. - Dôkaz druhej časti o priemete h-priamky (reálne stredovej hyperboly) rozdelíme na dve etapy i. a ii.
- Nech
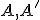 je dvojica združených bodov hyperboloidu a nech
je dvojica združených bodov hyperboloidu a nech 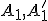 sú ich stredové priemety. Pre súčin vzdialeností
sú ich stredové priemety. Pre súčin vzdialeností
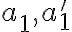 bodov
bodov 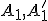 od stredu
od stredu  hyperboloidu platí:
hyperboloidu platí:
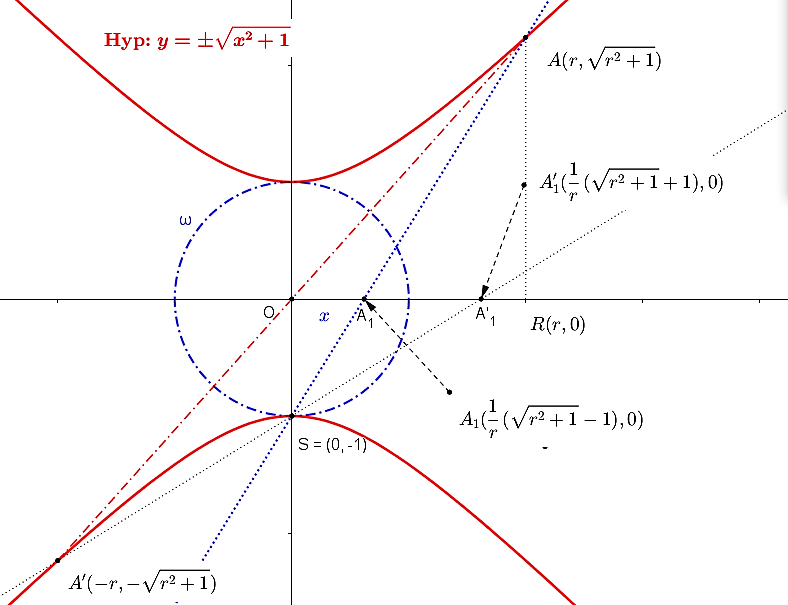
![a_1 \times a'_1=[ \frac{1}{r}(\sqrt{r^2+1}-1)] \times [\frac{1}{r}(\sqrt{r^2+1}+1)]=1 a_1 \times a'_1=[ \frac{1}{r}(\sqrt{r^2+1}-1)] \times [\frac{1}{r}(\sqrt{r^2+1}+1)]=1](https://lms.umb.sk/filter/tex/pix.php/bd6f2c6a62689c2e552273cc589b6f51.png) .
.
Dôkaz toho, že súčin vzdialeností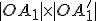 je konštantný je prezentovaný v nižšie priloženom applete.
je konštantný je prezentovaný v nižšie priloženom applete.
- Musíme ešte dokázať, že priemety h-bodov
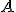 h-priamky (hyperboly) v označení
h-priamky (hyperboly) v označení 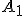 ležia na kružnici kolmej na kružnicu
ležia na kružnici kolmej na kružnicu 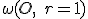 . Dôkaz je v ďalšej kapitole tejto práce. Pri dôkaze budeme potrebovať tvrdenie o mocnosti bodu ku kružnici.
. Dôkaz je v ďalšej kapitole tejto práce. Pri dôkaze budeme potrebovať tvrdenie o mocnosti bodu ku kružnici.
- Nech
Mocnosť bodu ku kružnici
Je daná kružnica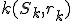 a bod
a bod  , ležiaci zvonka kružnice. Nech
, ležiaci zvonka kružnice. Nech  je sečnica kružnice
je sečnica kružnice  vedená bodom
vedená bodom  a
nech
a
nech 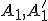 sú priesečníky sečnice
sú priesečníky sečnice  s kružnicou
s kružnicou 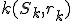 .
Pod mocnosťou bodu
.
Pod mocnosťou bodu  ku kružnici
ku kružnici 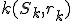 rozumieme číslo
rozumieme číslo 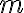 , pre ktoré platí:
, pre ktoré platí: 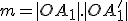 .
.
Je daná kružnica
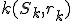 a bod
a bod  , ležiaci zvonka kružnice. Nech
, ležiaci zvonka kružnice. Nech  je sečnica kružnice
je sečnica kružnice  vedená bodom
vedená bodom  a
nech
a
nech 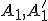 sú priesečníky sečnice
sú priesečníky sečnice  s kružnicou
s kružnicou 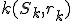 .
Pod mocnosťou bodu
.
Pod mocnosťou bodu  ku kružnici
ku kružnici 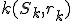 rozumieme číslo
rozumieme číslo 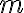 , pre ktoré platí:
, pre ktoré platí: 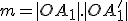 .
.
Viac o mocnosti bodu ku kružnice nájdete v kurze Planimetria a stereometria Tu. Vlastnosť mocnosť stačí vhodne aplikovať na náš prípad. Ilustráciu tvrdenia o priemete h-priamky prezentuje nasledujúci applete. Podrobný dôkaz (časti ii.) nájde čitateľ v ďalšej podkapitole s názvom "Hyperbolická priamka". Pozrite si tiež kapitolu "The Poincaré Disk Model" v práci [HIT].
Beltramiho-Kleinov model
Model vznikne ako stredový priemet dvojdielneho hyperboloidu do roviny kolmej na os hyperboloidu, pričom
Model vznikne ako stredový priemet dvojdielneho hyperboloidu do roviny kolmej na os hyperboloidu, pričom
Zhrnutie
- Bodmi Beltrami Kleinovho modelu sú body Klein Disku.
- Priamkami sú tetivy tohto disku.
V obidvoch hyperbolických modeloch (Beltrami a Poincarè) neplatí axióma rovnobežnosti.
- V obidvoch prípadoch existuje viac ako jedna rovnobežka.
- Existencia rovnobežky vyplýva z prvých skupín axióm.
- V modeli "Sféra" nemáme zaručenú ani existenciu rovnobežky.
- Kleinov disk a Poincarè disk sú modely, ktoré vzniknú aj premietaním do vhodnej roviny. Pozri Disk a hyperboloid.
- Výhodou modelu Klein je, že priamky v tomto modeli sú euklidovské (rovné) tetivy. Nevýhodou je, že model nie je konformný (kruhy a uhly sú skreslené).
- Neeuklidovská hyperbolická geometria reprezentovaná Poincarè diskom je konformná.
Hyperbolická priamka
Pokračovanie dôkazu tvrdenia o priemete h-priamky, v ktorom využijeme tvrdenie o mocnosti bodu ku kružnici.
Tvrdenie
Priemetom h-priamky (hyperboly) do Poincarè disku je otvorený kružnicový oblúk, ktorý je kolmý na hranicu kruhu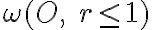 .
.
Pri dôkaze budeme potrebovať aj pojem dvojice inverzných bodov a pojem polárneho prvku v kruhovej inverzii. Viac o kruhovej inverzii nájdete v kurze Planimetria a stereometria
Tu. Najskôr dokážeme lemu:
Priemetom h-priamky (hyperboly) do Poincarè disku je otvorený kružnicový oblúk, ktorý je kolmý na hranicu kruhu
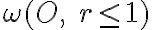 .
.
Lema
Nech je daná kruhová inverzia určená kružnicou - hranicou kruhu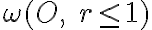 a nech bod
a nech bod 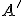 je obrazom bodu
je obrazom bodu 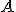 v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu
v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu  prechádzajúcu dvojicou inverzných bodov
prechádzajúcu dvojicou inverzných bodov 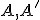 . Ak kružnica
. Ak kružnica  pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu
pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu 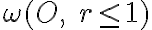 , tak kružnica
, tak kružnica  pretína kružnicu - hranicu kruhu
pretína kružnicu - hranicu kruhu 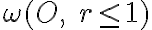 kolmo.
kolmo.
Nech je daná kruhová inverzia určená kružnicou - hranicou kruhu
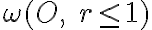 a nech bod
a nech bod 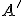 je obrazom bodu
je obrazom bodu 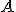 v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu
v tejto kruhovej inverzii. Zvoľme si ľubovoľnú ale pevne zvolenú kružnicu  prechádzajúcu dvojicou inverzných bodov
prechádzajúcu dvojicou inverzných bodov 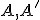 . Ak kružnica
. Ak kružnica  pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu
pozostáva výlučne len z dvojíc inverzných bodov vzhľadom na
kružnicu - hranicu kruhu 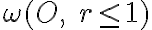 , tak kružnica
, tak kružnica  pretína kružnicu - hranicu kruhu
pretína kružnicu - hranicu kruhu 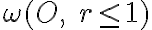 kolmo.
kolmo.
Dôkaz
V dôsledku lemy a predchádzajúcich častí dôkazu môžeme vysloviť tvrdenie.
- Nech body
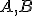 sú priemety bodov h-priamky
sú priemety bodov h-priamky 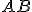 . Pozrite si priložený obrázok.
. Pozrite si priložený obrázok. - Podľa predchádzajúcej časti dôkazu (i.) platí
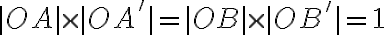 .
. - Odkiaľ: bod
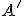 je obrazom bodu
je obrazom bodu 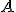 aj v kruhovej inverzii
aj v kruhovej inverzii 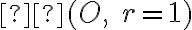 . Podobne to môžeme povedať aj o bodoch
. Podobne to môžeme povedať aj o bodoch 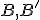 .
. - Nech
 je kružnica určená bodmi
je kružnica určená bodmi 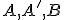 , potom v dôsledku mocnosti bodu
, potom v dôsledku mocnosti bodu 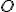 ku kružnici
ku kružnici  bude aj bod
bude aj bod 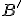 bodom kružnice
bodom kružnice  .
. - Teraz uvažujme o dotykových bodoch
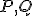 na dotyčniciach z bodu
na dotyčniciach z bodu 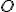 ku kružnici
ku kružnici  .
. - Mocnosť bodov
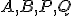 ku kružnici
ku kružnici 
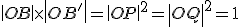
- Z toho vyplýva, že body
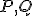 sú samodružné v kruhovej inverzii
sú samodružné v kruhovej inverzii 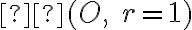 .
. - Priamky
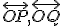 sú dotyčnice ku kružnici
sú dotyčnice ku kružnici  . Odkiaľ
. Odkiaľ 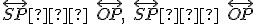 .
. - Kružnica
 je kolmá na kružnicu
je kolmá na kružnicu 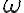 .
Tým je dôkaz lemy ukončený.
.
Tým je dôkaz lemy ukončený.
V dôsledku lemy a predchádzajúcich častí dôkazu môžeme vysloviť tvrdenie.
Poincarè diskový model (tiež sa používa označenie
Poincarè Disc) hyperbolickej roviny je prezentovaný v euklidovskej rovine ako
otvorený kruh
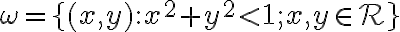 . Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
. Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
V predchádzajúcej časti sme uviedli, že tento otvorený kruh je stredovým priemetom dvojdielneho hyperboloidu. Uviedli sme tvrdenie, že v Poincarè diskovom modeli pre hyperbolické body a hyperbolické priamky platí:
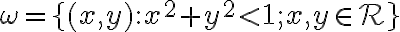 . Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
. Euklidovskú geometriu roviny môžeme považovať za „ontológiu pozadia“.
V predchádzajúcej časti sme uviedli, že tento otvorený kruh je stredovým priemetom dvojdielneho hyperboloidu. Uviedli sme tvrdenie, že v Poincarè diskovom modeli pre hyperbolické body a hyperbolické priamky platí:
- vlastný bod je vnútorný bod kruhu, ktorý je priemetom vlastného h-bodu hyperboloidu;
- koncový bod (resp. nevlastný bod) ležiaci na hranici kruhu, ktorý je priemetom nevlastného bodu 1. druhu;
- priamka je otvorený kružnicový oblúk kruhu - je priemetom h-priamky (hyperboly), pričom tento oblúk leží na kružnici kolmej na hranicu kruhu
Pri zostrojovaní hyperbolickej priamky určenej dvoma bodmi kruhu s výhodou využijeme vlastnosti kruhovej inverzie a konštrukcie popísané v predchádzajúcom dôkaze.
Poznámky
- V ďalšej podkapitole navrhneme v prostredí GeoGebra konštrukciu a zároveň aj nástroj na zostrojenie hyperbolickej priamky určenej dvoma rôznymi bodmi v Poincarè modeli disku. V konštrukcii využijeme inverzné body.
- Pri riešení konštrukčných úloh v Poincarè modeli potrebujeme okrem konštrukcie hyperbolickej priamky potrebovať aj konštrukciu kružnice a ďalších základných euklidovských konštrukcií (kolmica, os úsečky a pod).
Nástroj hPriamka
Poznámky.
- Konštrukcie v Poincarè Disku si uľahčíme, ak v GeoGebre vytvoríme vlastné nástroje, ktorými sa "vykreslí" resp. zostrojí požadovaný útvar.
- Vychádzame z tvrdenia, že h-priamka sa zobrazí do kružnicového oblúku, ktorý leží na kružnici kolmej k Poincarè disku.
- Najskôr musíme popísať konštrukciu, ktorá vytvorí požadovaný kolmý oblúk (obraz h-priamky).
- Potom pomocou makier vytvoríme nástroj, pomocou ktorého sa zostrojí požadovaný kolmý oblúk.
Príklad (Vytvorenie nástroja).
Daný je kruh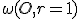 a body
a body 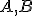 ležiace vnútri kruhu, pričom úsečka
ležiace vnútri kruhu, pričom úsečka 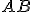 nie je priemerom. Zostrojte obraz hyperbolickej h-priamky určenej bodmi
nie je priemerom. Zostrojte obraz hyperbolickej h-priamky určenej bodmi 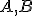 v prostredí GeoGebra.
v prostredí GeoGebra.
Daný je kruh
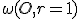 a body
a body 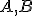 ležiace vnútri kruhu, pričom úsečka
ležiace vnútri kruhu, pričom úsečka 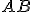 nie je priemerom. Zostrojte obraz hyperbolickej h-priamky určenej bodmi
nie je priemerom. Zostrojte obraz hyperbolickej h-priamky určenej bodmi 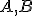 v prostredí GeoGebra.
v prostredí GeoGebra.
Riešenie - zostrojenie kružnicového oblúka v Euklidovskej rovine
Predpokladajme, že aspoň jeden z bodov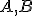 je vnútorný bod kruhu
je vnútorný bod kruhu 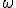 a je rôzny od stredu
a je rôzny od stredu 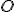 . Podľa už dokázaného tvrdenie je hľadaná h-priamka kružnicový oblúk, ktorý je určený bodmi
. Podľa už dokázaného tvrdenie je hľadaná h-priamka kružnicový oblúk, ktorý je určený bodmi 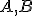 a zároveň leží na kružnici kolmej ku kruhu
a zároveň leží na kružnici kolmej ku kruhu 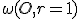 . Pozrite si nasledujúci obrázok.
. Pozrite si nasledujúci obrázok.
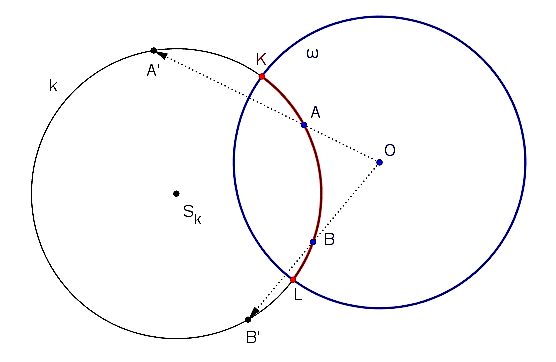
Postup euklidovskej konštrukcie.
Postup na vytvorenie nástroja "hPriamka" v GeoGebre, pomocou ktorého sa narysuje obraz hyperbolickej priamky v Poincarè modeli.
Predpokladajme, že aspoň jeden z bodov
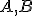 je vnútorný bod kruhu
je vnútorný bod kruhu 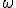 a je rôzny od stredu
a je rôzny od stredu 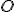 . Podľa už dokázaného tvrdenie je hľadaná h-priamka kružnicový oblúk, ktorý je určený bodmi
. Podľa už dokázaného tvrdenie je hľadaná h-priamka kružnicový oblúk, ktorý je určený bodmi 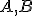 a zároveň leží na kružnici kolmej ku kruhu
a zároveň leží na kružnici kolmej ku kruhu 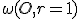 . Pozrite si nasledujúci obrázok.
. Pozrite si nasledujúci obrázok.

Postup euklidovskej konštrukcie.
- V kruhovej inverzii
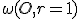 zostrojíme obrazy
zostrojíme obrazy 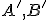 bodov
bodov 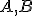 .
. - Zostrojíme kružnicu
 určenú bodmi
určenú bodmi 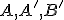 alebo bodmi
alebo bodmi 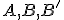 . Nájdeme priesečníky
. Nájdeme priesečníky 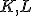 .
. - Na kružnici
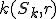 vyznačíme menší z oblúkov, ktoré sú určené krajnými bodmi
vyznačíme menší z oblúkov, ktoré sú určené krajnými bodmi 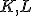 .
. - Menší oblúk je hľadaný obraz hyperbolickej priamky
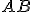 . Túto konštrukciu si otvoríte
Tu.
. Túto konštrukciu si otvoríte
Tu.
- úsečka
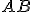 je priemerom kružnice
je priemerom kružnice 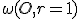 - v konštrukcii tento prípad má názov "Diameter"
- v konštrukcii tento prípad má názov "Diameter" - obidva body
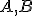 ležia na kružnici
ležia na kružnici 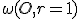 ale nie sú priemerom - v konštrukcii tento prípad má názov "Nevlastne",
nájdete v nami vytvorenom applete Tu.
ale nie sú priemerom - v konštrukcii tento prípad má názov "Nevlastne",
nájdete v nami vytvorenom applete Tu.
Postup na vytvorenie nástroja "hPriamka" v GeoGebre, pomocou ktorého sa narysuje obraz hyperbolickej priamky v Poincarè modeli.
- Spustite program GeoGebra a otvorte si súbor uložený s názvom "h-Priamka".
- V základnom Menu programu GeoGebra vyberte možnosť "Vytvoriť nový nástroj".
- Postupujte podľa pokynov pre vytvorenie nástroja:
- ako výstupné objekty vyberte oblúk "hPriamka" (otvorte si aj algebraické okno)
- ako vstupné objekty vyberte body:

- vhodne pomenujte nástroj, napr. "hPriamka", vyberte predtým vytvorený obrázok pre ikonu
- v nápovedi uveďte napr. "Ukáž dva body a potom klikni na kružnicu"
- zaškrtnite políčko "Ukázať na palete nástrojov" (nie je nutné).
- Ak už vidíte novú ikonku nástroja hPriamka, tak v tejto konštrukcii kliknite v stĺpci Súbor na Nový.
- Nákresňa je "čistá" ale ikonka hPriamka je tam (ak nie, tak Prispôsobte paletu nástrojov) . Teraz si vytvorte kružnicu
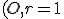 a
vhodne zväčšite plochu nárysne. Uložte si tento súbor napr. s názvom Nástroj hPriamka.
a
vhodne zväčšite plochu nárysne. Uložte si tento súbor napr. s názvom Nástroj hPriamka.
Nami novovytvorený nástroj hPriamka v GeoGebre na zostrojenie obrazu h-priamky v modeli
Poincaré Disc 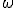 s polomerom
s polomerom 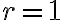 si môžete otvoriť
Tu (je umiestnený vpravo na lište nástrojov).
si môžete otvoriť
Tu (je umiestnený vpravo na lište nástrojov).
Používanie nástroja hPriamka je analogické ako v euklidovskej rovine. Najskôr si zvoľte dva rôzne body vo vnútri kruhu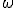 - pomocou nástroja Bod.
Potom aktivujte nástroj hPriamka a program vykreslí kružnicový oblúk, ktorý je priemetom h-priamky (hyperboly).
- pomocou nástroja Bod.
Potom aktivujte nástroj hPriamka a program vykreslí kružnicový oblúk, ktorý je priemetom h-priamky (hyperboly).
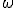 s polomerom
s polomerom 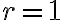 si môžete otvoriť
Tu (je umiestnený vpravo na lište nástrojov).
si môžete otvoriť
Tu (je umiestnený vpravo na lište nástrojov).
Používanie nástroja hPriamka je analogické ako v euklidovskej rovine. Najskôr si zvoľte dva rôzne body vo vnútri kruhu
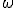 - pomocou nástroja Bod.
Potom aktivujte nástroj hPriamka a program vykreslí kružnicový oblúk, ktorý je priemetom h-priamky (hyperboly).
- pomocou nástroja Bod.
Potom aktivujte nástroj hPriamka a program vykreslí kružnicový oblúk, ktorý je priemetom h-priamky (hyperboly).
Cvičenie.
Vytvorte Nástroj/Ikonu v GeoGebre, pomocou ktorého sa vykreslí obraz hyperbolickej úsečky (časti hyperboly) v modeli Poincarè Disku.
Využite kompletnú konštrukciu hPriamky.
Pokračujte v tejto konštrukcii krokmi:
Vytvorte Nástroj/Ikonu v GeoGebre, pomocou ktorého sa vykreslí obraz hyperbolickej úsečky (časti hyperboly) v modeli Poincarè Disku.
Využite kompletnú konštrukciu hPriamky.
Pokračujte v tejto konštrukcii krokmi:
- zostrojte stred oblúka "hPriamka", ktorý označte napr.
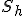
- potom zostrojte oblúk s názvom "hUsecka" určený stredom
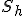 a krajnými bodmi
a krajnými bodmi  a
a - následne vytvorte GeoGebra nástroj s rovnakým názvom "hUsecka".
Nástroj hKružnica
Nech sú dané dva rôzne body  a
a  na hyperboloide.
na hyperboloide.
 a
a  na hyperboloide.
na hyperboloide. - Uvažujme o kružnici
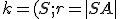 , ktorej všetky body sú bodmi hyperboloidu. Symbolicky:
, ktorej všetky body sú bodmi hyperboloidu. Symbolicky: 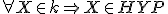 .
. - Nech bod
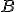 je stredovo súmerný k bodu
je stredovo súmerný k bodu  podľa stredu
podľa stredu  , potom bod
, potom bod 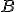 je tiež bodom kružnice
je tiež bodom kružnice  a zároveň bodom hyperboloidu.
a zároveň bodom hyperboloidu. - Nech
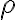 je určená bodmi
je určená bodmi 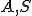 a bodom StredPremietania. Táto rovina pretína daný dvojdielny hyperboloid v hyperbole (v applete červená krivka).
a bodom StredPremietania. Táto rovina pretína daný dvojdielny hyperboloid v hyperbole (v applete červená krivka). - Zostrojme dotyčnice k tejto hyperbole v bodoch
 a ich priesečník
a ich priesečník 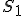 .
. - Potom platí nasledujúce tvrdenie, ktoré uvádzame bez dôkazu. K dôkazu sú potrebné širšie znalosti stredového premietania kužeľosečiek.
Poznámka.
Na základe tohto tvrdenia môžeme uskutočniť konštrukciu, pomocou ktorej zostrojíme kružnicu v Poincaré disku určenú stredom a bodom
a bodom  a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
Na základe tohto tvrdenia môžeme uskutočniť konštrukciu, pomocou ktorej zostrojíme kružnicu v Poincaré disku určenú stredom
 a bodom
a bodom  a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
a na základe tejto konštrukcie aj nástroj v GeoGebre pomocou, ktorého narysujeme kružnicu v modeli Poincaré Disc.
Poznámka.
Teraz už máme tri základné (euklidovské) nástroje: hPriamku hUsecku a hKružnicu v Geogebre.
Teraz už máme tri základné (euklidovské) nástroje: hPriamku hUsecku a hKružnicu v Geogebre.
Poincare disk
Základné "hyperbolické" konštrukcie v Poincarè Disku 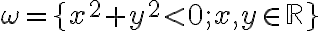 , ktoré sú zovšeobecnením euklidovských konštrukcií, sú prezentované formou riešených úloh. Pri riešení úloh z z neeuklidovskej geometrie je vhodné, aby ste si najskôr stiahli applet "Poincaré Disk" vytvorený v prostredí GeoGebra. Pomocou tohto appletu vieme zostrojiť hyperbolickú úsečku a priamku; kružnicu určenú stredom a bodom resp. polomerom; vieme určiť vzdialenosť dvoch bodov.
, ktoré sú zovšeobecnením euklidovských konštrukcií, sú prezentované formou riešených úloh. Pri riešení úloh z z neeuklidovskej geometrie je vhodné, aby ste si najskôr stiahli applet "Poincaré Disk" vytvorený v prostredí GeoGebra. Pomocou tohto appletu vieme zostrojiť hyperbolickú úsečku a priamku; kružnicu určenú stredom a bodom resp. polomerom; vieme určiť vzdialenosť dvoch bodov.
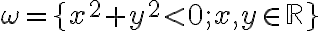 , ktoré sú zovšeobecnením euklidovských konštrukcií, sú prezentované formou riešených úloh. Pri riešení úloh z z neeuklidovskej geometrie je vhodné, aby ste si najskôr stiahli applet "Poincaré Disk" vytvorený v prostredí GeoGebra. Pomocou tohto appletu vieme zostrojiť hyperbolickú úsečku a priamku; kružnicu určenú stredom a bodom resp. polomerom; vieme určiť vzdialenosť dvoch bodov.
, ktoré sú zovšeobecnením euklidovských konštrukcií, sú prezentované formou riešených úloh. Pri riešení úloh z z neeuklidovskej geometrie je vhodné, aby ste si najskôr stiahli applet "Poincaré Disk" vytvorený v prostredí GeoGebra. Pomocou tohto appletu vieme zostrojiť hyperbolickú úsečku a priamku; kružnicu určenú stredom a bodom resp. polomerom; vieme určiť vzdialenosť dvoch bodov.
Riešené úlohy z neeuklidovskej geometrie.
- Zostrojte rovnostranný trojuholník
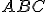 pomocou hyperbolických kružníc
pomocou hyperbolických kružníc 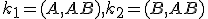 (pozrite si Euklidovo tvrdenie T/I).
(pozrite si Euklidovo tvrdenie T/I).
Riešenie Tu. - Zostrojte hyperbolickú priamku
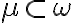 , ktorá je osou úsečky
, ktorá je osou úsečky 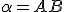 , kde
, kde 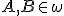 .
.
Návod:- Využitím Euklidovho tvrdenia T/I zostrojte hyperbolické rovnostranné trojuholník
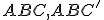 , kde
, kde 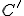 je súmerný bod podľa priamky
je súmerný bod podľa priamky 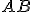 .
. - V trojuholníku
 zostrojte os prechádzajúcu vrcholmi
zostrojte os prechádzajúcu vrcholmi 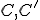 .
. - Využite Euklidove tvrdenia T/IX a T/X.
- Riešenie Tu.
- Využitím Euklidovho tvrdenia T/I zostrojte hyperbolické rovnostranné trojuholník
- Zostrojte hyperbolickú kolmicu
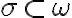 na hyperbolickú priamku
na hyperbolickú priamku 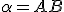 , ktorá prechádza bodom
, ktorá prechádza bodom 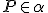 .
Pomocou dotyčníc k hPriamkam
.
Pomocou dotyčníc k hPriamkam 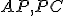 ukážte, že uhly pri päte kolmice sú pravé.
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
ukážte, že uhly pri päte kolmice sú pravé.
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
- Zostrojte hyperbolickú rovnobežku k hyperbolickej priamke
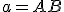 , ktorá prechádza bodom
, ktorá prechádza bodom 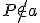 . Využite vlastnosť striedavých uhlov.
. Využite vlastnosť striedavých uhlov.
Poznámka.
Euklidove tvrdenia využívané v tejto časti platia aj v hyperbolickej geometrii, keďže sú nezávislé na piatom Euklidovom postuláte.
Euklidove tvrdenia využívané v tejto časti platia aj v hyperbolickej geometrii, keďže sú nezávislé na piatom Euklidovom postuláte.
Cvičenie I
Cvičenie.
- Zostrojte rovnoramenný trojuholník
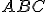 so základňou
so základňou 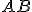 pomocou dvoch zhodných hyperbolických kružníc (kružnice s rovnakým polomerom).
Pomocou dotyčníc k hPriamkam
pomocou dvoch zhodných hyperbolických kružníc (kružnice s rovnakým polomerom).
Pomocou dotyčníc k hPriamkam 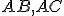 a k hPriamkam
a k hPriamkam 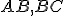 určte veľkosti uhlov pri základni a presvedčte sa, že majú rovnakú veľkosť. Riešenie Tu.
určte veľkosti uhlov pri základni a presvedčte sa, že majú rovnakú veľkosť. Riešenie Tu. - Nájdite stred kružnice(pozrite si Euklidovo tvrdenie: Kniha III, T/I). Riešenie Tu.
- Zostrojte hyperbolickú kolmicu
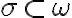 na hyperbolickú priamku
na hyperbolickú priamku 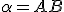 , ktorá neprechádza bodom
, ktorá neprechádza bodom 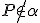 .
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
.
Návod: Využite Euklidove tvrdenia T/XI a T/XII.
- Zostrojte kružnicu vpísanú (resp. opísanú) do trojuholníka
 (pozrite si Euklidovo tvrdenie: Kniha IV, T/IV (resp. T/V)).
(pozrite si Euklidovo tvrdenie: Kniha IV, T/IV (resp. T/V)).
Základné hyperbolické konštrukcie v Poincare Disku
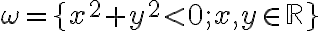 .
.
Poznámky.
- Pri dokazovaní prípadov 1a, 1b najskôr ukážte existenciu daného útvaru a potom jeho jednoznačnosť.
- Cvičenie 2. Ukážte, že základňa trojuholníka
 je stranou pravidelného päťuholníka vpísaného do kružnice
je stranou pravidelného päťuholníka vpísaného do kružnice  a rameno trojuholníka je jeho uhlopriečkou.
a rameno trojuholníka je jeho uhlopriečkou.
- Kolmé kružnice. Základ Tu. Kompletná konštrukcia Tu. GeoGebra s nástrojom "Kolmá kružnica" je Tu.