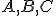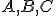Geometria trojuholníka
Geometria trojuholníka
Definícia (trojuholník v Hibertovom axiomatickom systéme).
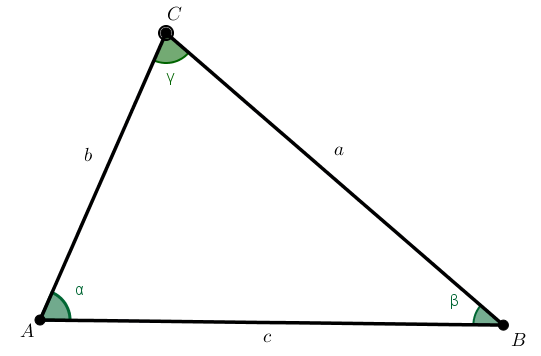
Nech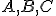 sú dané nekolineárne body. Pod trojuholníkom
sú dané nekolineárne body. Pod trojuholníkom  rozumieme prienik
polrovín
rozumieme prienik
polrovín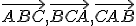 .
.
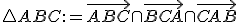
Nech
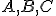 sú dané nekolineárne body. Pod trojuholníkom
sú dané nekolineárne body. Pod trojuholníkom  rozumieme prienik
polrovín
rozumieme prienik
polrovín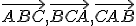 .
.
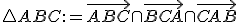
Základné pojmy.
Poznámky.
Za základné vety (vlastnosti) trojuholníka považujeme nasledujúce dve vety:
- Veta o súčte vnútorných uhlov v trojuholníku.
- Trojuholníkovú nerovnosť.
Veta (Súčet vnútorných uhlov).
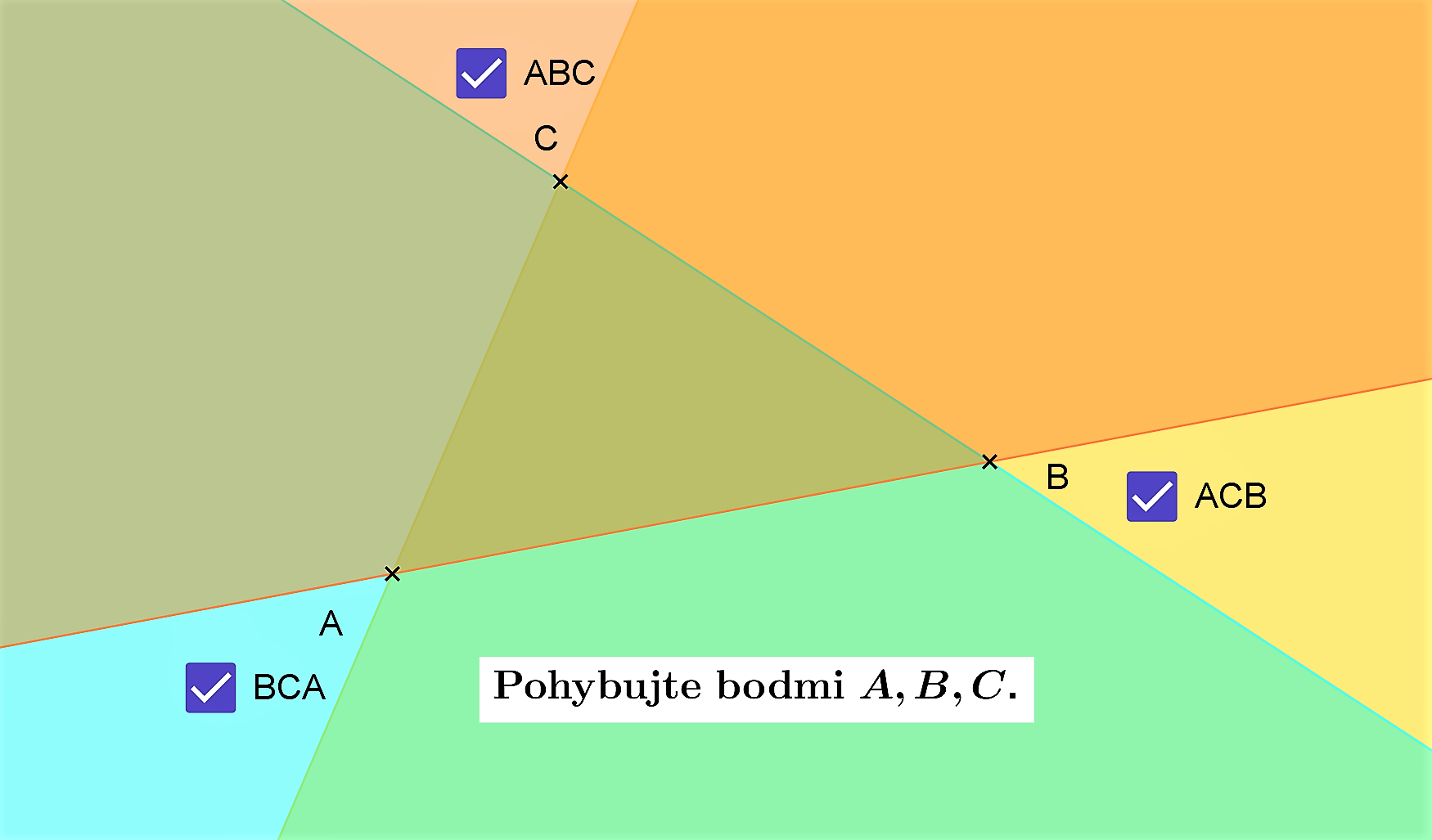
Súčet všetkých vnútorných uhlov v trojuholníku je priamy uhol (veľkosť je rovná 180°).
Súčet všetkých vnútorných uhlov v trojuholníku je priamy uhol (veľkosť je rovná 180°).
Euklides pri dôkaze tejto vety sa opiera o tvrdenia (pozrite si podkapitolu Vety o trojuholníku)
- T/XXIX - "Priamka pretínajúca rovnobežky vytvára striedavé zhodné uhly a vonkajší uhol sa rovná opačnému vnútornému uhlu a súčet vnútorných uhlov na tej istej strane sa rovná dvom pravým uhlom."
- T/XXXI - "Daným bodom je možné zostrojiť priamku rovnobežnú s danou priamkou"
Interpretácia - existuje mnoho appletov, ktoré interpretujú vetu o súčte vnútorných uhlov. Aktivujte si dva, v ktorých:
Euklidov dôkaz - applet Tu.