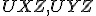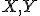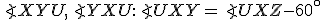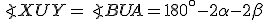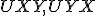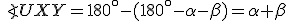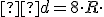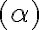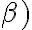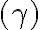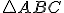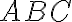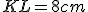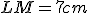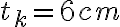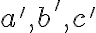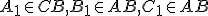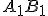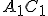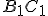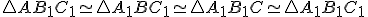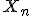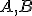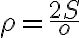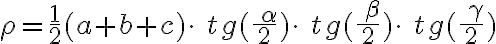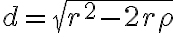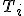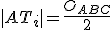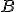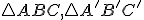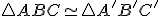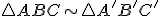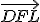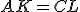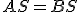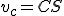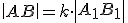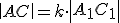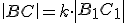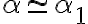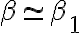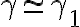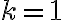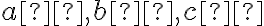Geometria trojuholníka
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Planimetria a stereometria |
| Kniha: | Geometria trojuholníka |
| Vytlačil(a): | Visiteur anonyme |
| Dátum: | streda, 3 júla 2024, 11:16 |
Geometria trojuholníka
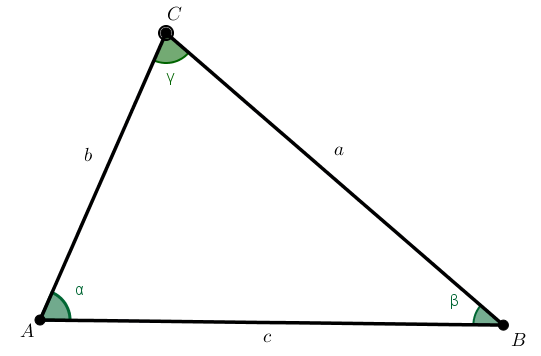
Definícia (trojuholník v Hibertovom axiomatickom systéme).
Nech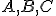 sú dané nekolineárne body. Pod trojuholníkom
sú dané nekolineárne body. Pod trojuholníkom  rozumieme prienik
polrovín
rozumieme prienik
polrovín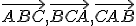 .
.
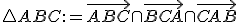
Nech
 sú dané nekolineárne body. Pod trojuholníkom
sú dané nekolineárne body. Pod trojuholníkom  rozumieme prienik
polrovín
rozumieme prienik
polrovín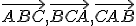 .
.
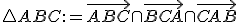
Základné pojmy.
Poznámky.
Za základné vety (vlastnosti) trojuholníka považujeme nasledujúce dve vety:
- Veta o súčte vnútorných uhlov v trojuholníku.
- Trojuholníkovú nerovnosť.
Veta (Súčet vnútorných uhlov).
Súčet všetkých vnútorných uhlov v trojuholníku je priamy uhol (veľkosť je rovná 180°).
Súčet všetkých vnútorných uhlov v trojuholníku je priamy uhol (veľkosť je rovná 180°).
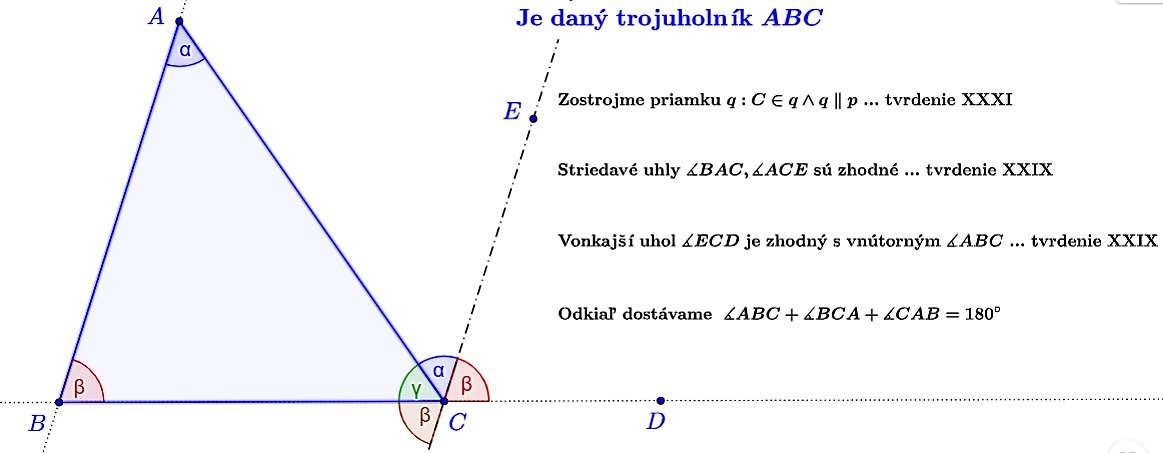
Euklides pri dôkaze tejto vety sa opiera o tvrdenia (pozrite si podkapitolu Vety o trojuholníku)
- T/XXIX - "Priamka pretínajúca rovnobežky vytvára striedavé zhodné uhly a vonkajší uhol sa rovná opačnému vnútornému uhlu a súčet vnútorných uhlov na tej istej strane sa rovná dvom pravým uhlom."
- T/XXXI - "Daným bodom je možné zostrojiť priamku rovnobežnú s danou priamkou"
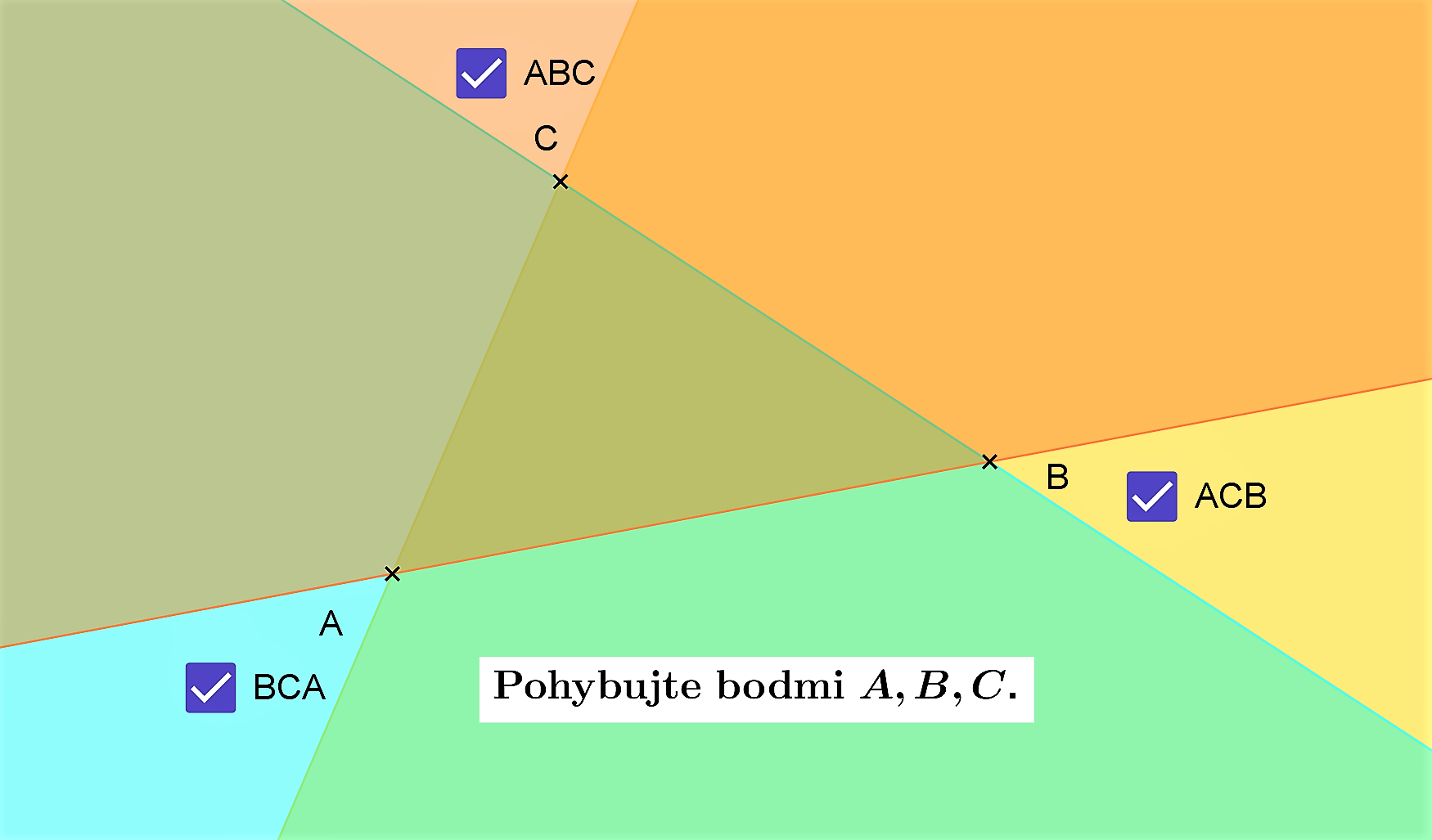
Interpretácia - existuje mnoho appletov, ktoré interpretujú vetu o súčte vnútorných uhlov. Aktivujte si dva, v ktorých:
Euklidov dôkaz - applet Tu.
Kategorizácia trojuholníkov
Trojuholníky môžeme rozčleniť podľa viacerých kritérií, napríklad podľa:
- dĺžky jeho strán
- veľkosti najväčšieho vnútorného uhla.
Vzhľadom na dĺžky (veľkosti) strán v danom trojuholníku rozdeľujeme trojuholníky do troch skupín
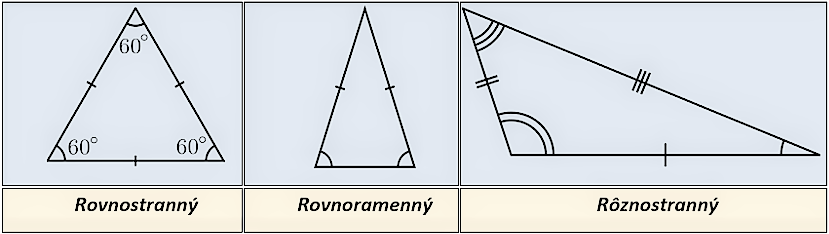
- Rovnostranný trojuholník - všetky strany trojuholníka majú rovnakú dĺžku (sú navzájom zhodné).
- Rovnoramenný trojuholník - práve (len) dve strany rovnakej dĺžky (sú navzájom zhodné).
- Rôznostranný trojuholník - všetky strany majú rozličnú dĺžku (žiadne dve strany trojuholníka nie sú zhodné).
Poznámka
Zdôvodnenie, že neexistuje viac druhov trojuholníkov vyplýva z dichotomického hľadiska. Pre tri veľkosti strán (resp. pre tri čísla: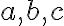 môžu nastať len prípady:
môžu nastať len prípady:
1.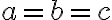 , 2.
, 2.
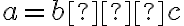 , 3.
, 3.
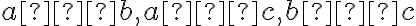
Zdôvodnenie, že neexistuje viac druhov trojuholníkov vyplýva z dichotomického hľadiska. Pre tri veľkosti strán (resp. pre tri čísla:
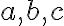 môžu nastať len prípady:
môžu nastať len prípady:
1.
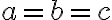 , 2.
, 2.
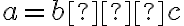 , 3.
, 3.
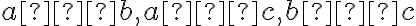
Vzhľadom na veľkosti veľkosti najväčšieho vnútorného uhla rozdeľujeme trojuholníky do troch skupín

- Ostrouhlý trojuholník – má všetky vnútorné uhly menšie ako 90° (tri ostré uhly).
- Pravouhlý trojuholník – má práve jeden vnútorný uhol s veľkosťou 90° (jeden pravý uhol).
- Tupouhlý trojuholník – má práve jeden vnútorný uhol väčší ako 90° (tupý uhol) a ostatné uhly má ostré.
V priloženom applete "Rozdelenie trojuholníkov" môžete generovať rôzne typy trojuholníkov tak, že budete pohybovať vrcholmi trojuholníka. Vytvorte rôzne typy trojuholníkov, ktoré sú charakterizované veľkosťou strán a veľkosťou uhlov. Nájdite napríklad takú polohu vrcholov trojuholníka, aby bol pravouhlý a súčasne rovnoramenný (ak taký existuje). Pokúste sa zodpovedať otázku: Koľko rôznych typov trojuholníkov reálne vznikne?
Úloha.
Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Práca [LAR] (Larson, Príklad 8.1.16, Tu)
Nájdite dĺžku strany rovnostranného trojuholníka, ktorého vrcholy majú od nejakého vnútorného bodu vzdialenosti 5, 7, 8. Práca [LAR] (Larson, Príklad 8.1.16, Tu)
Riešenie.
- Geometrické modelovanie/riešenie pomocou GeoGebry vhodné aj pre základné školy.
- Konštrukčné riešenie
- Algebraické riešenie pomocou kosínusovej vety vhodné pre stredné školy
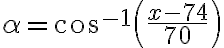
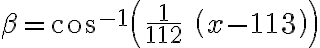
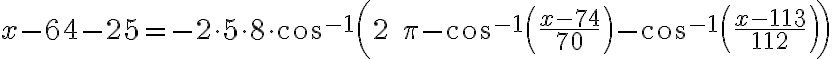 Applet Tu
Applet Tu
Vybrané vety o trojuholníkoch
Definícia (Deliaci pomer).
Nech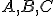 sú tri kolineárne body také, že
sú tri kolineárne body také, že 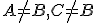 .
Deliaci pomer bodu
.
Deliaci pomer bodu  vzhľadom k bodom
vzhľadom k bodom 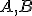 rozumieme reálne
číslo
rozumieme reálne
číslo 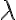 (označenie
(označenie 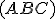 ), pre ktoré platí
), pre ktoré platí
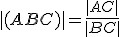 .
.
Pre bod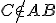 je
je 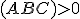 a pre bod
a pre bod 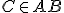 je
je 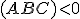 . Pre
. Pre 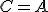 je zrejme
je zrejme 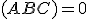 .
.
Nech
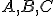 sú tri kolineárne body také, že
sú tri kolineárne body také, že 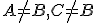 .
Deliaci pomer bodu
.
Deliaci pomer bodu  vzhľadom k bodom
vzhľadom k bodom 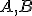 rozumieme reálne
číslo
rozumieme reálne
číslo 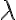 (označenie
(označenie 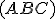 ), pre ktoré platí
), pre ktoré platí
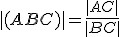 .
.Pre bod
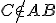 je
je 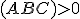 a pre bod
a pre bod 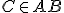 je
je 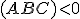 . Pre
. Pre 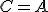 je zrejme
je zrejme 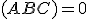 .
.
Poznámky.
- V niektorej literatúre sa pod deliacim pomerom troch rôznych kolineárnych bodov rozumie reálne číslo
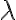 , pre ktoré platí:
, pre ktoré platí:
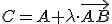 .
.
Takúto definíciu používa aj GeoGebra. - Deliaci pomer stredu úsečky je rovný -1. Dokážte to.
- Pre tri rôzne kolineárne body platí:
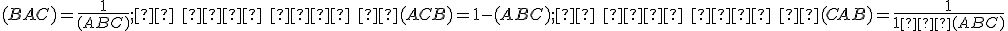 .
.
Dokážte to. - V rovine sú dané dva pevne body
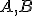 . Množina všetkých bodov
. Množina všetkých bodov 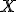 tejto roviny, pre ktoré platí
tejto roviny, pre ktoré platí
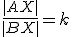 ,
,
kde je reálna konštanta, je kružnica. Dokážte to a vytvorte konštrukciu v GeoGebre.
je reálna konštanta, je kružnica. Dokážte to a vytvorte konštrukciu v GeoGebre.
Cevova veta.
V trojuholníku sa priamky
sa priamky 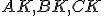 , kde
, kde 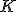 je vnútorným bodom trojuholníka
je vnútorným bodom trojuholníka  a
a
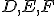 sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
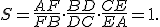
V trojuholníku
 sa priamky
sa priamky 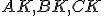 , kde
, kde 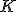 je vnútorným bodom trojuholníka
je vnútorným bodom trojuholníka  a
a
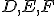 sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
sú body ležiace na stranách odpovedajúcim protiľahlým vrcholom trojuholníka, pretínajú v jednom bode práve vtedy, ak platí:
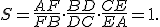
Giovanni Ceva bol taliansky matematik žijúci na prelome 17. a 18. storočia. Cevova veta stanovuje podmienku, kedy majú tri priamky prochádzajúce vrcholmi trojuholníka spoločný bod. Uvedieme jej prvú časť dôkazu, ktorý má konštrukčný charakter.
Dôkaz.
1. (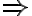 ): Ak sa priamky pretínajú v jednom bode, tak
): Ak sa priamky pretínajú v jednom bode, tak 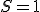 .
.
2. (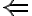 ): Ak
): Ak 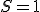 , tak sa priamky pretínajú v jednom bode.
, tak sa priamky pretínajú v jednom bode.
Pri dôkaze tejto implikácie sa vychádza z priesečníka dvoch priamok. Potom sa zostrojí priamka prechádzajúca týmto priesečníkom a tretím vrcholom. Následne sa dokáže, že táto priamka pretína protiľahlú stranu v bode, ktorý spĺňa podmienky vo vete. V dôkaze sa používajú tie isté podobnosti trojuholníkov ako v prvej časti dôkazu. Podrobnejší dôkaz nájdete v práci [Val, 2005].
Dôkaz.
1. (
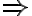 ): Ak sa priamky pretínajú v jednom bode, tak
): Ak sa priamky pretínajú v jednom bode, tak 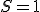 .
.
2. (
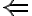 ): Ak
): Ak 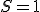 , tak sa priamky pretínajú v jednom bode.
, tak sa priamky pretínajú v jednom bode.
Pri dôkaze tejto implikácie sa vychádza z priesečníka dvoch priamok. Potom sa zostrojí priamka prechádzajúca týmto priesečníkom a tretím vrcholom. Následne sa dokáže, že táto priamka pretína protiľahlú stranu v bode, ktorý spĺňa podmienky vo vete. V dôkaze sa používajú tie isté podobnosti trojuholníkov ako v prvej časti dôkazu. Podrobnejší dôkaz nájdete v práci [Val, 2005].
Poznámky.
Aplikovaním Cévovej vety dokážte, že v ľubovoľnom trojuholníku sa:
Aplikovaním Cévovej vety dokážte, že v ľubovoľnom trojuholníku sa:
- Ťažnice sa pretínajú v jednom bode - ťažisku. (Využite skutočnosť, že ťažnice prechádzajú stredmi strán a každý z pomerov v Cévovej vete má tvar
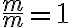 .)
.) - Výšky pretínajú v jednom bode - ortocentre. (Využite skutočnosť, že napr.
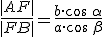 , ak
, ak 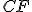 je výška.)
je výška.) - Osi vnútorných uhlov trojuholníka sa pretínajú v jednom bode - stred vpísanej kružnice. (Využite skutočnosť, že os vnútorného uhla rozdeľuje protiľahlú stranu na dve časti, ktorých dĺžky sú v rovnakom pomere ako im priľahlé strany trojuholníka.)
- Neskôr tieto tvrdenia dokážeme euklidovskou metódou.
Morleyho veta.
Ak v trojuholníku zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka
zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka 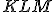 .
.
Ak v trojuholníku
 zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka
zostrojíme polpriamky, rozdeľujúce jeho vnútorné uhly na tretinové veľkosti, odpovedajúce si polpriamky sa pretínajú vo vrcholoch rovnostranného trojuholníka 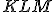 .
.
Morleyho veta predstavuje jednu z najprekvapujúcejších vlastností elementárnej geometrie, ktorú v roku 1899 objavil a dokázal anglo-americký matematik Frank Morley (1860-1937). Niektorí matematici nazývajú túto vetu aj ako Morleyov zázrak.
Poznámky.
- V 2. kroku dôkazu zhodnosť vyplýva z vety
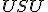 (uhly pri vrchole
(uhly pri vrchole 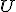 ... os uhla, pri vrchole
... os uhla, pri vrchole  majú veľkosť
majú veľkosť 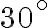 , strana
, strana 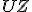 spoločná).
spoločná). - V 5. kroku dôkazu je potrebné ukázať, že trojuholník
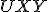 je rovnoramenný (uhly pri základni sú zhodné):
je rovnoramenný (uhly pri základni sú zhodné):
- Morleyova veta sa dá dokázať trigonometricky pomocou sínusovej a kosínusovej vety a vzorcov pre sčítanie uhlov.
Ťažisko trojuholníka
Definícia (Ťažnica trojuholníka).
Nech je daný trojuholník a nech
a nech
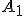 je stred strany
je stred strany
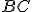 . Úsečka
. Úsečka
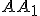 sa nazýva ťažnica
trojuholníka
sa nazýva ťažnica
trojuholníka
 .
.
Nech je daný trojuholník
 a nech
a nech
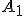 je stred strany
je stred strany
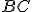 . Úsečka
. Úsečka
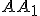 sa nazýva ťažnica
trojuholníka
sa nazýva ťažnica
trojuholníka
 .
.
V ďalších podkapitolách tejto sekcie dokážeme vlastnosti o ťažniciach trojuholníka.
Poznámky.
- Ťažnice trojuholníka
 budeme označovať
budeme označovať
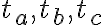 .
. - Krajný bod ťažnice
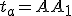 označujeme
označujeme 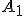 resp. používa sa označenie:
resp. používa sa označenie:
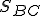 - stred strany
- stred strany
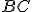 alebo
alebo
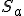 - stred strany
- stred strany
 .
. - Vlastnosť, že ťažisko rozdeľuje každú ťažnicu v pomere
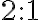 sa na ZŠ robí meraním, na stredných školách sa už dokazuje táto vlastnosť.
sa na ZŠ robí meraním, na stredných školách sa už dokazuje táto vlastnosť. - V príprave budúcich učiteľov matematiky sa prezentuje viacero dôkazov. Napríklad ako dôsledok Cevovej vety alebo pomocou osovej afinity transformujeme trojuholník na rovnostranný. Tiež sa využíva aj vhodná rovnoľahlosť
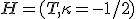 .
.
Pri hľadaní ťažiska trojuholníka sa sústredíme na skúmanie vlastností priečok rovnobežných s danou stranou trojuholníka.
Experiment.
Vytvorme v GeoGebre model trojuholníka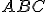 rozdeleného na veľmi tenké pásiky, ktoré budú rovnobežné so stranou
rozdeleného na veľmi tenké pásiky, ktoré budú rovnobežné so stranou 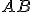 .
.
Vytvorme v GeoGebre model trojuholníka
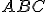 rozdeleného na veľmi tenké pásiky, ktoré budú rovnobežné so stranou
rozdeleného na veľmi tenké pásiky, ktoré budú rovnobežné so stranou 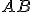 .
.- Zrejme ťažisko
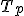 každého tenkého pásika bude ležať v jeho "strede"
každého tenkého pásika bude ležať v jeho "strede" - Pásiky budeme postupne zužovať, až dostaneme rovnobežné úsečky
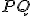 so stranou
so stranou
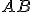
- Pri posúvaní rovnobežnej úsečky
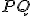 pomocou bodu
pomocou bodu
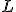 sa bude zaznamenávať stopa jej stredu
sa bude zaznamenávať stopa jej stredu
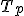
- Stopa ako množina všetkých stredov
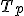 je zrejme úsečka
je zrejme úsečka
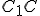 , kde
, kde
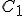 je stred strany
je stred strany
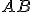
-
Ťažnica trojuholníka je množina všetkých stredov
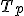 priečok
priečok
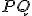
- Učiteľ nabáda žiakov, aby sformulovali otázky súvisiace s ťažnicami trojuholníka. Uvádzame niekoľko vhodných otázok:
Pokračujeme v ďalšom experimente a hľadajme odpovede na otázky:
Experimenty sú spracované podľa práce: [LUK] Lukáč, S.: Bádateľský prístup k výučbe trojuholníkov.(Dostupné Tu).
Experimenty sú spracované podľa práce: [LUK] Lukáč, S.: Bádateľský prístup k výučbe trojuholníkov.(Dostupné Tu).
Veta.
Ťažnice trojuholíka sa pretínajú v jedinom bode T, ktoré nazývame ťažisko.
Ťažnice trojuholíka sa pretínajú v jedinom bode T, ktoré nazývame ťažisko.
Konštrukčný dôkaz.
- Vyberieme (zvolíme si) dve ťažnice
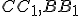
- Zostrojíme rovnobežky s týmito ťažnicami v bodoch
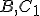 . Ich jednoznačnú existenciu zaručuje V. Euklidov postulát.
. Ich jednoznačnú existenciu zaručuje V. Euklidov postulát. - Zostrojíme priesečník
 týchto rovnobežiek. Vznikne rovnobežník, v ktorom uhlopriečky
týchto rovnobežiek. Vznikne rovnobežník, v ktorom uhlopriečky 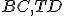 sa rozpoľujú.
sa rozpoľujú. - V trojuholníku
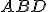 je
je 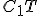 stredná, odkiaľ dostávame
stredná, odkiaľ dostávame 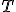 je stred
je stred 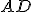 .
. - Podobne pre trojuholník
 je
je 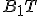 stredná priečka trojuholníka.
stredná priečka trojuholníka. - Z bodov 4 a 5 vyplýva, že priesečník
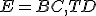 je stred strany. Teda
je stred strany. Teda 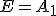 , čo bolo treba dokázať.
, čo bolo treba dokázať.
Urobte dôkaz pomocou Cevovej vety aj pomocou afinity. Pozrite si dôkaz od Martina Vinklera Tu.
Rozbor úlohy.
- V trojuholníku
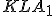 poznáme dĺžky všetkých strán
poznáme dĺžky všetkých strán 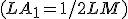
- Môžeme zostrojiť trojuholník
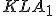 pomocou vety
pomocou vety 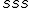
- Predĺžením strany
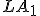 zostrojíme bod
zostrojíme bod 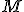
- urobte konštrukciu trojuholníka
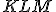 podľa vyššie uvedeného rozboru (náš návrh
Tu),
podľa vyššie uvedeného rozboru (náš návrh
Tu), - urobte diskusiu o počte riešení.
Výška a stredná priečka
Definícia.
Kolmica zostrojená z vrcholu trojuholníka na priamku, na ktorej leží protiľahlá strana trojuholníka, sa nazýva výška trojuholníka.
Kolmica zostrojená z vrcholu trojuholníka na priamku, na ktorej leží protiľahlá strana trojuholníka, sa nazýva výška trojuholníka.
Výšky trojuholníka  budeme označovať
budeme označovať 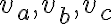 .
.

 budeme označovať
budeme označovať 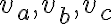 .
.
-
Výšky sa pretínajú v jednom bode
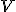 .
. - Tento bod sa nazýva priesečník výšok alebo ortocentrum, stiahnite si applet Tu
Úloha.
Zostrojte trojuholník, ak je daná výška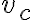 , uhol
, uhol 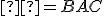 a uhol
a uhol 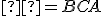 .
.
Zostrojte trojuholník, ak je daná výška
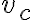 , uhol
, uhol 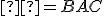 a uhol
a uhol 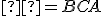 .
.
- Urobte rozbor tejto úlohy a porovnajte s návrhom v priloženom applete →.
- V priloženom applete deaktivujte Začiarkavacie políčko a navrhnite postup konštrukcie.
- Urobte symbolický zápis konštrukčných krokov v geometrickom okne 2, pozrite si náš návrh Tu →.
- Preveďte dôkaz správnosti konštrukcie a urobte diskusiu.
Albert Einstein
 → (Obrázok je prevzatý z Wikipédie)
→ (Obrázok je prevzatý z Wikipédie)
 → (Obrázok je prevzatý z Wikipédie)
→ (Obrázok je prevzatý z Wikipédie)
Keď som mal dvanásť rokov, zažil som zázrak iného druhu vďaka knižočke1) o Euklidovej geometrii roviny, ktorá sa mi dostala na začiatku školského roku do rúk.
- Boli to poučky, ako napríklad, že tri výšky v trojuholníku sa pretínajú v jednom bode.
- Hoci to nie je v nijakom prípade evidentné, predsa sa to dalo dokázať s takou istotou, že pochybnosť sa zdala byť vylúčená.
- Táto jasnosť a istota spravili na mňa neopísateľný dojem.
Veta (Ortocentrum trojuholníka).
Výšky v trojuholníku sa pretínajú v jednom bode.
Výšky v trojuholníku sa pretínajú v jednom bode.
Dôkaz, ktorý nadchol Einsteina.
 Applet otvoríte Tu.
Applet otvoríte Tu.
Vyššie uvedený dôkaz sa opiera o dve základné tvrdenia:
- V rovnobežníku protiľahlé strany majú rovnakú veľkosť. Pozrite si Euclid's Elements, Book I, Proposition 34.
- Priamka prechádzajúca stredom kruhu a stredom tetivy je kolmá na túto tetivu a rozpoľuje túto tetivu. Pozrite si Euclid's Elements, , Book III, Proposition 3. Toto tvrdenie bolo pravdepodobne známe už Thálesovi.
Veta.
Dôsledok.
- Stredná priečka trojuholníka je rovnobežná so stranou trojuholníka.
- Jej veľkosť sa rovná polovici veľkosti strany, s ktorou je rovnobežná.
Trojuholníkové centrum
Definícia.
Bod trojuholníka, ktorý je invariantný vzhľadom na rovnoľahlosť, sa nazýva trojuholníkové centrum (triangle Center).
Bod trojuholníka, ktorý je invariantný vzhľadom na rovnoľahlosť, sa nazýva trojuholníkové centrum (triangle Center).
Najznámejšie sú napríklad
Menej známe ale často využívané v konštrukciách sú Eulerova priamka a Feurbachova kružnica deviatich bodov.
Definícia (Eulerova priamka).
V ľubovoľnom trojuholníku, s výnimkou rovnostranného, ležia ortocentrum , ťažisko
, ťažisko 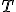 a stred opísanej kružnice
a stred opísanej kružnice
 S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí
S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí 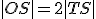 . V rovnostrannom trojuholníku body
. V rovnostrannom trojuholníku body
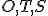 splývajú.
splývajú.
V ľubovoľnom trojuholníku, s výnimkou rovnostranného, ležia ortocentrum
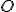 , ťažisko
, ťažisko 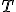 a stred opísanej kružnice
a stred opísanej kružnice
 S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí
S na jednej priamke, ktorú nazývame Eulerova priamka. Pre ich vzdialenosti platí 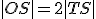 . V rovnostrannom trojuholníku body
. V rovnostrannom trojuholníku body
 splývajú.
splývajú.
Pozrite si dôkaz od Martina Vinklera, prípadne navrhnite iný dôkaz s využitím rovnoľahlosti Tu.
Definícia (Feuerbachova kružnica).
Nech je všeobecný trojuholník,
je všeobecný trojuholník, 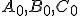 nech sú päty jeho výšok,
nech sú päty jeho výšok, 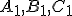 nech sú
stredy jeho strán,
nech sú
stredy jeho strán, 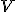 nech je priesečník výšok a
nech je priesečník výšok a 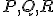 nech sú postupne stredy úsečiek
nech sú postupne stredy úsečiek 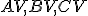 .
Potom
.
Potom  bodov
bodov  leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
Nech
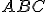 je všeobecný trojuholník,
je všeobecný trojuholník, 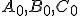 nech sú päty jeho výšok,
nech sú päty jeho výšok, 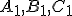 nech sú
stredy jeho strán,
nech sú
stredy jeho strán,  nech je priesečník výšok a
nech je priesečník výšok a  nech sú postupne stredy úsečiek
nech sú postupne stredy úsečiek 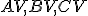 .
Potom
.
Potom 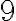 bodov
bodov 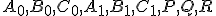 leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
leží na jednej kružnici, ktorú nazývame Feuerbachova kružnica.
Pozrite si konštrukčný dôkaz
Tu.
Definícia.
Kružnica, ktorá prechádza všetkými troma vrcholmi trojuholníka sa nazýva kružnica opísaná trojuholníku.
Kružnica, ktorá prechádza všetkými troma vrcholmi trojuholníka sa nazýva kružnica opísaná trojuholníku.
Konštrukčne pri hľadaní stredu opísanej kružnice postupujme takto:
- Zvolíme si ľubovoľné dve strany trojuholníka a zostrojíme ich osi .
- Priesečník týchto osí je stred
 kružnice opísanej trojuholníku
kružnice opísanej trojuholníku  .
. - Zároveň je nutné dokázať, že os tretej strany trojuholníka
 prechádza vždy týmto priesečníkom.
prechádza vždy týmto priesečníkom.
(dôkaz už poznal Tháles)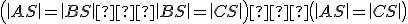 .
. - Z tejto konštrukcie vyplýva aj tvrdenie, že každému trojuholníku možno opísať práve jednu kružnicu.
- Kde leží stred kružnice opísanej u pravouhlých trojuholníkov?
Dôkaz uvádza Euklides v Knihe 1, Tvrdenie X., pozri kapitolu "Euklidovské konštrukcie".
Definícia.
-
Kružnica opísaná pravouhlému trojuholníku sa nazýva Tálesova kružnica.
Vlastnosti kružnice opísanej trojuholníku.
-
Veľkosť polomeru opísanej kružnice určuje vzťah
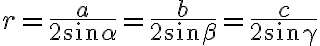
- Spojnica stredu opísanej kružnice a vrcholu trojuholníka je kolmá k strane jeho ortického trojuholníka (tzv. Nagelova veta →).
-
Kružnica deviatich bodov je rovnoľahlým obrazom opísanej kružnice so stredom rovnoľahlosti v ťažisku trojuholníka a koeficientom
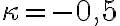 .
.
Definícia.
Ak z ľubovoľného bodu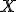 opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod
opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod 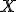 spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
Ak z ľubovoľného bodu
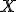 opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod
opísanej kružnice zostrojíme kolmice k jednotlivým stranám trojuholníka, tak päty týchto kolmíc budú ležať na jednej priamke. Túto priamku nazývame Simsonova priamka.
Ak bod 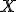 spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
spojíme s ortocentrom (priesečník výšok trojuholníka), tak Simsonova priamka prechádza stredom tejto úsečky.
Definícia.
Kružnica, ktorá sa dotýka všetkých strán daného trojuholníka sa nazýva vpísaná kružnica.
Vlastnosti
Definícia.
Kružnica, ktorá sa zvonka dotýka strany trojuholníka a dvoch priamok, ktoré sú predĺžením zvyšných strán trojuholníka sa nazýva
kružnica pripísaná trojuholníku.
Vlastnosti
Veta (Veta o osi vnútorného uhla).
V každom trojuholníku platí, že os vnútorného uhla delí protiľahlú stranu v rovnakom pomere, ako je pomer dĺžok príslušných priľahlých strán.
Cvičenie.
- Vyhľadajte v Euklidových Základoch tvrdenia - Kniha I. T/34 a Kniha III, T/3.
- Vyhľadajte v literatúre iné dôkazy vety o ortocentre trojuholníka.
Pytagorova a Euklidove vety
Veta (Pytagorova veta).
V každom pravouhlom trojuholníku , v ktorom prepona má veľkosť
, v ktorom prepona má veľkosť  a odvesny majú veľkosti
a odvesny majú veľkosti  platí
platí
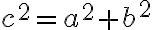 .
.
V každom pravouhlom trojuholníku
 , v ktorom prepona má veľkosť
, v ktorom prepona má veľkosť  a odvesny majú veľkosti
a odvesny majú veľkosti  platí
platí
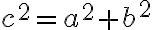 .
.
Slovná formulácia Pytagorovej vety:
Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
Pytagorova veta je pomenovaná podľa starogréckeho matematika Pytagora, ktorý ju odvodil v 6. storočí pred Kr.
Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
Pytagorova veta je pomenovaná podľa starogréckeho matematika Pytagora, ktorý ju odvodil v 6. storočí pred Kr.
- Dôkazov Pytagorovej vety existuje veľmi veľa, viac ako 300, pozri na GeoGebre Tu.
- Vyhľadajte pôvodný Euklidov dôkaz v Knihe I, tvrdenie T/XLVII)
- Pozrite si dôkaz Pytagorovej vety v programe GeoGebra, ktorý vychádza z Euklidovho dôkazu. Otvorte si applet Tu.
- Iné dôkazy Pytagorovej vety nájdeme na stránke M. Viklera alebo Wikipedia.
- Dôkaz "bez slov" →. Doplňte "slová" pre tento dôkaz - urobte slovné/písomné zdôvodnenie.
Poznámky.
- Pytagorova veta pravdepodobne bola známa aj v iných starovekých civilizáciách, napríklad v Číne, Egypte.
- Starí Egypťania stavali pozoruhodné stavby, pri ktorých potrebovali vytyčovať aj pravé uhly. Robili to takto:
Veta (Obrátená pytagorova veta).
Ak v trojuholníku platí pre dĺžky strán
platí pre dĺžky strán 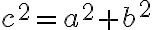 , tak tento trojuholník je pravouhlý s preponou
, tak tento trojuholník je pravouhlý s preponou  .
.
Ak v trojuholníku
 platí pre dĺžky strán
platí pre dĺžky strán 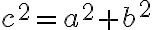 , tak tento trojuholník je pravouhlý s preponou
, tak tento trojuholník je pravouhlý s preponou  .
.
Príklad.
Dané sú sústredné kružnice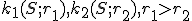 . Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami
. Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami 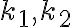 a obsahom kruhu nad tetivou
a obsahom kruhu nad tetivou 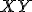 kružnice
kružnice 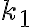 , ktorá sa dotýka kružnice
, ktorá sa dotýka kružnice 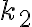 .
Riešenie
.
Riešenie
Preskúmajte súvislosť tejto úlohy s dôkazom Pytagorovej vety aplikáciou Mamikonovej vety (Wiki odkaz Tu). Otvorte si applet Tu
Dané sú sústredné kružnice
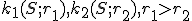 . Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami
. Určte vzťah medzi obsahom medzikružia ohraničeného
kružnicami 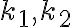 a obsahom kruhu nad tetivou
a obsahom kruhu nad tetivou 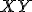 kružnice
kružnice 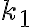 , ktorá sa dotýka kružnice
, ktorá sa dotýka kružnice 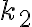 .
Riešenie
.
Riešenie
Preskúmajte súvislosť tejto úlohy s dôkazom Pytagorovej vety aplikáciou Mamikonovej vety (Wiki odkaz Tu). Otvorte si applet Tu
Pytagorova veta uvedená v Euklidových Základoch: Kniha 1, tvrdenie XLVII).
Veta (Pytagorova veta - znenie uvedené v Základoch).
V pravouhlých trojuholníkoch štvorec na strane oproti pravému uhlu ležiaci je rovný súčtu štvorcov na stranách, ktoré zvierajú pravý uhol.
V pravouhlých trojuholníkoch štvorec na strane oproti pravému uhlu ležiaci je rovný súčtu štvorcov na stranách, ktoré zvierajú pravý uhol.
Text Euklidovho dôkazu je spracovaný podľa českého prekladu od Františka Servíta z roku 1907, je doplnený o
(odkazy) na definície (Def.), axiómy (Post.), tvrdenia (T.) a Koncepcie / Zásady (Kon.)
Dôkaz.
-
 je pravouhlý trojuholník s pravým uhlom
je pravouhlý trojuholník s pravým uhlom 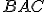 .
Hovorím, že štvorec na
.
Hovorím, že štvorec na 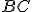 sa rovná (súčtom) štvorcov na
sa rovná (súčtom) štvorcov na 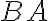 a
a 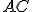 .
. - Nech je narysovaný
-
Bodom
 je vedená rovnobežka
je vedená rovnobežka 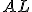 k
k 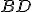 alebo k
alebo k
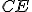 (T.31) a spojnice (úsečky)
(T.31) a spojnice (úsečky) 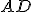 a
a 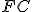 .
(Post.1)
.
(Post.1)
-
Vzhľadom na to, že každý z uhlov
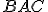 a
a 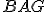 je pravý, z toho vyplýva, že priamkou
je pravý, z toho vyplýva, že priamkou
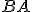 a bodom
a bodom  na ňom dve priame línie
na ňom dve priame línie 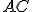 a
a 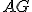 , ktoré nie sú
ležiace na tej istej strane, spôsobujú, že susedné uhly sa rovnajú dvom pravým uhlom
(Def.22)
, ktoré nie sú
ležiace na tej istej strane, spôsobujú, že susedné uhly sa rovnajú dvom pravým uhlom
(Def.22)
- Pretože uhol
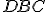 sa rovná uhlu
sa rovná uhlu 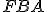 , pretože každý je pravý
(Post.4)
, pretože každý je pravý
(Post.4)
- Keďže
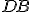 sa rovná
sa rovná 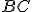 a
a 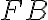 sa rovná
sa rovná
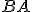 (Def.22),
(Def.22),
-
obe strany
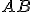 a
a 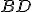 sa rovnajú obom stranám
sa rovnajú obom stranám 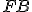 a
a  a
a
uhol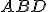 sa rovná uhlu
sa rovná uhlu 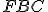 , preto základňa
, preto základňa 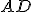 sa rovná základni
sa rovná základni 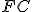 a
a
trojuholník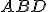 sa rovná (je zhodný) trojuholníku
sa rovná (je zhodný) trojuholníku 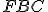 .
(T.4)
.
(T.4)
- Teraz rovnobežník
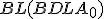 je dvakrát väčší ako trojuholník
je dvakrát väčší ako trojuholník
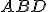 , pretože majú rovnakú základňu
, pretože majú rovnakú základňu 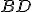 a
a
sú medzi tými istými rovnobežkami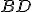 a
a 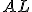 (majú spoločnú výšku).
(T.41)
(majú spoločnú výšku).
(T.41)
- A štvorec
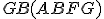 je dvakrát väčší ako trojuholník
je dvakrát väčší ako trojuholník
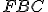 , pretože opäť majú rovnakú základňu
, pretože opäť majú rovnakú základňu 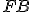 a
a
sú medzi tými istými rovnobežkami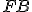 a
a 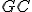 .
(T.41)
.
(T.41) - Preto sa rovnobežník
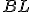 rovná štvorcu
rovná štvorcu 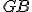 .
(Kon.2)
.
(Kon.2)
- Podobne, ak vedieme spojnice (úsečky)
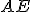 a
a
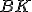 , rovnobežník
, rovnobežník 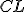 sa rovná štvorcu
sa rovná štvorcu  . Preto sa celý štvorec
. Preto sa celý štvorec
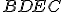 rovná súčtu dvoch štvorcov
rovná súčtu dvoch štvorcov 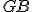 a
a 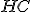 .
(Kon.2)
.
(Kon.2) -
A štvorec
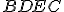 je narysovaný na
je narysovaný na 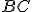 a štvorce
a štvorce 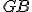 a
a 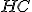 na
na
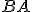 a
a 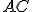 . Teda štvorec na
. Teda štvorec na 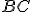 sa rovná súčtu štvorcov na
sa rovná súčtu štvorcov na 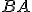 a
a 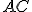 .
.
V dôkaze boli použité tieto zdroje z Euklidových Základov:
- Definícia 22: Zo štvorstranných útvarov je štvorec, ktorý je rovnako rovnostranný a pravouhlý; obdĺžnik, ktorý je pravouhlý, ale nie rovnostranný; kosoštvorec, ktorý je rovnostranný, ale nie pravouhlý; kosodĺžnik, ktorý má opačné strany a uhly rovno navzájom, ale nie je ani rovnostranný, ani pravouhlý. Okrem týchto sú to štvoruholníky, ktoré sa nazývajú lichobežníky (rôznobežníky).
- Postulát 1: Nech je úlohou nakresliť priamku z ktoréhokoľvek bodu do ktoréhokoľvek bodu. Tento prvý postulát hovorí, že vzhľadom na akékoľvek dva body, ako sú A a B, existuje priamka AB, ktorá ich má ako koncové body. (Porovnaj s postulátom 5).
- Postulát 4: To, že všetky pravé uhly sa navzájom rovnajú.
- Tvrdenie 4: Ak dva trojuholníky majú dve strany rovnajúce sa dvom stranám a majú uhly obsiahnuté v rovnakých rovných priamkach rovnaké, potom majú tiež základňu rovnú základni, trojuholník sa rovná trojuholníku a zostávajúce uhly sa rovnajú zostávajúcim uhlom respektíve, a síce oproti rovnakým stranám. Veta o zhodnosti trojuholníkov - sus
- Tvrdenie 14: Ak na priamke a v bode na nej sú dve priamky, ktoré neležia na tej istej strane, sa súčet susedných uhlov rovná dvom pravým uhlom, potom sú tieto dve priamky navzájom k sebe v priamke (tvoria jednu priamku). Tvrdenie 31 Vytvor priamku cez daný bod rovnobežne s danou priamkou.
- Tvrdenie 41: Ak rovnobežník má rovnakú základňu s trojuholníkom a je medzi tými istými rovnobežkami, rovnobežník je dvakrát väčší ako trojuholník.
- Tvrdenie 46: Na danej priamke narysuj štvorec. (Súčasná matematická formulácia tejto vety: Nad danou úsečkou je možné narysovať štvorec.)
- Koncepcia/Zásada 2: Ak sú rovnosti pridané do rovnováhy, potom celky sú rovnaké.
- Koncepcia/Zásada 5: Celok je väčší než časť.
Cvičenie.
Vytvorte si vlastný applet, ktorým budete interpretovať Euklidov dôkaz Pytagorovej vety. Pozrite si náš návrh:
Vytvorte si vlastný applet, ktorým budete interpretovať Euklidov dôkaz Pytagorovej vety. Pozrite si náš návrh:
Veta (Euklidova veta o výške).
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony.
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony.
Dôkaz.
Nech v pravouhlom trojuholníku s pravým uhlom pri vrchole
s pravým uhlom pri vrchole  je
je 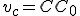 výška na preponu
výška na preponu 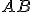 .
.
Zrejme platí:
Z podobnosti trojuholníkov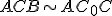 a
a 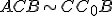 vyplýva:
vyplýva:
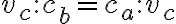 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 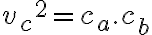 .
.
Tým je dôkaz Euklidovej vety o výške ukončený. Dôkaz, ktorý využíva zhodnosť od Vinklera nájdete Tu.
Nech v pravouhlom trojuholníku
 s pravým uhlom pri vrchole
s pravým uhlom pri vrchole  je
je 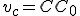 výška na preponu
výška na preponu  .
.
Zrejme platí:
- výška
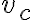 pravouhlého trojuholníka rozdelí trojuholník na ďalšie dva pravouhlé trojuholníky,
pravouhlého trojuholníka rozdelí trojuholník na ďalšie dva pravouhlé trojuholníky, - päta výšky
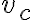 rozdelí preponu na dva úseky priľahlé k odvesnám trojuholníka:
rozdelí preponu na dva úseky priľahlé k odvesnám trojuholníka: 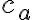 a
a 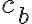 ,
, - zo vzťahu
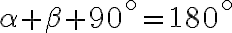 dostávame
dostávame 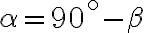 ,
, - všetky tri vzniknuté trojuholníky sú navzájom podobné:
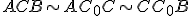 .
.
Z podobnosti trojuholníkov
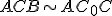 a
a 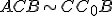 vyplýva:
vyplýva:
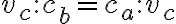 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 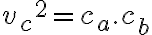 .
.
Tým je dôkaz Euklidovej vety o výške ukončený. Dôkaz, ktorý využíva zhodnosť od Vinklera nájdete Tu.
Veta (Euklidova veta o odvesne).
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a priľahlého úseku.
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a priľahlého úseku.
Dôkaz.
Z podobnosti trojuholníkov a
a 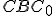 vyplýva:
vyplýva: 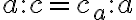 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 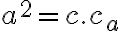 .
.
Z podobnosti trojuholníkov a
a 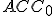 odvodíme druhú Euklidovu vetu
odvodíme druhú Euklidovu vetu 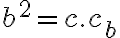 .
.
Z podobnosti trojuholníkov
 a
a 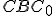 vyplýva:
vyplýva: 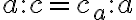 . Po úprave dostaneme vzťah
. Po úprave dostaneme vzťah 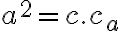 .
.
Z podobnosti trojuholníkov
 a
a 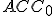 odvodíme druhú Euklidovu vetu
odvodíme druhú Euklidovu vetu 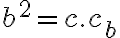 .
.
Cvičenie.
Dokážte Pytagorovu vetu pomocou Euklidových viet.
Dokážte Pytagorovu vetu pomocou Euklidových viet.
Zhodnosť a podobnosť trojuholníkov
Význam pojmov Zhodnosť a Podobnosť vo všeobecnosti možno vykladať rôznymi spôsobmi. V geometrii tieto termíny bežne sa používajú v prípadoch, ktoré sa týkajú merania. Prídavné meno zhodné (kongruentné) sa často používa na označenie predmetov, ktoré sa môžu prekrývať, zatiaľ čo podobné je voľnejšia myšlienka, ktorá spája predmety rovnakého charakteru.
- Fráza "zhodné objekty" sa používa na opis útvarov, ktoré za určitých okolností navzájom sa dajú premiestniť tak, aby "sa prekrývali". Charakteristika dvoch zhodných geometrických útvarov sa v matematike opiera o systém axióm. Zhodné útvary majú rovnaké rozmery a možno ich prekrývať, zatiaľ čo podobné útvary sú tie, ktoré sa zdajú byť identické, ale nemožno ich prekrývať. Obe tieto frázy môžu v širších súvislostiach označovať množstvo iných vecí.
- Termín "podobnosť" je odvodené z latinského slova "similis", čo znamená "ako alebo podobné". V matematickej oblasti si podobnosť vyžaduje dva objekty, ktoré majú rovnaký tvar, ale nie nevyhnutne rovnakú veľkosť.
Porovnávacia tabuľka prevzatá z UnAcademy
| Zhodný | Podobný | |
|---|---|---|
| Význam | Vzťahuje sa na postavy alebo čokoľvek iné, čo má rovnakú veľkosť a tvar a môže sa navzájom prekrývať. | Používa sa na opis postáv alebo iných objektov, ktoré majú podobnú veľkosť a tvar, ale nie sú identické z hľadiska rozmerov. |
| Presnosť | Geometricky "presné" a prekrývajúce sa útvary/obrazce sú známe ako zhodné útvary. | Slangová fráza pre identické postavy, ktoré majú veľa spoločného, pokiaľ ide o tvar ale nie veľkosť. |
| Orientácia | Dokonca aj keď sú umiestnené v opačných orientáciách, zhodné postavy sa navzájom prekrývajú. | Aj keď sú usporiadané v rovnakom smere, podobné objekty sa navzájom neprekrývajú. |
Definícia.
Vety o zhodnosti trojuholníkov
Veta (o zhodnosti trojuholníkoch).
- (sus) Trojuholníky, ktoré sa zhodujú v dvoch stranách a uhle nimi zovretom sú zhodné.
- (sss) Trojuholníky, ktoré sa zhodujú v troch stranách sú zhodné.
- (usu) Ak sa dva trojuholníky zhodujú v jednej strane a v dvoch uhloch priľahlých, tak sú zhodné.
- (Ssu) Ak sa dva trojuholníky zhodujú v dvoch stranách a v uhle oproti väčšej strane, tak sú zhodné.
Poznámka.
Uvedieme len dôkazy prvých dvoch viet tak, ako sú uvedené v Euklidových Základoch. Dôkazy viet (usu) a (Ssu) prenechávame čitateľovi ako cvičenie. Vyhľadajte v Základoch tieto vety a upravte Euklidove dôkazy tak, aby boli v súlade s modernou terminológiou.
Dôkaz.
Uvedieme len dôkazy prvých dvoch viet tak, ako sú uvedené v Euklidových Základoch. Dôkazy viet (usu) a (Ssu) prenechávame čitateľovi ako cvičenie. Vyhľadajte v Základoch tieto vety a upravte Euklidove dôkazy tak, aby boli v súlade s modernou terminológiou.
- Euklidových Základoch je veta sformulovaná ako
Proposition 4 (Euclid's Elements, Book I ).
- Nech
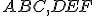 sú dva trojuholníky, ktoré majú dve strany
sú dva trojuholníky, ktoré majú dve strany 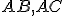 rovné dvom stranám
rovné dvom stranám 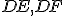 .
Konkrétne
.
Konkrétne 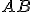 rovná
rovná 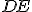 a
a 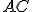 rovná
rovná 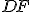 a uhol
a uhol 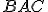 je rovný uhlu
je rovný uhlu 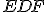 .
.
- Hovorím (Euklides), že základňa
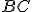 sa rovná aj základni
sa rovná aj základni 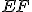 , trojuholník
, trojuholník  sa rovná
trojuholníku
sa rovná
trojuholníku 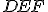 a zostávajúce uhly sa rovnajú zostávajúcim uhlom, respektíve opačne rovnakým stranám. To znamená, že
uhol
a zostávajúce uhly sa rovnajú zostávajúcim uhlom, respektíve opačne rovnakým stranám. To znamená, že
uhol  sa rovná uhlu
sa rovná uhlu 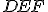 a uhol
a uhol  sa rovná uhlu
sa rovná uhlu 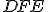 .
Nepriamy dôkaz
.
Nepriamy dôkaz
- Nech trojuholník
 je uložený na trojuholníku
je uložený na trojuholníku 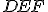 a ak je bod
a ak je bod  umiestnený na bode
umiestnený na bode
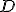 a priamka
a priamka 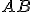 na
na 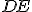 .
.
- Priamka
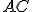 sa tiež rovná
sa tiež rovná 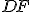 , pretože uhol
, pretože uhol 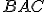 sa rovná uhlu
sa rovná uhlu 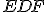 .
. - Ale
 sa tiež zhoduje s
sa tiež zhoduje s 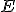 , a preto základňa
, a preto základňa 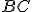 sa zhoduje so základňou
sa zhoduje so základňou 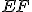 a rovná sa jej.
a rovná sa jej. - Takže celý trojuholník
 sa zhoduje s celým trojuholníkom
sa zhoduje s celým trojuholníkom 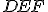 a rovná sa.
a rovná sa. - Zvyšné uhly sa zhodujú so zostávajúcimi uhlami a rovnajú sa, uhol
 sa rovná uhlu
sa rovná uhlu 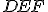 a uhol
a uhol 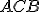 sa rovná uhlu
sa rovná uhlu 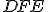 .
. -
Preto ak dva trojuholníky majú dve strany rovnobežné s dvoma stranami a majú uhly obsiahnuté rovnými čiarami rovnaké, potom majú aj základňu rovnú základni,
trojuholník sa rovná trojuholníku a zvyšné uhly sú rovné zvyšným uhlom respektíve tým, ktoré sú oproti rovnakým stranám.
Ilustračný obrázok vety (sus).
- Nech
- V Euklidových Základoch je veta sss sformulovaná ako Proposition 8 (Euclid's Elements, Book I ).
- Nech trojuholník
 je prenesený na trojuholník
je prenesený na trojuholník 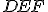 tak, aby bod
tak, aby bod  bol umiestnený na bode
bol umiestnený na bode 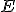 a priamka
a priamka 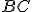 na
na 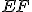 .
.
- Potom bod
 sa prekrýva (zhoduje) s bodom
sa prekrýva (zhoduje) s bodom 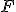 , pretože
, pretože 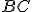 sa rovná
sa rovná 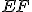 .
. - Ukážeme, že aj úsečka
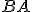 resp.
resp. 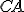 sa prekrýva (zhoduje) s úsečkou
sa prekrýva (zhoduje) s úsečkou 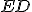 resp.
resp. 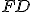 .
Budeme dokazovať nepriamo.
.
Budeme dokazovať nepriamo.
- Keďže trojuholník
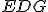 je rovnoramenný, tak uhol
je rovnoramenný, tak uhol 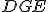 rovná uhlu
rovná uhlu 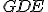 .
. - Z polohy bodu
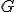 vyplýva, že uhol
vyplýva, že uhol
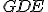 je väčší ako uhol
je väčší ako uhol 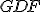 .
. - Tiež trojuholník
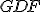 je rovnoramenný, preto aj uhol
je rovnoramenný, preto aj uhol 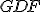 rovná uhlu
rovná uhlu 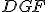 .
. - Z polohy bodu
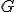 vyplýva, že uhol
vyplýva, že uhol 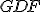 väčší ako uhol
väčší ako uhol 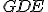 , čo je spor.
, čo je spor. - Preto musí byť bod
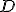 totožný s bodom
totožný s bodom 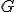 .
. - Podobne postupujeme v prípade, ak bod
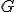 bude v polrovine
bude v polrovine 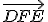 .
.
- Ukázali sme, že strana
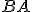 resp.
resp. 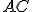 sa prekrýva so stranou
sa prekrýva so stranou 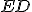 resp.
resp.
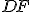 . To znamená, že uhol
. To znamená, že uhol 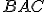 sa rovná uhlu
sa rovná uhlu 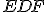 .
.
- Teraz stačí použiť vetu
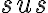 a dostávame tvrdenie: trojuholníky
a dostávame tvrdenie: trojuholníky  a
a 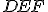 sú zhodné.
sú zhodné.
- Nech trojuholník
Vety o zhodnosti trojuholníkov sa využívajú hlavne v úlohách, v ktorých sa skúmajú a dokazujú špecifické vlastnosti geometrických útvarov. Uvedieme niekoľko takých úloh.
Príklad 1. (Veta sus)
Je daný obdĺžnik . Nech body
. Nech body  , sú bodmi uhlopriečky
, sú bodmi uhlopriečky 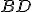 , pre ktoré platí
, pre ktoré platí 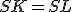 .
.
Dokážte, že trojuholníky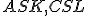 sú zhodné.
sú zhodné.
Je daný obdĺžnik
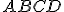 . Nech body
. Nech body 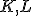 , sú bodmi uhlopriečky
, sú bodmi uhlopriečky 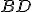 , pre ktoré platí
, pre ktoré platí 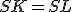 .
.
Dokážte, že trojuholníky
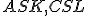 sú zhodné.
sú zhodné.
Ľahko sa presvedčíme, že trojuholníky 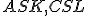 sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
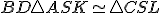 .
.
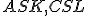 sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
sa zhodujú v dvoch stranách a v uhle nimi zovretom. Keďže
-
bod
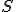 je stred uhlopriečky (uhlopriečky v obdĺžniku sa rozpoľujú)
je stred uhlopriečky (uhlopriečky v obdĺžniku sa rozpoľujú) - uhly
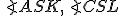 sú vrcholové, preto sú zhodné
sú vrcholové, preto sú zhodné
- úsečky
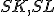 sú podľa predpokladu zhodné
sú podľa predpokladu zhodné
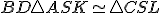 .
.
Príklad 2. (Veta sss)
Narysujte ľubovoľný rovnoramenný trojuholník so základňou
so základňou 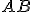 . Zostrojte stred
. Zostrojte stred  strany
strany
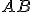 . Čo platí pre trojuholníky
. Čo platí pre trojuholníky 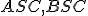 ? Ukážte, že platí
? Ukážte, že platí
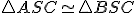 .
.
V trojuholníkoch Narysujte ľubovoľný rovnoramenný trojuholník
 so základňou
so základňou 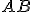 . Zostrojte stred
. Zostrojte stred  strany
strany
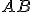 . Čo platí pre trojuholníky
. Čo platí pre trojuholníky 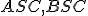 ? Ukážte, že platí
? Ukážte, že platí
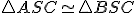 .
.
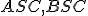 odpovedajúce strany majú rovnakú dĺžku. Keďže
odpovedajúce strany majú rovnakú dĺžku. Keďže
Poznámky.
- Tháles: V rovnoramennom trojuholníku uhly pri základni sú zhodné.
- Euklides: Základy/Proposition 5 (Euclid's Elements, Book I. )
Príklad 3. (Veta Ssu)
Na osi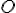 ostrého uhla
ostrého uhla 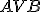 zostrojte vnútri uhla
zostrojte vnútri uhla 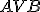 bod
bod 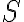 . Zostrojte kružnicu
. Zostrojte kružnicu 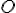
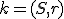 tak, aby platilo
tak, aby platilo 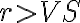 .
.
Označte priesečníky priamky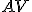 s kružnicou
s kružnicou  ako
ako 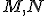 a priesečníky priamky
a priesečníky priamky
 s kružnicou
s kružnicou  ako
ako  .
.
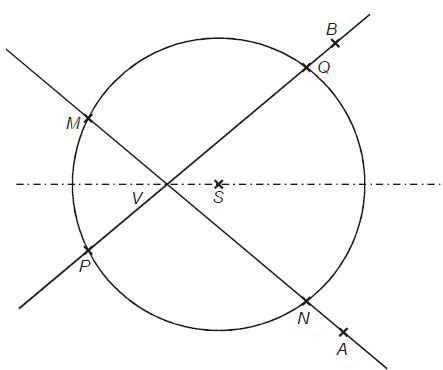
Dokážte, že úsečky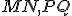 majú rovnakú veľkosť.
majú rovnakú veľkosť.
Na osi
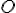 ostrého uhla
ostrého uhla 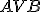 zostrojte vnútri uhla
zostrojte vnútri uhla 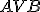 bod
bod 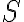 . Zostrojte kružnicu
. Zostrojte kružnicu 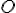
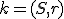 tak, aby platilo
tak, aby platilo 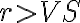 .
.
Označte priesečníky priamky
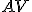 s kružnicou
s kružnicou  ako
ako 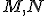 a priesečníky priamky
a priesečníky priamky
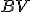 s kružnicou
s kružnicou  ako
ako 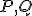 .
.
Dokážte, že úsečky
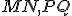 majú rovnakú veľkosť.
majú rovnakú veľkosť.
Analýza úlohy.
-
Najskôr sa pokúste dokázať rovnosť
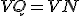 pomocou zhodnosti trojuholníkov:
pomocou zhodnosti trojuholníkov: 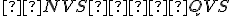 .
Pre tieto trojuholníky platí:
.
Pre tieto trojuholníky platí:
-
Potom dokážte rovnosť
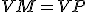 pomocou zhodnosti trojuholníkov:
pomocou zhodnosti trojuholníkov: 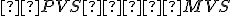 .
.
Pre tieto trojuholníky platí:- strana
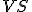 je spoločná obom trojuholníkom
je spoločná obom trojuholníkom -
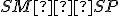 (polomery kružnice
(polomery kružnice  )
)
-
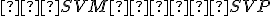 (súčet zhodných vrcholových uhlov a polovíc uhla
(súčet zhodných vrcholových uhlov a polovíc uhla 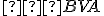 )
)
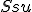 , preto aj tretie strany sú zhodné:
, preto aj tretie strany sú zhodné:
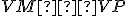
- strana
-
K ukončeniu dôkazu si stačí uvedomiť, že úsečky
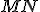 a
a 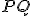 získame sčítaním dvoch dvojíc
zhodných úsečiek, platí
získame sčítaním dvoch dvojíc
zhodných úsečiek, platí 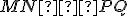 .
.
Záver. Trojuholníky sú zhodné podľa vety
 , preto aj tretie strany sú zhodné:
, preto aj tretie strany sú zhodné:
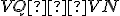 .
.
Príklad 4.
...
...
...
obr
Otvorte
...
Otvorte
Podobnosť
Definícia.
Dva trojuholníky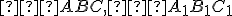 sú podobné, ak majú rovnaký pomer dĺžok odpovedajúcich si strán a odpovedajúce si uhly sú zhodné.
sú podobné, ak majú rovnaký pomer dĺžok odpovedajúcich si strán a odpovedajúce si uhly sú zhodné.
Dva trojuholníky
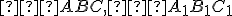 sú podobné, ak majú rovnaký pomer dĺžok odpovedajúcich si strán a odpovedajúce si uhly sú zhodné.
sú podobné, ak majú rovnaký pomer dĺžok odpovedajúcich si strán a odpovedajúce si uhly sú zhodné.
Trojuholník 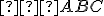 je podobný trojuholníku
je podobný trojuholníku 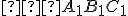 , práve vtedy keď existuje kladné číslo
, práve vtedy keď existuje kladné číslo
 také, že pre ich strany platí:
a pre ich uhly platí:
také, že pre ich strany platí:
a pre ich uhly platí:
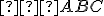 je podobný trojuholníku
je podobný trojuholníku 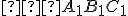 , práve vtedy keď existuje kladné číslo
, práve vtedy keď existuje kladné číslo
 také, že pre ich strany platí:
a pre ich uhly platí:
také, že pre ich strany platí:
a pre ich uhly platí:
Definícia.
Pomer nazývame koeficient podobnosti trojuholníkov.
Pre rôzne hodnoty koeficientu dostávame:
nazývame koeficient podobnosti trojuholníkov.
Pre rôzne hodnoty koeficientu dostávame:
Pomer
 nazývame koeficient podobnosti trojuholníkov.
Pre rôzne hodnoty koeficientu dostávame:
nazývame koeficient podobnosti trojuholníkov.
Pre rôzne hodnoty koeficientu dostávame:
Rozbor.
Uvažujme teraz o ľubovoľnom trojuholníku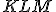 so stranami
so stranami 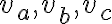 .
.
Dôkaz. Z rozboru a priamo z konštrukcie vyplýva, že pre výšky v zostrojenom trojuholníku platia vstupné hodnoty.
- Hľadajme súvislosti medzi výškami trojuholníka a jeho stranami. Použijeme vzťah pro obsah
trojuholníka:
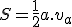 .
. - Z neho vyplýva, že
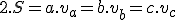 a teda
a teda 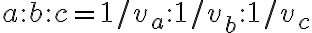 .
. - Označme
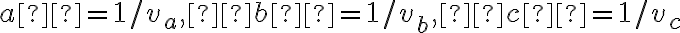
- Uvažujme o ľubovoľnom trojuholníku
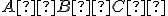 so stranami
so stranami 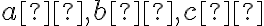 .
.
- Takýto trojuholník je podobný trojuholníku
 , lebo pomer odpovedajúcich strán je konštantný.
, lebo pomer odpovedajúcich strán je konštantný.
Uvažujme teraz o ľubovoľnom trojuholníku
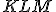 so stranami
so stranami 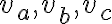 .
.
-
V trojuholníku
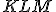 označme jeho výšky
označme jeho výšky 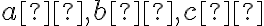 .
. - Zrejme platí:
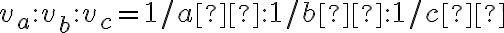 . Toto tvrdenie vyplýva z analýzy urobenej v druhom bode rozboru tejto úlohy.
. Toto tvrdenie vyplýva z analýzy urobenej v druhom bode rozboru tejto úlohy. - Po úprave dostaneme
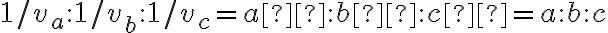 .
. - Konštrukciu začneme zostrojením trojuholníka
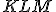 so stranami
so stranami 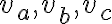
Dôkaz. Z rozboru a priamo z konštrukcie vyplýva, že pre výšky v zostrojenom trojuholníku platia vstupné hodnoty.
Cvičenie
- Zostrojte trojuholník
 , pre ktorý sú dané ťažnice
, pre ktorý sú dané ťažnice 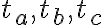 . Zadanie Tu.
. Zadanie Tu. -
Zostrojte trojuholník
 , pre ktorý je dané:
, pre ktorý je dané: 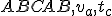 . Zadanie Tu.
Riešenie vyhľadajte v práci [DAV].
. Zadanie Tu.
Riešenie vyhľadajte v práci [DAV].
-
Zostrojte trojuholník
 , pre ktorý je daná výška
, pre ktorý je daná výška 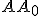 , ťažnica
, ťažnica 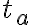 a stred opísanej kružnice
a stred opísanej kružnice  .
.
-
Daná je úsečka
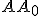 a priamka
a priamka  . Zostrojte trojuholník
. Zostrojte trojuholník  s vrcholom
s vrcholom  a výškou
a výškou
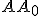 , ktorého ťažisko a stred kružnice opísanej ležia na priamke
, ktorého ťažisko a stred kružnice opísanej ležia na priamke  . Pozri 56. ročník MO, šk. rok 2006/2007, úloha B – I – 6.
. Pozri 56. ročník MO, šk. rok 2006/2007, úloha B – I – 6.
-
Zostrojte trojuholník
 , pre ktorý je daná výška
, pre ktorý je daná výška 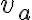 a ťažnice
a ťažnice 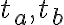 .
. - Zostrojte trojuholník
 , pre ktorý sú dané výšky
, pre ktorý sú dané výšky 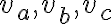 .
. -
Dokážte, že pre ťažnice
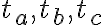 platí vzťah:
platí vzťah: 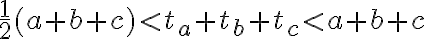 .Pozri prácu [KRI], str. 19.
.Pozri prácu [KRI], str. 19.
- Dokážte, že ťažnice v ľubovoľnom trojuholníku sa pretínajú v jednom bode pomocou osovej afinity.