Vektorový a afinný priestor
Analytické vyjadrenie
Rovnoľahlosť a posunutie
V tejto kapitole sa budeme zaoberať transformáciami euklidovskej roviny - posunutím a rovnoľahlosťou. Tieto zobrazenia v syntetickom poňatí geometrie definujeme
jednoducho pomocou
- pevne zvoleného vektora -posunutie,
- pevne zvoleného bodu a skalára - homotétia alebo tiež rovnoľahlosť. Ukážeme, že tieto zobrazenia sú afinné a určíme ich transformačné matice.
Dôkaz.
Rovnoľahlosť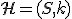 v euklidovskej rovine bodu
v euklidovskej rovine bodu 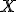 priraďuje bod
priraďuje bod 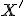 taký, že pre deliaci pomer bodov
taký, že pre deliaci pomer bodov 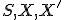 platí
platí 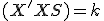 . Z definície deliaceho pomeru dostaneme vzťah
. Z definície deliaceho pomeru dostaneme vzťah
(h)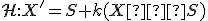 ,
,
kde![\small S[s_1,s_2] \in \mathbb E_2 \small S[s_1,s_2] \in \mathbb E_2](https://lms.umb.sk/filter/tex/pix.php/a1c26e689f4a4cb3e1f0d602a9905e22.png) je zvolený stred rovnoľahlosti a
je zvolený stred rovnoľahlosti a 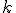 je reálny koeficient.
je reálny koeficient.
V prvom kroku musíme ukázať (dokázať), že obrazom troch kolineárnych bodov v rovnoľahlosti sú opäť tri kolineárne body. Najskôr dokážeme toto tvrdenie analyticky.
Nech![\small A[a_1,a_2],B[b_1,b_2],C[c_1,c_2] \small A[a_1,a_2],B[b_1,b_2],C[c_1,c_2]](https://lms.umb.sk/filter/tex/pix.php/69afe175d7ed037d38d7f0b09adfa934.png) sú ľubovoľné tri navzájom rôzne kolineárne body. Dvomi bodmi
sú ľubovoľné tri navzájom rôzne kolineárne body. Dvomi bodmi  je určená práve jediná priamka
je určená práve jediná priamka 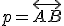 . Podľa predpokladu bod
. Podľa predpokladu bod 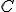 je bodom priamky
je bodom priamky 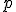 . V takom prípade existuje parameter
. V takom prípade existuje parameter 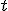 taký, že platia rovnosti
taký, že platia rovnosti
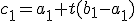 ,
,
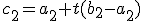 .
.
Označme![\small A'[a'_1,a'_2],B'[b'_1,b'_2],C'[c'_1,c'_2] \small A'[a'_1,a'_2],B'[b'_1,b'_2],C'[c'_1,c'_2]](https://lms.umb.sk/filter/tex/pix.php/6b451b3f2a1bcbe476b54b08ff273ea9.png) obrazy bodov
obrazy bodov 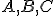 v rovnoľahlosti
v rovnoľahlosti 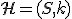 . Potom súradnice týchto bodov musia spĺňať vzťah (h), čo vedie k rovnostiam
. Potom súradnice týchto bodov musia spĺňať vzťah (h), čo vedie k rovnostiam
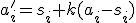
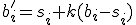
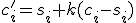
pre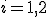 . Upravujme posledný výraz
. Upravujme posledný výraz
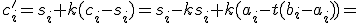
![\small =s_i-ks_i+ka_i-kt(b_i-a_i))= [𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖)]−𝑘𝑡(𝑏_𝑖−𝑠_𝑖−𝑎_𝑖+𝑠_𝑖)= \small =s_i-ks_i+ka_i-kt(b_i-a_i))= [𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖)]−𝑘𝑡(𝑏_𝑖−𝑠_𝑖−𝑎_𝑖+𝑠_𝑖)=](https://lms.umb.sk/filter/tex/pix.php/c681a01115932036b0e5d058fc3e367d.png)
![\small=𝑎′_𝑖−𝑘𝑡[(𝑏_𝑖−𝑠_𝑖)−(𝑎_𝑖−𝑠_𝑖)]= \small=𝑎′_𝑖−𝑘𝑡[(𝑏_𝑖−𝑠_𝑖)−(𝑎_𝑖−𝑠_𝑖)]=](https://lms.umb.sk/filter/tex/pix.php/52d68a8f94debc432367bf18d957ad68.png)
![\small=𝑎′_𝑖−𝑡[(𝑠_𝑖+𝑘(𝑏_𝑖−𝑠_𝑖))−(𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖))]= \small=𝑎′_𝑖−𝑡[(𝑠_𝑖+𝑘(𝑏_𝑖−𝑠_𝑖))−(𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖))]=](https://lms.umb.sk/filter/tex/pix.php/6b742adedf4d1e34816b71e1be573abd.png)
![\small=𝑎′_𝑖+𝑡[𝑏′_𝑖−𝑎′_𝑖] \small=𝑎′_𝑖+𝑡[𝑏′_𝑖−𝑎′_𝑖]](https://lms.umb.sk/filter/tex/pix.php/a95d131333c85242a71483af33b7ce7f.png) .
.
Dostali sme výraz, ktorý nám hovorí, že obraz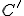 bodu
bodu 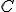 v zobrazení
v zobrazení 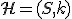 leží na priamke určenej
bodmi
leží na priamke určenej
bodmi 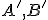 . Odkiaľ vyplýva, že zobrazenie
. Odkiaľ vyplýva, že zobrazenie 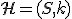 zachováva kolineárnosť a preto je afinným zobrazením.
zachováva kolineárnosť a preto je afinným zobrazením.
Syntetický (konštrukčný) dôkaz tvrdenia, že rovnoľahlosť zachováva kolineárnosť je pomerne jednoduchý. Stačí využiť vlastnosť, že v rovnoľahlosti sa rovnobežnosť zachováva. Pozrite si nasledujúci obrázok. Vlastnosť zachovania kolineárnosti vyplýva z podobnosti trojuholníkov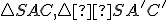 a
a 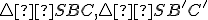 .
.
Rovnoľahlosť
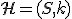 v euklidovskej rovine bodu
v euklidovskej rovine bodu 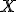 priraďuje bod
priraďuje bod 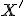 taký, že pre deliaci pomer bodov
taký, že pre deliaci pomer bodov 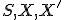 platí
platí 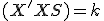 . Z definície deliaceho pomeru dostaneme vzťah
. Z definície deliaceho pomeru dostaneme vzťah(h)
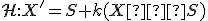 ,
,
kde
![\small S[s_1,s_2] \in \mathbb E_2 \small S[s_1,s_2] \in \mathbb E_2](https://lms.umb.sk/filter/tex/pix.php/a1c26e689f4a4cb3e1f0d602a9905e22.png) je zvolený stred rovnoľahlosti a
je zvolený stred rovnoľahlosti a 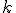 je reálny koeficient.
je reálny koeficient.
V prvom kroku musíme ukázať (dokázať), že obrazom troch kolineárnych bodov v rovnoľahlosti sú opäť tri kolineárne body. Najskôr dokážeme toto tvrdenie analyticky.
Nech
![\small A[a_1,a_2],B[b_1,b_2],C[c_1,c_2] \small A[a_1,a_2],B[b_1,b_2],C[c_1,c_2]](https://lms.umb.sk/filter/tex/pix.php/69afe175d7ed037d38d7f0b09adfa934.png) sú ľubovoľné tri navzájom rôzne kolineárne body. Dvomi bodmi
sú ľubovoľné tri navzájom rôzne kolineárne body. Dvomi bodmi  je určená práve jediná priamka
je určená práve jediná priamka 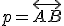 . Podľa predpokladu bod
. Podľa predpokladu bod 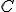 je bodom priamky
je bodom priamky 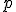 . V takom prípade existuje parameter
. V takom prípade existuje parameter 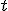 taký, že platia rovnosti
taký, že platia rovnosti
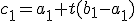 ,
,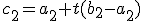 .
.Označme
![\small A'[a'_1,a'_2],B'[b'_1,b'_2],C'[c'_1,c'_2] \small A'[a'_1,a'_2],B'[b'_1,b'_2],C'[c'_1,c'_2]](https://lms.umb.sk/filter/tex/pix.php/6b451b3f2a1bcbe476b54b08ff273ea9.png) obrazy bodov
obrazy bodov 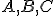 v rovnoľahlosti
v rovnoľahlosti 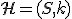 . Potom súradnice týchto bodov musia spĺňať vzťah (h), čo vedie k rovnostiam
. Potom súradnice týchto bodov musia spĺňať vzťah (h), čo vedie k rovnostiam
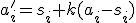
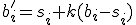
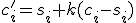
pre
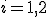 . Upravujme posledný výraz
. Upravujme posledný výraz
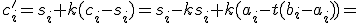
![\small =s_i-ks_i+ka_i-kt(b_i-a_i))= [𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖)]−𝑘𝑡(𝑏_𝑖−𝑠_𝑖−𝑎_𝑖+𝑠_𝑖)= \small =s_i-ks_i+ka_i-kt(b_i-a_i))= [𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖)]−𝑘𝑡(𝑏_𝑖−𝑠_𝑖−𝑎_𝑖+𝑠_𝑖)=](https://lms.umb.sk/filter/tex/pix.php/c681a01115932036b0e5d058fc3e367d.png)
![\small=𝑎′_𝑖−𝑘𝑡[(𝑏_𝑖−𝑠_𝑖)−(𝑎_𝑖−𝑠_𝑖)]= \small=𝑎′_𝑖−𝑘𝑡[(𝑏_𝑖−𝑠_𝑖)−(𝑎_𝑖−𝑠_𝑖)]=](https://lms.umb.sk/filter/tex/pix.php/52d68a8f94debc432367bf18d957ad68.png)
![\small=𝑎′_𝑖−𝑡[(𝑠_𝑖+𝑘(𝑏_𝑖−𝑠_𝑖))−(𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖))]= \small=𝑎′_𝑖−𝑡[(𝑠_𝑖+𝑘(𝑏_𝑖−𝑠_𝑖))−(𝑠_𝑖+𝑘(𝑎_𝑖−𝑠_𝑖))]=](https://lms.umb.sk/filter/tex/pix.php/6b742adedf4d1e34816b71e1be573abd.png)
![\small=𝑎′_𝑖+𝑡[𝑏′_𝑖−𝑎′_𝑖] \small=𝑎′_𝑖+𝑡[𝑏′_𝑖−𝑎′_𝑖]](https://lms.umb.sk/filter/tex/pix.php/a95d131333c85242a71483af33b7ce7f.png) .
.
Dostali sme výraz, ktorý nám hovorí, že obraz
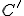 bodu
bodu 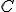 v zobrazení
v zobrazení 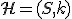 leží na priamke určenej
bodmi
leží na priamke určenej
bodmi 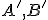 . Odkiaľ vyplýva, že zobrazenie
. Odkiaľ vyplýva, že zobrazenie 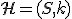 zachováva kolineárnosť a preto je afinným zobrazením.
zachováva kolineárnosť a preto je afinným zobrazením.
Syntetický (konštrukčný) dôkaz tvrdenia, že rovnoľahlosť zachováva kolineárnosť je pomerne jednoduchý. Stačí využiť vlastnosť, že v rovnoľahlosti sa rovnobežnosť zachováva. Pozrite si nasledujúci obrázok. Vlastnosť zachovania kolineárnosti vyplýva z podobnosti trojuholníkov
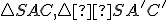 a
a 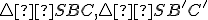 .
.
Vzťah (h) je vlastne parametrické vyjadrenie a predstavuje transformáciu roviny 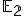 , ktorá bodu
, ktorá bodu ![\small X[x,y] \in \mathbb E_2 \small X[x,y] \in \mathbb E_2](https://lms.umb.sk/filter/tex/pix.php/e08e134049c7de5555f4ceb42445fae2.png) v rovnoľahlosti
v rovnoľahlosti 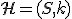 priradí bod
priradí bod
![\small X'[x',y'] \in \mathbb E_2 \small X'[x',y'] \in \mathbb E_2](https://lms.umb.sk/filter/tex/pix.php/95b6089b0fb9d1a688d01934e8311f0f.png) . Tento vzťah môžeme po jednoduchej úprave upraviť na sústavu dvoch rovníc o dvoch neznámych
. Tento vzťah môžeme po jednoduchej úprave upraviť na sústavu dvoch rovníc o dvoch neznámych 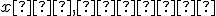
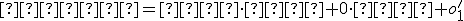
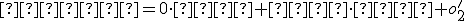 ,
,
kde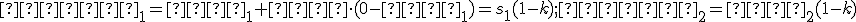 .
.
Usporiadaná dvojica![\small [s_1(1-k),𝑠_2(1-k)] \small [s_1(1-k),𝑠_2(1-k)]](https://lms.umb.sk/filter/tex/pix.php/2f077ed49890c27918ec06940cf36776.png) predstavuje súradnice obrazu počiatku
predstavuje súradnice obrazu počiatku ![\small O[0,0] \small O[0,0]](https://lms.umb.sk/filter/tex/pix.php/ab786f1f1348064c3558f8b3acc41e8c.png) v rovnoľahlosti
v rovnoľahlosti 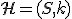 .
K dôkazu stačí dosadiť súradnice začiatku
.
K dôkazu stačí dosadiť súradnice začiatku ![\small O[0,0] \small O[0,0]](https://lms.umb.sk/filter/tex/pix.php/ab786f1f1348064c3558f8b3acc41e8c.png) do vzťahu (h).
do vzťahu (h).
Preskúmajme aké budú obrazy súradnicových ortonormálnych vektorov![\small \vec e_1=E_1-O=[1,0];\vec e_2=E_2-O=[0,1] \small \vec e_1=E_1-O=[1,0];\vec e_2=E_2-O=[0,1]](https://lms.umb.sk/filter/tex/pix.php/65697fba787ddf89773c3cd0e64c3e7b.png) v rovnoľahlosti
v rovnoľahlosti 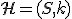 . Dosadením súradníc
bodov
. Dosadením súradníc
bodov 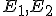 do vzťahu (h) dostaneme pre obrazy
do vzťahu (h) dostaneme pre obrazy 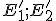
![\small E_1'=[k+s_1(1-k),s_2(1-k)],E_2'=[s_1(1-k),k+s_2(1-k)] \small E_1'=[k+s_1(1-k),s_2(1-k)],E_2'=[s_1(1-k),k+s_2(1-k)]](https://lms.umb.sk/filter/tex/pix.php/a57bd414561b5998b36d7af96b142cda.png) ,
,
po dosadení súradníc![\small O'[s_1(1-k),𝑠_2(1-k)] \small O'[s_1(1-k),𝑠_2(1-k)]](https://lms.umb.sk/filter/tex/pix.php/2d7c09fd2b900d768d74871f7bc77ed7.png) do rozdielov
do rozdielov 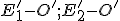 dostaneme súradnice obrazov
dostaneme súradnice obrazov 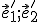
![\small \vec e_1'=([k+s_1(1-k)]-[s_1(1-k)],[s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(k,0)};\\ \small \vec e_2'=([s_1(1-k)]-[s_1(1-k)],[k+s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(0,k)} \small \vec e_1'=([k+s_1(1-k)]-[s_1(1-k)],[s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(k,0)};\\ \small \vec e_2'=([s_1(1-k)]-[s_1(1-k)],[k+s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(0,k)}](https://lms.umb.sk/filter/tex/pix.php/e7a44d83fd3a9987dbebea6aff9a1390.png)
Súradnice obrazov súradnicových ortonormálnych vektorov sú závisé len od koeficienta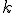 .
.
V súlade s definíciou analytického vyjadrenia afinného zobrazenia môžeme vyjadriť rovnoľahlosť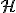 v rovine pomocou rozšíreného maticového tvaru takto:
v rovine pomocou rozšíreného maticového tvaru takto:
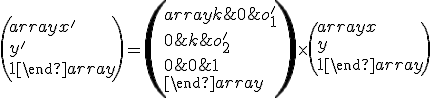 .
.
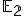 , ktorá bodu
, ktorá bodu ![\small X[x,y] \in \mathbb E_2 \small X[x,y] \in \mathbb E_2](https://lms.umb.sk/filter/tex/pix.php/e08e134049c7de5555f4ceb42445fae2.png) v rovnoľahlosti
v rovnoľahlosti 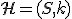 priradí bod
priradí bod
![\small X'[x',y'] \in \mathbb E_2 \small X'[x',y'] \in \mathbb E_2](https://lms.umb.sk/filter/tex/pix.php/95b6089b0fb9d1a688d01934e8311f0f.png) . Tento vzťah môžeme po jednoduchej úprave upraviť na sústavu dvoch rovníc o dvoch neznámych
. Tento vzťah môžeme po jednoduchej úprave upraviť na sústavu dvoch rovníc o dvoch neznámych 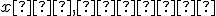
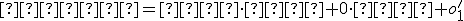
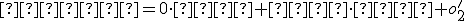 ,
,
kde
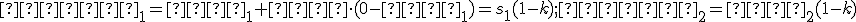 .
.
Usporiadaná dvojica
![\small [s_1(1-k),𝑠_2(1-k)] \small [s_1(1-k),𝑠_2(1-k)]](https://lms.umb.sk/filter/tex/pix.php/2f077ed49890c27918ec06940cf36776.png) predstavuje súradnice obrazu počiatku
predstavuje súradnice obrazu počiatku ![\small O[0,0] \small O[0,0]](https://lms.umb.sk/filter/tex/pix.php/ab786f1f1348064c3558f8b3acc41e8c.png) v rovnoľahlosti
v rovnoľahlosti 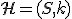 .
K dôkazu stačí dosadiť súradnice začiatku
.
K dôkazu stačí dosadiť súradnice začiatku ![\small O[0,0] \small O[0,0]](https://lms.umb.sk/filter/tex/pix.php/ab786f1f1348064c3558f8b3acc41e8c.png) do vzťahu (h).
do vzťahu (h).
Preskúmajme aké budú obrazy súradnicových ortonormálnych vektorov
![\small \vec e_1=E_1-O=[1,0];\vec e_2=E_2-O=[0,1] \small \vec e_1=E_1-O=[1,0];\vec e_2=E_2-O=[0,1]](https://lms.umb.sk/filter/tex/pix.php/65697fba787ddf89773c3cd0e64c3e7b.png) v rovnoľahlosti
v rovnoľahlosti 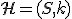 . Dosadením súradníc
bodov
. Dosadením súradníc
bodov 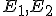 do vzťahu (h) dostaneme pre obrazy
do vzťahu (h) dostaneme pre obrazy 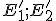
![\small E_1'=[k+s_1(1-k),s_2(1-k)],E_2'=[s_1(1-k),k+s_2(1-k)] \small E_1'=[k+s_1(1-k),s_2(1-k)],E_2'=[s_1(1-k),k+s_2(1-k)]](https://lms.umb.sk/filter/tex/pix.php/a57bd414561b5998b36d7af96b142cda.png) ,
,
po dosadení súradníc
![\small O'[s_1(1-k),𝑠_2(1-k)] \small O'[s_1(1-k),𝑠_2(1-k)]](https://lms.umb.sk/filter/tex/pix.php/2d7c09fd2b900d768d74871f7bc77ed7.png) do rozdielov
do rozdielov 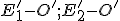 dostaneme súradnice obrazov
dostaneme súradnice obrazov 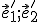
![\small \vec e_1'=([k+s_1(1-k)]-[s_1(1-k)],[s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(k,0)};\\ \small \vec e_2'=([s_1(1-k)]-[s_1(1-k)],[k+s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(0,k)} \small \vec e_1'=([k+s_1(1-k)]-[s_1(1-k)],[s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(k,0)};\\ \small \vec e_2'=([s_1(1-k)]-[s_1(1-k)],[k+s_2(1-k)]-[𝑠_2(1-k)])=\pmb{(0,k)}](https://lms.umb.sk/filter/tex/pix.php/e7a44d83fd3a9987dbebea6aff9a1390.png)
Súradnice obrazov súradnicových ortonormálnych vektorov sú závisé len od koeficienta
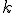 .
.
V súlade s definíciou analytického vyjadrenia afinného zobrazenia môžeme vyjadriť rovnoľahlosť
 v rovine pomocou rozšíreného maticového tvaru takto:
v rovine pomocou rozšíreného maticového tvaru takto:
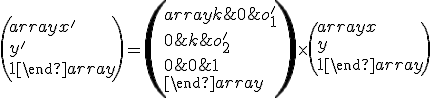 .
.
Poznámky.
- Maticu
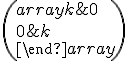 nazývame matica afinného zobrazenia (rovnoľahlosti), pričom prvky prvého (resp. druhého) stĺpca tejto matice predstavujú súradnice vektora
nazývame matica afinného zobrazenia (rovnoľahlosti), pričom prvky prvého (resp. druhého) stĺpca tejto matice predstavujú súradnice vektora 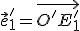 (resp. vektora
(resp. vektora 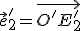 ), ktorý je obrazom vektora
), ktorý je obrazom vektora 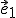 (resp. vektora
(resp. vektora 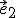 ) v danej rovnoľahlosti. V rovnoľahlosti rovnobežnosť sa zachováva, preto vektory
) v danej rovnoľahlosti. V rovnoľahlosti rovnobežnosť sa zachováva, preto vektory 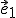 a
a 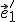 sú lineárne závislé, pričom
sú lineárne závislé, pričom 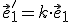 .
. - V transformačných rovniciach koeficienty pri neznámej
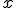 (resp.
(resp. 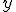 ) predstavujú súradnice vektora
) predstavujú súradnice vektora 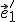 (resp. vektora
(resp. vektora 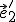 ).
).
Riešenie. Využite riešenie príkladu "Tri body" v kapitole "Afinné zobrazenie". Pozrite si grafické riešenie
Tu.
Úloha.
Vytvorte applet v GeoGebre, ktorý bude generovať transformačné rovnice pre posunutie v rovine.
Vytvorte applet v GeoGebre, ktorý bude generovať transformačné rovnice pre posunutie v rovine.
Pomoc. Inšpirujte sa appletom pre určenie transformačných rovníc posunutia v rovine pomocou programu GeoGebra. Návrh
Tu.
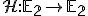
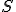
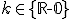
![\small A[-2,0] \rightarrow A'[-2,1],B[1,-1] \rightarrow B'[4,-1],C[-1,1] \rightarrow C'[0,3] \small A[-2,0] \rightarrow A'[-2,1],B[1,-1] \rightarrow B'[4,-1],C[-1,1] \rightarrow C'[0,3]](https://lms.umb.sk/filter/tex/pix.php/36c60da4c8ebc2dcdbeffef4aa2df2b6.png)
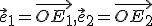
![\small E_1=[1,0],E_2=[0,1] \small E_1=[1,0],E_2=[0,1]](https://lms.umb.sk/filter/tex/pix.php/9348bdf47b8863f702b935e218adefe1.png)
