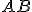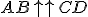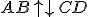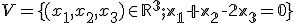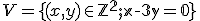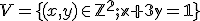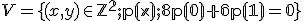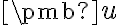Vektorový a afinný priestor
Vektorový priestor
Syntetický (geometrický) prístup
- Orientovaná úsečka je úsečka, ktorej krajné body majú určené poradie (pripúšťame aj nulovú orientovanú úsečku).
Ak
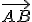 je orientovaná úsečka, bod
je orientovaná úsečka, bod 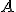 sa nazýva jej začiatočný bod, bod
sa nazýva jej začiatočný bod, bod 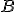 jej koncový bod.
jej koncový bod. - Hovoríme, že orientované úsečky
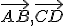 sú súhlasne orientované (rovnobežné, majú ten istý smer),
ak polpriamky
sú súhlasne orientované (rovnobežné, majú ten istý smer),
ak polpriamky 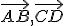 incidujú s priamkami tej istej osnovy a zároveň:
incidujú s priamkami tej istej osnovy a zároveň:
- Orientované úsečky
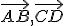 sú ekvivalentné ak stredy úsečiek
sú ekvivalentné ak stredy úsečiek 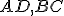 sú totožné.
sú totožné. - Množina všetkých orientovaných úsečiek ekvivalentných s
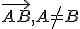 sa nazýva geometrický vektor.
sa nazýva geometrický vektor. - Orientovaná úsečka
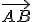 sa nazýva reprezentant (umiestnenie) vektora
sa nazýva reprezentant (umiestnenie) vektora 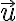 ,
zapisujeme
,
zapisujeme 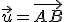 .
. - Geometrický vektor sa nazýva aj voľný vektor (množina všetkých orientovaných úsečiek) a konkrétna orientovaná úsečka sa nazýva viazaný vektor.
- Orientovaná úsečka
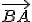 je reprezentuje opačný vektor k vektoru
je reprezentuje opačný vektor k vektoru 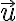 a označujeme ho
a označujeme ho 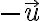 .
.
Cvičenie - [Mon 1.1.16 b]. Nezabudnite na nulové vektory.
Východiskové definície
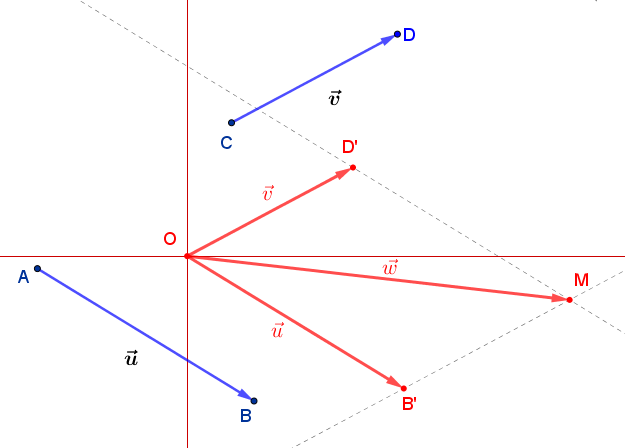
Vo všeobecnosti vektor je množina všetkých navzájom zhodných, súhlasne orientovaných úsečiek.
Umiestnením vektora sa nazýva každá orientovaná úsečka, ktorá tento vektor určuje. Umiestnením vektora do bodu sa nazýva také jeho umiestnenie, ktorého začiatočným bodom je daný bod.
Vektor určený orientovanou úsečkou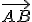 označíme tiež ako rozdiel bodov:
označíme tiež ako rozdiel bodov: 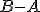 . Otvorte si applet
Tu.
. Otvorte si applet
Tu.
"Slovo vektor je prevzaté z latinského slova vector („nositeľ“, …). Vektor vznikol z potrieb fyziky (kde napr. vektor interpretujeme ako silu), do matematiky zaviedol vektory v r. 1853 írsky matematik a fyzik W. R. Hamilton (1805 – 1865). Takmer súčasnú podobu dal „vektorovému počtu“ na konci 19. storočia americký fyzik J. W. Gibbs (1839 – 1903)." Prevzaté z práce (Vranková).
Vo všeobecnosti vektor je množina všetkých navzájom zhodných, súhlasne orientovaných úsečiek.
Umiestnením vektora sa nazýva každá orientovaná úsečka, ktorá tento vektor určuje. Umiestnením vektora do bodu sa nazýva také jeho umiestnenie, ktorého začiatočným bodom je daný bod.
Vektor určený orientovanou úsečkou
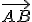 označíme tiež ako rozdiel bodov:
označíme tiež ako rozdiel bodov: 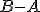 . Otvorte si applet
Tu.
. Otvorte si applet
Tu.
"Slovo vektor je prevzaté z latinského slova vector („nositeľ“, …). Vektor vznikol z potrieb fyziky (kde napr. vektor interpretujeme ako silu), do matematiky zaviedol vektory v r. 1853 írsky matematik a fyzik W. R. Hamilton (1805 – 1865). Takmer súčasnú podobu dal „vektorovému počtu“ na konci 19. storočia americký fyzik J. W. Gibbs (1839 – 1903)." Prevzaté z práce (Vranková).
Okruh 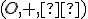 s jednotkou
s jednotkou 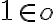
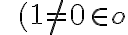 ), v ktorom každý nenulový prvok má vzhľadom na násobenie inverzný prvok, nazývame telesom.
Komutatívne teleso, v ktorom násobenie je komutatívna operácia, nazývame pole.
), v ktorom každý nenulový prvok má vzhľadom na násobenie inverzný prvok, nazývame telesom.
Komutatívne teleso, v ktorom násobenie je komutatívna operácia, nazývame pole.
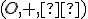 s jednotkou
s jednotkou 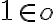
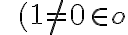 ), v ktorom každý nenulový prvok má vzhľadom na násobenie inverzný prvok, nazývame telesom.
Komutatívne teleso, v ktorom násobenie je komutatívna operácia, nazývame pole.
), v ktorom každý nenulový prvok má vzhľadom na násobenie inverzný prvok, nazývame telesom.
Komutatívne teleso, v ktorom násobenie je komutatívna operácia, nazývame pole.
Nech sú dané
• neprázdna množina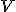 , ktorej prvky nazývame vektory,
, ktorej prvky nazývame vektory,
• pole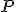 , ktorého prvky nazývame skaláry,
, ktorého prvky nazývame skaláry,
• zobrazenie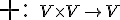 , ktoré nazývame sčítanie vektorov,
, ktoré nazývame sčítanie vektorov,
• zobrazenie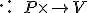 , ktoré nazývame násobenie vektora skalárom (prvkom z telesa
, ktoré nazývame násobenie vektora skalárom (prvkom z telesa 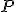 ).
).
• neprázdna množina
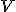 , ktorej prvky nazývame vektory,
, ktorej prvky nazývame vektory,
• pole
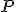 , ktorého prvky nazývame skaláry,
, ktorého prvky nazývame skaláry,
• zobrazenie
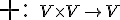 , ktoré nazývame sčítanie vektorov,
, ktoré nazývame sčítanie vektorov,
• zobrazenie
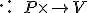 , ktoré nazývame násobenie vektora skalárom (prvkom z telesa
, ktoré nazývame násobenie vektora skalárom (prvkom z telesa 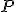 ).
).
Definícia.
Vektorový priestor nad poľom1)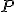 je množina
je množina 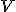 spolu s dvoma binárnymi operáciami (
spolu s dvoma binárnymi operáciami ( 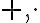 )
práve vtedy, keď súčasne platia vzťahy:
)
práve vtedy, keď súčasne platia vzťahy:
Vektorový priestor nad poľom1)
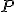 je množina
je množina 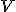 spolu s dvoma binárnymi operáciami (
spolu s dvoma binárnymi operáciami ( 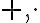 )
práve vtedy, keď súčasne platia vzťahy:
)
práve vtedy, keď súčasne platia vzťahy:
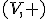 je abelovská grupa.
Vektorové axiómy
je abelovská grupa.
Vektorové axiómy
- asociatívnosť pre násobenie vektora skalárom:
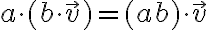
- invariancia vektora pri vynásobení jednotkovým prvkom poľa:
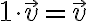 ,
,
kde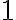 označuje multiplikatívnu identitu vo
označuje multiplikatívnu identitu vo 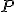
- distributívnosť (skalárneho) násobenia k sčítaniu vektorov:
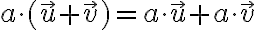
- distributívnosť násobenia vektora
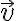 , ku sčítaniu skalárov
, ku sčítaniu skalárov  :
: 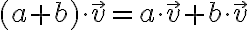
Na zopakovanie základných pojmov a vlastností algebraickej štruktúry "Vektorový priestor" odporúčame okrem práce od profesora Haviara aj e-knihu venovanú vektorovým priestorom od RNDr. Edity Vrankovej z Trnavskej univerzity v Trnave. Tiež na zopakovanie operácií s vektormi odporúčame prácu "Vektory v geometrii" od PaedDr. Miroslava Tisoňa, PhD., ktorá je dostupná
Tu.
Interpretujte vzťahy uvedené v definícii vektorového priestoru v prostredí GeoGebra!
Interpretujte vzťahy uvedené v definícii vektorového priestoru v prostredí GeoGebra!
Analytický (algebraický) prístup
Príklady vektorového priestoru
- Vektory v rovine so sčitovaním a násobením ako ho poznáte zo strednej školy, tvoria vektorový priestor nad telesom reálnych čísel
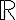 .
.
- Usporiadané
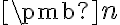 -tice reálnych čísel s operáciami
-tice reálnych čísel s operáciami 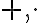 definovanými po súradniciach tvoria vektorový priestor
nad telesom reálnych čísel
definovanými po súradniciach tvoria vektorový priestor
nad telesom reálnych čísel 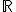 .
.
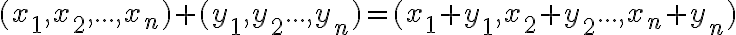
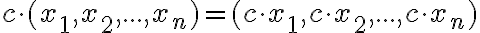
V ďalších častiach budeme prevažne pracovať s vektormi, ktoré tvoria usporiadané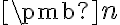 -tice reálnych čísel a to len pre rovinu
-tice reálnych čísel a to len pre rovinu 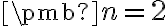 resp. priestor
resp. priestor 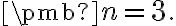
Ďalšie príklady vektorových priestorov sú množiny (všetkých)
- polynómov v jednej neurčitej nad poľom reálnych čísel, operácia - sčítanie polynómov "podľa rovnakých mocnín",
- reálnych funkcií, operácia - bežný súčet funkčných hodnôt,
- matíc typu
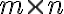 , operácia sčítania matíc - sčítanie v rovnakom riadku a stĺpci.
, operácia sčítania matíc - sčítanie v rovnakom riadku a stĺpci.
Cvičenie.
Nech je daná množina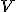 usporiadaných trojíc resp. dvojíc s obvyklým sčitovaním "po zložkách" trojíc resp. dvojíc reálnych čísel.
usporiadaných trojíc resp. dvojíc s obvyklým sčitovaním "po zložkách" trojíc resp. dvojíc reálnych čísel.
Nech je daná množina
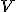 usporiadaných trojíc resp. dvojíc s obvyklým sčitovaním "po zložkách" trojíc resp. dvojíc reálnych čísel.
usporiadaných trojíc resp. dvojíc s obvyklým sčitovaním "po zložkách" trojíc resp. dvojíc reálnych čísel.
Riešenia.
- Uzavretosť operácie sčítania.
Pre ľubovoľné dva vektory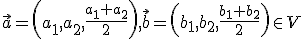 pre ich súčet platí
pre ich súčet platí
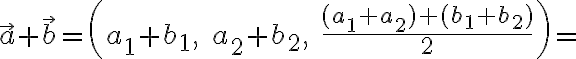
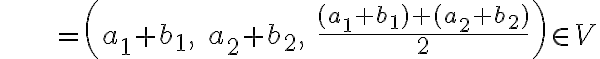 odkiaľ dostávame, že operácia + je uzavretá.
odkiaľ dostávame, že operácia + je uzavretá. - Postupujeme podobne ako v predchádzajúcom prípade.
- Operácia sčítania zrejme nie je uzavretá, lebo pre ľubovoľné dva vektory
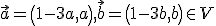
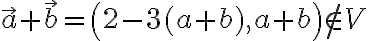 .
. -
Uvažujme dva ľubovoľné polynómy
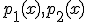 , ktoré sú prvkami množiny
, ktoré sú prvkami množiny 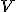 . Ďalej majme polynóm
. Ďalej majme polynóm 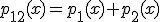 ,
ktorý je ich súčtom. Pre polynómy
,
ktorý je ich súčtom. Pre polynómy 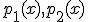 platí
platí
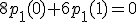 ,
,
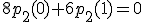 .
.
Sčítaním oboch rovníc získame![\small 8[p_1(0)+p_2(0)]+6[p_1(1)+p_2(1)]=0 \small 8[p_1(0)+p_2(0)]+6[p_1(1)+p_2(1)]=0](https://lms.umb.sk/filter/tex/pix.php/6140b7c4140309d2fa7b03be3821de1e.png) . Odkiaľ dostávame
. Odkiaľ dostávame
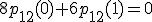 ,
,
teda že polynóm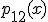 , čo je súčet ľubovoľných dvoch polynómov množiny
, čo je súčet ľubovoľných dvoch polynómov množiny 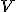 , je opäť prvkom tejto množiny.
Tým sme dokázali uzavretosť sčítania vektorov.
Pokúste sa o grafickú interpretáciu vektorov, ak budeme brať do úvahy iba polynómy 1. stupňa alebo len polynómy 2. stupňa. Viete určiť počiatočné a koncové body týchto vektorov? Otvorte so applet Tu.
, je opäť prvkom tejto množiny.
Tým sme dokázali uzavretosť sčítania vektorov.
Pokúste sa o grafickú interpretáciu vektorov, ak budeme brať do úvahy iba polynómy 1. stupňa alebo len polynómy 2. stupňa. Viete určiť počiatočné a koncové body týchto vektorov? Otvorte so applet Tu.
__________________________________________________________________________________________
1) Pole je teleso s komutatívnou multiplikatívnou operáciou .
.
2) Pozrite si stránku https://reseneulohy.cz/1356/vektorovy-prostor-ii
1) Pole je teleso s komutatívnou multiplikatívnou operáciou
 .
.
2) Pozrite si stránku https://reseneulohy.cz/1356/vektorovy-prostor-ii