Vedecké poznávanie vo vyučovaní matematiky
Problémy s mocninami s reálnym exponentom
Definícia (Mocnina s prirodzeným exponentom).
Pre každé reálne číslo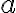 a prirodzené číslo
a prirodzené číslo  je:
Zápis
je:
Zápis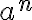 čítame "
čítame " -tá mocnina čísla
-tá mocnina čísla 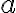 ". Číslo
". Číslo 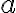 nazývame základ mocniny, číslo
nazývame základ mocniny, číslo  nazývame exponent .
nazývame exponent .
Pre každé reálne číslo
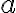 a prirodzené číslo
a prirodzené číslo  je:
Zápis
je:
Zápis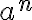 čítame "
čítame " -tá mocnina čísla
-tá mocnina čísla 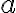 ". Číslo
". Číslo 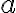 nazývame základ mocniny, číslo
nazývame základ mocniny, číslo  nazývame exponent .
nazývame exponent .
Cvičenie.
Pozrite si stránku Online kalkulačka rovníc, nerovníc a systémov.
Pozrite si stránku Online kalkulačka rovníc, nerovníc a systémov.
Vlastnosti.
-
Pre mocninu
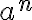 s exponentom
s exponentom 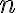 , ktorým je záporné celé číslo platí: ( a^n= \frac{1}{a^ {-n}} \).
, ktorým je záporné celé číslo platí: ( a^n= \frac{1}{a^ {-n}} \). -
Nech
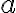 je kladné reálne číslo a nech
je kladné reálne číslo a nech 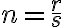 je racionálny exponent, kde
je racionálny exponent, kde  je celé číslo a
je celé číslo a 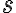 je kladné celé číslo.
Potom je možné robiť úpravy typu
je kladné celé číslo.
Potom je možné robiť úpravy typu
-
Pre
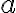 záporné reálne číslo a racionálny exponent
záporné reálne číslo a racionálny exponent 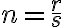 , nie je možné použiť predchádzajúcu úpravu. Pozri cvičenie 2.
, nie je možné použiť predchádzajúcu úpravu. Pozri cvičenie 2.
Definícia (Binomická rovnica).
Binomická rovnica s neznámou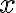 je rovnica v tvare
je rovnica v tvare 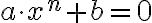 , kde
, kde 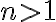 je prirodzené číslo a
je prirodzené číslo a 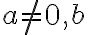 sú komplexné čísla.
sú komplexné čísla.
Binomická rovnica s neznámou
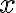 je rovnica v tvare
je rovnica v tvare 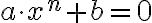 , kde
, kde 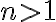 je prirodzené číslo a
je prirodzené číslo a 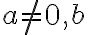 sú komplexné čísla.
sú komplexné čísla.
Základná veta algebry hovorí, že každý polynóm stupňa aspoň prvého s komplexnými koeficientami má v telese komplexných čísel aspoň jeden koreň.
Diskusia k riešeniu binomických rovníc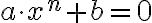 .
.
Zo základnej vety algebry vyplýva, že táto rovnica má práve riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
Každú binomickú rovnicu môžeme upraviť na normovaný tvar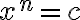 . My sa budeme venovať len binomickým rovniciam, v ktorých
. My sa budeme venovať len binomickým rovniciam, v ktorých 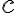 je reálne číslo. Naviac sa zameriame na riešenie rovníc
je reálne číslo. Naviac sa zameriame na riešenie rovníc 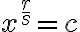 , v ktorých exponent
, v ktorých exponent 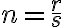 je racionálne číslo.
V tomto prípade rovnicu
je racionálne číslo.
V tomto prípade rovnicu 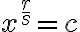 najskôr transformujeme na normovaný tvar
najskôr transformujeme na normovaný tvar 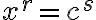 . Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
. Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
Diskusia k riešeniu binomických rovníc
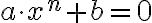 .
.
Zo základnej vety algebry vyplýva, že táto rovnica má práve
 riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
riešení v obore komplexných čísel (medzi nimi môžu byť aj násobné korene).
Každú binomickú rovnicu môžeme upraviť na normovaný tvar
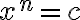 . My sa budeme venovať len binomickým rovniciam, v ktorých
. My sa budeme venovať len binomickým rovniciam, v ktorých 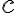 je reálne číslo. Naviac sa zameriame na riešenie rovníc
je reálne číslo. Naviac sa zameriame na riešenie rovníc 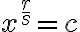 , v ktorých exponent
, v ktorých exponent 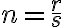 je racionálne číslo.
V tomto prípade rovnicu
je racionálne číslo.
V tomto prípade rovnicu 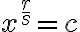 najskôr transformujeme na normovaný tvar
najskôr transformujeme na normovaný tvar 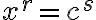 . Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
. Takáto transformácia nie je ekvivalentnou
úpravou, preto je v závere nutné urobiť skúšku správnosti riešenia. O riešení binomických rovníc odporúčame prácu "Komplexní čísla", ktorá je dostupná
Tu.
K praktickému riešeniu môžete využiť online kalkulačku rovníc "MathDF" dostupnú Tu.
- Riešenie prvej rovnice
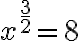 z prvého cvičenia po transformácii na
z prvého cvičenia po transformácii na 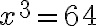 s využitím online kalkulačky:
s využitím online kalkulačky:
 .
. - Riešením druhej rovnice
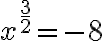 z prvého cvičenia po transformácii na
z prvého cvičenia po transformácii na 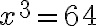
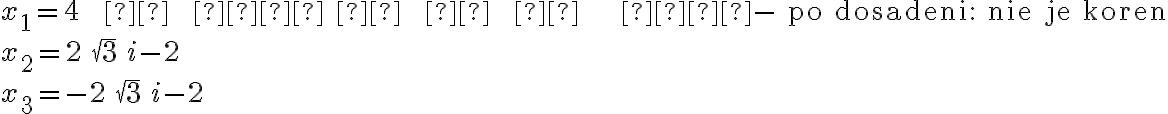
Cvičenie.
Vyriešte rovnicu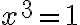 v obore komplexných čísel.
v obore komplexných čísel.
Návod:
Vyjadrite hľadané riešenie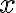 v goniometrickom tvare
v goniometrickom tvare 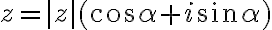 alebo použite vzťah
alebo použite vzťah
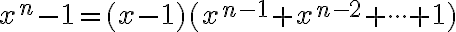 .
.
Vyriešte rovnicu
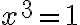 v obore komplexných čísel.
v obore komplexných čísel.
Návod:
Vyjadrite hľadané riešenie
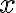 v goniometrickom tvare
v goniometrickom tvare 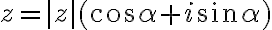 alebo použite vzťah
alebo použite vzťah
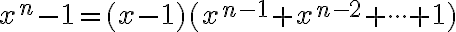 .
.
Pri definovaní pojmu reálne číslo vychádzame z existujúcej množiny racionálnych čísel, ale rozšírenie neurobíme pomocou karteziánskeho súčinu.
Konštrukcia, ktorá "zostrojí" reálne číslo, bude vychádzať z "rezov" na množine racionálnych čísel. Pozrite si kurz Aritmetika Tu.
Konštrukcia, ktorá "zostrojí" reálne číslo, bude vychádzať z "rezov" na množine racionálnych čísel. Pozrite si kurz Aritmetika Tu.
- Termín reálne číslo zaviedol René Descartes (1637) ako spoločný názov pre racionálne a iracionálne čísla.
-
Viac ako dve tisíc rokov sú známe niektoré iracionálne čísla, ktoré sú vyjadrené ako odmocniny (mocniny s racionálnym exponentom) prirodzených čísel
![\sqrt {2}, \sqrt[3]{2} \sqrt {2}, \sqrt[3]{2}](https://lms.umb.sk/filter/tex/pix.php/6d5c677fe326c298cf44e745f38c7e46.png) ...
... -
Euler (1737) dokázal, že číslo
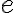 je
iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
je
iracionálne a Lambert ((1768) dokázal, že Ludolfovo číslo
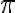 je iracionálne.
je iracionálne. - Charles Hermit (1873) ukázal, že číslo
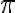 je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami.
je transcendentné - nie je riešením algebraickej rovnice s celočíselnými koeficientami.
Poznámky.
-
Zo strednej školy si možno pamätáte, že
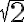 má nekonečný a neperiodický dekadický rozvoj.
má nekonečný a neperiodický dekadický rozvoj. - dokonca niektorí si pamätajú aj niekoľko cifier za desatinnou čiarkou, napr.
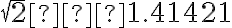
- na stránke Wikipédie môžeme nájsť až 10 miliónov cifier
- vyjadriť
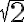 konečným počtom cifier sa nikomu nemôže podariť
konečným počtom cifier sa nikomu nemôže podariť - existuje racionálne číslo, ktoré aproximuje
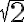 s danou presnosťou.
s danou presnosťou. - Vieme nájsť vhodnú postupnosť racionálnych čísel, ktorej členy sa budú „približovať“ k druhej odmocnine z dvoch.
- Ak vezmeme do úvahy všetky možné konvergentné postupnosti racionálnych čísel, tak ich limity budú zahŕňať aj čísla typu
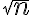 .
. - V nasledujúcich kapitolách popíšeme Dedekindove rezy, pomocou ktorých definujeme reálne čísla.
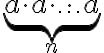
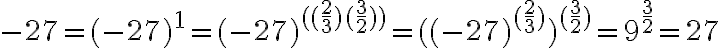
![a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r](https://lms.umb.sk/filter/tex/pix.php/3e7b97dda331b0af77ba047a99702a02.png)