Zhodné a podobné zobrazenia - cvičenia
Cvičenie
Cvičenie - osová súmernosť
Je daná priamka a body
a body 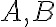 ležiace v tej istej polrovine s hraničnou priamkou
ležiace v tej istej polrovine s hraničnou priamkou  . Určte bod
. Určte bod
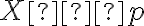 tak, aby súčet
tak, aby súčet
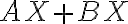 bol čo najmenší.
bol čo najmenší.
Riešenie Tu
Je daná priamka
 a body
a body 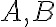 ležiace v tej istej polrovine s hraničnou priamkou
ležiace v tej istej polrovine s hraničnou priamkou  . Určte bod
. Určte bod
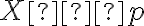 tak, aby súčet
tak, aby súčet
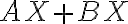 bol čo najmenší.
bol čo najmenší.
Riešenie Tu
Cvičenie - stredová súmernosť.
Sú dané dve sústredné kružnice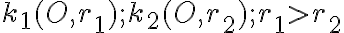 . A bod
. A bod
 vo vnútri
vo vnútri 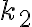 . Zostrojte obdĺžnik
. Zostrojte obdĺžnik
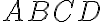 tak, že
tak, že 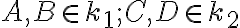 a bod
a bod
 je jeho stredom. Riešenie Tu.
je jeho stredom. Riešenie Tu.
Sú dané dve sústredné kružnice
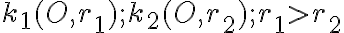 . A bod
. A bod
 vo vnútri
vo vnútri 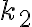 . Zostrojte obdĺžnik
. Zostrojte obdĺžnik
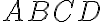 tak, že
tak, že 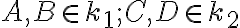 a bod
a bod
 je jeho stredom. Riešenie Tu.
je jeho stredom. Riešenie Tu.
Cvičenie - posunutie
Zostrojte rovnobežník ak sú dané veľkosti jeho strán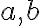 a veľkosť
a veľkosť 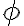 uhla, ktorý zvierajú jeho uhlopriečky. Zadanie Tu
uhla, ktorý zvierajú jeho uhlopriečky. Zadanie Tu
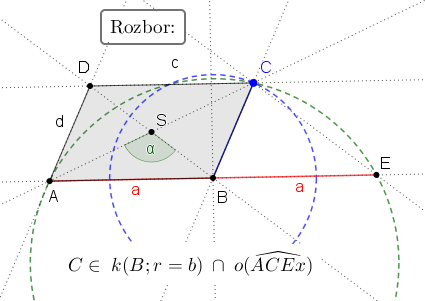
Zostrojte rovnobežník ak sú dané veľkosti jeho strán
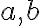 a veľkosť
a veľkosť 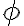 uhla, ktorý zvierajú jeho uhlopriečky. Zadanie Tu
uhla, ktorý zvierajú jeho uhlopriečky. Zadanie Tu
Cvičenie - posunutá súmernosť
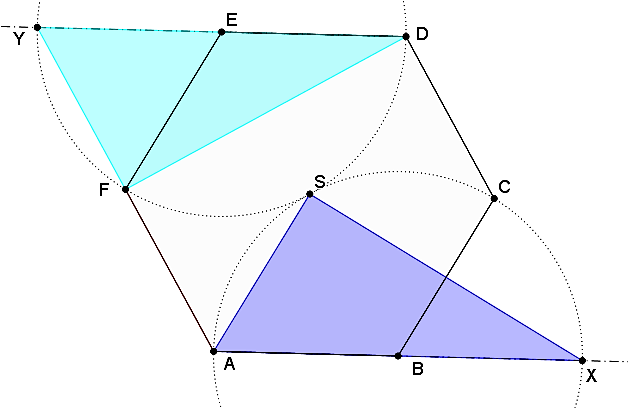
Daný je pravidelný 6-uholník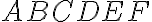 a body
a body
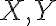 , pričom
, pričom
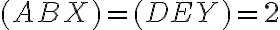 . Nájdite zhodné zobrazenie, ktoré zobrazí trojuholník
. Nájdite zhodné zobrazenie, ktoré zobrazí trojuholník
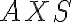 do trojuholníka
do trojuholníka
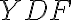 .
Bude to priama alebo nepriama zhodnosť?
.
Bude to priama alebo nepriama zhodnosť?
Riešenie
 Otvorte si applet Tu.
Otvorte si applet Tu.
Daný je pravidelný 6-uholník
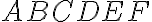 a body
a body
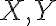 , pričom
, pričom
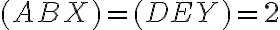 . Nájdite zhodné zobrazenie, ktoré zobrazí trojuholník
. Nájdite zhodné zobrazenie, ktoré zobrazí trojuholník
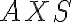 do trojuholníka
do trojuholníka
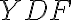 .
Bude to priama alebo nepriama zhodnosť?
.
Bude to priama alebo nepriama zhodnosť?
Riešenie
Cvičenie - rovnoľahlosť
Sú dané dva rôzne body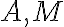 , ktorých vzdialenosť je
, ktorých vzdialenosť je 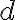 . Ďalej je dané kladné číslo
. Ďalej je dané kladné číslo 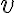 . Zostrojte kosoštvorec
. Zostrojte kosoštvorec
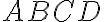 s výškou
s výškou 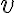 tak ,aby bod
tak ,aby bod
 bol stredom jeho strany
bol stredom jeho strany
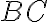 .
.
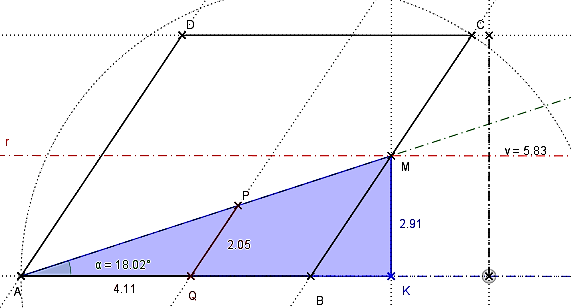 (rozbor)
(rozbor)
Riešenie. Križalkovič, K.: 500 riešených úloh z geometrie. Prík. 103.
Sú dané dva rôzne body
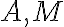 , ktorých vzdialenosť je
, ktorých vzdialenosť je 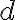 . Ďalej je dané kladné číslo
. Ďalej je dané kladné číslo 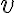 . Zostrojte kosoštvorec
. Zostrojte kosoštvorec
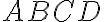 s výškou
s výškou 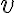 tak ,aby bod
tak ,aby bod
 bol stredom jeho strany
bol stredom jeho strany
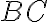 .
.
Riešenie. Križalkovič, K.: 500 riešených úloh z geometrie. Prík. 103.
