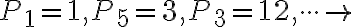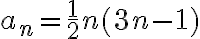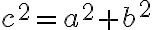Grécka matematika
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Dejiny matematiky |
| Kniha: | Grécka matematika |
| Vytlačil(a): | Visiteur anonyme |
| Dátum: | streda, 3 júla 2024, 12:27 |
Vedecká podstata
Matematika ako veda vznikla v Grécku približne v období 6. - 5. st. pred n. l.
- Bol vytvorený systém základných vzťahov (axióm) a požiadaviek (postulátov)
- Matematika sa stáva deduktívnou vedou
- Začali matematické tvrdenia dokazovať
Gréci ako prví prestali riešiť iba otázku ako, ale hľadali aj odpovede na otázku prečo.
- Používali desiatkový systém, ktorý ale nebol pozičný
- Gréci mali usporiadaný systém poznatkov o geometrii
- Riešili tri preslávené problémy:
- trisekcia uhla (rozdelenie uhla na tri rovnaké uhly)
- zdvojenie kocky (nájdenie kocky, ktorej objem sa rovná dvojnásobku kocky pôvodné)
- kvadratúru kruhu (nájdenie štvorca, ktorý má rovnaký obsah ako daný kruh).
- Vypracujte seminárnu prácu na tému "Zaujímavosti z gréckej matematiky. Použite prácu JAROSLAV FOLTA: DĚJINY MATEMATIKY I
Tháles z Milétu
Tháles (* cca 624 pred Kr. – † cca 546 pred Kr.)
 [Famous Mathematicians]
[Famous Mathematicians]
Je považovaný za prvého gréckeho filozofa, za jedného zo siedmich mudrcov.
- V Egypte nadobudol matematické znalosti, vypočítal výšku pyramíd podľa dĺžky ich tieňov
- Pripisujú sa mu dôkazy prvých geometrických viet
- Predpovedal zatmenie Slnka v r 585 pred Kr.
- Grécka matematika sa od tohto momentu vyvíjala nezvyčajne rýchlym tempom
- S jeho menom sa spája príbeh o tom, ako zbohatol predpovedaním počasia počas zberu olív.
- Thales sa tiež zapojil do politických záležitostí obrany Anatólijcov proti Perzii.
- Vypočítal tiež rovnodennosti a slnovraty za rok.
V geometrii je mu pripisovaná formulácia najjednoduchších planimetrických poučiek
- Priemer delí kruh na dve polovice
- Uhly pri základni rovnoramenného trojuholníka sú zhodné
- Ak sa dve priamky pretínajú, tak protiľahlé vrcholové uhly sú zhodné
- Všetky uhly nad priemerom sú pravé (tzv. Thálesova veta)
- Dva trojuholníky sú zhodné, ak sa zhodujú v dvoch uhloch a strane
Výška pyramídy
Tháles a podobnosť trojuholníkov
- Táles sa pousmial: Zmeriam výšku pyramídy.
- Kňaz sa nedôverčivo spýtal: Ako?
- Ak bude môj tieň práve taký dlhý ako je moja telesná výška, tak v tom okamihu musí merať dĺžka tieňa pyramídy práve toľko, ako je vysoká pyramída.
Jednoduchosť riešenia skrývala matematickú podstatu podobnosti trojuholníkov
Pytagoras zo Samos
Pytagoras(* cca 569 pred Kr. – † cca 475 pred Kr.)

Pytagoras bol politik, filozof, mysliteľ a matematik.
- Pytagorova škola mala charakter náboženskej školy či sekty
- Z Krotónu boli Pytagorejci vyhnaní
- Pytagoras snáď zomrel v Metapontu
Pytagoras zohral dôležitú úlohu vo vývoji matematiky, žiaľ vieme pomerne málo o jeho matematických úspechoch.
- Na Pytagora mal významný vplyv Tháles.
- Pytagoras navštívil Thálesa v Milétu, keď mal asi 20 rokov a Táles bol už starý muž.
- Na odporúčanie Tálesa Pytagoras navštívil Egypt, kde si prehĺbil vedomosti z geometrie.
- V roku 525 pred Kr. Pytagoras bol po Perzskej vojne s Egyptom zajatý a prevezený do Babylonu.
- V Babylone mal možnosť zoznámiť sa s rozvinutou babylonskou aritmetikou.
- Približne 520 rokov pred naším letopočtom Pytagoras sa vrátil do Samos.
Pytagorova škola
Grécku matematiku podstatne ovplyvnila Pytagorova škola


V Raphaelovej freske The School of Athens je Pythagoras zobrazený ako mladý muž.
Pytagorejci presadzovali štúdium kvadrivia - geometrie, aritmetiky, astronómie a hudby.
Pytagorejci číslo 1 považovali za základný stavebný kameň aritmetiky
- Tvrdili, že číslo 1 pochádza priamo od Boha ako základ všetkých ďalších čísel.
- Presadzovali mystiku čísel: "veci sú čísla".
- Prirodzené čísla 2, 3, 4, 5, ... boli chápané ako súhrny jednotiek.
- Kladné racionálne čísla boli predstavované pomocou pomerov prirodzených čísel.
Pytagorejci zaviedli čistú matematickú abstrakciu a zovšeobecnenie
Magickým obrazcom pre Pytagorejcov bol pravidelný päťuholník, v ktorom sa uhlopriečky rozdeľujú v pomere zlatého rezu.
Jeho konštrukcia pomocou pravítka a kružidla bola obrovským úspechom vtedajšej
geometrie.
Harmónia čísel
Jednotlivé čísla mali podľa Pytagorejcov osobitný význam a moc
- Čo je najmúdrejšie? - Číslo a potom ten, kto dal veciam mená.
- Čo je najkrajšie? - Harmónia.
- Čo je najmocnejšie? - Myšlienka. ... Číslu sa podobá všetko 2).
Pytagorejci si vytvorili niekoľko kategórií čísel:
-
Párne čísla boli ženské
-
Nepárne mužské
-
Číslo 4 predstavovalo spravodlivosť: 2 + 2 = 2 x 2
-
Číslo 10 predstavovalo dokonalosť: 1 + 2 + 3 + 4 = 10
Číslo 1 predstavuje základnú jednotku, ale aj bod, číslo 2 predstavuje základnú jednotku párnych čísel, ale aj to, že dva rôzne body určujú priamku, číslo 3 predstavuje trojuholník, ale aj to, že tri body mimo rámca v priamke určujú rovinu, číslo 4 predstavuje štvorsten, ale aj to, že štyri body mimo rámca v rovine reprezentujú priestor.
2) Zlomky předsokratovských myslitelů, ČSAV, Praha 1962, str. 40-41
Figurálne čísla
Na znázornenie figurálnych čísel používali hromádku kamenia, ktoré zoskupovali do geometrických útvarov
Tento geometrický jazyk im umožňoval dokázať tvrdenia, ktoré dnes väčšinou zapisujeme algebricky.
- Súčet dvoch (ne)párnych čísel je číslo párne
-
- Súčet párneho a nepárneho čísla je číslo párne
-
Dokážte takouto metódou, že súčet dvoch po sebe idúcich trojuholníkových čísel je číslo štvorcové.
Pytagorova veta
Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
Pytagorova veta je pomenovaná podľa starogréckeho matematika Pytagora, ktorý ju odvodil v 6. storočí pred Kr.
- Dôkazov Pytagorovej vety existuje veľmi veľa, viac ako 300, pozri na GeoGebre Tu.
- Vyhľadajte pôvodný Euklidov dôkaz v Knihe I, tvrdenie T/XLVII)
- Pozrite si dôkaz Pytagorovej vety v programe GeoGebra, ktorý vychádza z Euklidovho dôkazu. Otvorte si applet Tu →
- Iné dôkazy Pytagorovej vety nájdeme na stránke M. Viklera alebo Wikipedia.
- Dôkaz "bez slov" →. Doplňte "slová" pre tento dôkaz - urobte slovné/písomné zdôvodnenie.
- Pytagorova veta pravdepodobne bola známa aj v iných starovekých civilizáciách, napríklad v Číne, Egypte.
- Starí Egypťania stavali pozoruhodné stavby, pri ktorých potrebovali vytyčovať aj pravé uhly. Robili to takto:
- na špagáte uviazali rovnomerne 12 uzlov,
- prvý a posledný uzol upevnili na tom istom mieste - A a štvrtý na mieste C a siedmy na B,
- vznikol pravý uhol ACB.
Dané sú sústredné kružnice
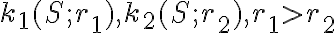 . Určte vzťah medzi obsahom
medzikružia ohraničeného kružnicami
. Určte vzťah medzi obsahom
medzikružia ohraničeného kružnicami 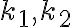 a obsahom kruhu nad tetivou
a obsahom kruhu nad tetivou 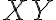 kružnice
kružnice
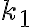 , ktorá sa dotýka kružnice
, ktorá sa dotýka kružnice 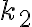 . Riešenie
. RiešeniePreskúmajte súvislosť tejto úlohy s dôkazom Pytagorovej vety aplikáciou Mamikonovej vety1). Otvorte si applet Tu.
1) Mamikonova veta →
Euklides z Alexandrie

Euklidov život
O Euklidovom živote vieme veľmi málo.
Pravdepodobne sa narodil v Aténach okolo roku 340 pre n. l. Patril k žiakom filozofa Platóna.
Okolo roku 300 pred n. l. zhrnul vtedajšie geometrické poznatky, obohatil ich vlastnými matematickými výsledkami a usporiadal do znamenitého diela Stoicheia – Základy. Táto práca sa stala jedinou učebnicou matematiky na celé stáročia.
Základy - Stocheia
V Základoch sú vysvetlené základy planimetrie, stereometrie a geometrickej algebry.
- Každá kniha sa začína definovaním – objasnením, názorným popisom všetkých geometrických objektov.
- Za nimi nasledujú postuláty – konkrétne vlastnosti geometrických útvarov i axiómy – výpovede o vlastnostiach negeometrických veličín.
- Potom sú uvedené matematické vety. s dôkazmi a so všetkými odkazmi na predchádzajúce vety, postuláty a axiómy.
Dielo Základy sa skladá z 13 kníh.
- V prvej knihe sa zaoberá trojuholníkmi a rovnobežníkmi, končí dôkazom Pytagorovej vety.
- V druhej rozvíja planimetriu.
- V tretej a štvrtej knihe pokračuje v planimetrii, zaoberá sa kruhom a mnohouholníkmi.
- Piata kniha sa týka náuky o pomeroch.
- V šiestej knihe sa venuje otázkam geometrickej podobnosti.
- V ďalších knihách podáva výklad teórie čísel, hovorí o prvočíslach a zložených číslach, dostáva sa až k teórii iracionálnych čísel.
- V jedenástej, dvanástej a trinástej knihe sa zaoberá stereometriou.
Päť Euklidových postulátov
- Každými dvoma bodmi možno preložiť priamku.
- Každú časť priamky možno neobmedzene predĺžiť.
- Z ľubovoľného bodu možno opísať kružnicu s ľubovoľným polomerom.
- Všetky pravé uhly sú zhodné.
- Bodom neležiacim na danej priamke možno viesť práve jednu rovnobežku s danou priamkou.
V Základoch je dôkaz Pytagorovej vety
Euklides poznal konštrukciu zlatého rezu
Rozdeľte úsečku na dve časti tak, aby obdĺžnik, ktorého jedna strana je celá úsečka a druhá jeden z jej dielov, mal rovnaký obsah ako štvorec nad druhým dielom.
alebo
Rozdeľte úsečku na dve časti tak, aby pomer dĺžok malej časti k veľkej časti bol taký istý, ako veľkej časti k celku.
Elektronická verzia Základov
- Existuje aj český preklad Základov, otvor Tu →
- pozri tiež GeoGebra knihu "Eukleidovy Základy ve školské matematice"
Ukážka vety SSS
-
Nech
 a
a
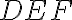 sú dva trojuholníky, ktoré majú dve strany
sú dva trojuholníky, ktoré majú dve strany
 a
a
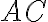 rovné dvom stranám
rovné dvom stranám
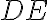 a
a
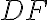 , konkrétne
, konkrétne
 rovnajúce sa
rovnajúce sa
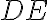 a
a
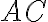 rovná
rovná
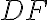 a nech majú základňu
a nech majú základňu
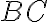 rovnú základni
rovnú základni
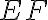 . Hovorím, že uhol
. Hovorím, že uhol
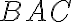 sa rovná aj uhlu
sa rovná aj uhlu
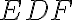 .
.
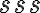 podľa Euklida upravený podľa súčasnej terminológie
podľa Euklida upravený podľa súčasnej terminológie
- Nech trojuholník
 je prenesený na trojuholník
je prenesený na trojuholník
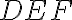 tak, aby bod
tak, aby bod
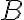 bol umiestnený na bode
bol umiestnený na bode
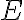 a priamka
a priamka
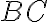 na
na
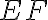 .
.
- Potom bod
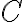 sa prekrýva (zhoduje) s bodom
sa prekrýva (zhoduje) s bodom
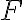 , pretože
, pretože
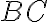 sa rovná
sa rovná
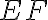 .
. - Ukážeme, že aj úsečka
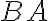 resp.
resp.
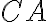 sa prekrýva (zhoduje) s úsečkou
sa prekrýva (zhoduje) s úsečkou
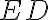 resp.
resp.
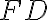 . Budeme dokazovať nepriamo.
. Budeme dokazovať nepriamo. - Nech základňa
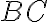 sa prekrýva (zhoduje) so základňou
sa prekrýva (zhoduje) so základňou
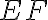 ale strany
ale strany
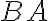 a
a
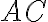 sa neprekrývajú so stranami
sa neprekrývajú so stranami
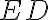 a
a
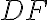 (zobrazia vedľa ako
(zobrazia vedľa ako
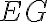 a
a
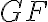 ). Uvažujme prípad, keď bod
). Uvažujme prípad, keď bod
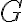 bude v polrovine
bude v polrovine
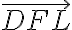 :
:
- →
- Z Euklidovho tvrdenia Proposition 7 (Euclid's Elements, Book I ) vyplýva:
- Keďže trojuholník
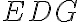 je rovnoramenný, tak uhol
je rovnoramenný, tak uhol
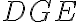 rovná uhlu
rovná uhlu
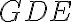 .
. - Z polohy bodu
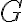 vyplýva, že uhol
vyplýva, že uhol
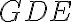 je väčší ako uhol
je väčší ako uhol
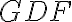 .
. - Tiež trojuholník
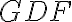 je rovnoramenný, preto aj uhol uhol
je rovnoramenný, preto aj uhol uhol
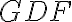 rovná uhlu
rovná uhlu
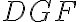 .
. - Z polohy bodu
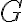 vyplýva, že uhol
vyplýva, že uhol
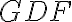 väčší ako uhol
väčší ako uhol
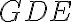 , čo je spor.
, čo je spor. - Preto musí byť bod
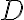 totožný s bodom
totožný s bodom
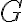 .
. - Podobne postupujeme v prípade, ak bod
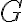 bude v polrovine
bude v polrovine
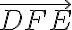 .
.
- Ukázali sme, že strana
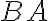 resp.
resp. 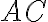 sa prekrýva so stranou
sa prekrýva so stranou 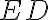 resp.
resp.
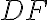 . To znamená, že uhol
. To znamená, že uhol
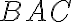 sa rovná uhlu
sa rovná uhlu
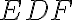 .
. -
Teraz stačí použiť vetu
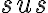 a dostávame tvrdenie: trojuholníky
a dostávame tvrdenie: trojuholníky  a
a
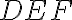 sú zhodné.
sú zhodné.