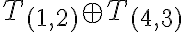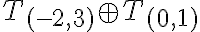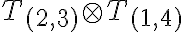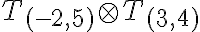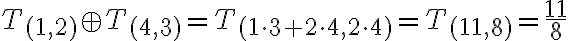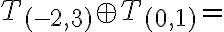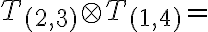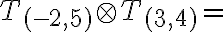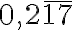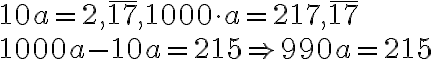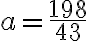Zavedenie číselných oborov N, Z, Q
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Zavedenie číselných oborov N, Z, Q |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | utorok, 7 mája 2024, 07:31 |
Úvodné cvičenie
Riešte.
-
Určte základ
 číselnej sústavy, v ktorej platí:
číselnej sústavy, v ktorej platí: 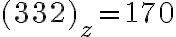 .
. -
Číslo
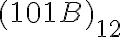 zapíšte v číselnej sústave o základe 5.
zapíšte v číselnej sústave o základe 5. - Doplňte miesto hviezdičiek číslice tak, aby výsledok bol správny: *333 + 2*22 + 66*6 = **9* .
-
Nájdite celé číslo
 a cifru
a cifru
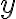 tak, aby
tak, aby
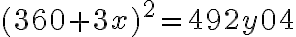 .
. -
Vyriešte rovnicu
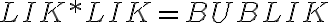 , kde
, kde
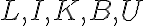 sú cifry v desiatkovej číselnej sústave.
sú cifry v desiatkovej číselnej sústave.
-
Nahraďte písmená číslicami tak, aby platilo
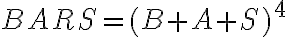 .
.
-
Vyriešte
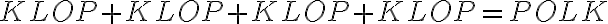 , kde
, kde
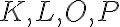 sú cifry v desiatkovej sústave.
sú cifry v desiatkovej sústave.
-
Stanovte číselnú hodnotu výrazu
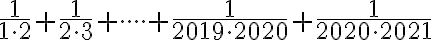 .
. -
Určte posledné dve cifry čísla
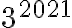 zapísaného v desiatkovej sústave.
zapísaného v desiatkovej sústave.
Riešenie - 1. úloha
Riešenie - 2. úloha
- Číslo
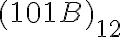 prevedieme najskôr do desiatkovej sústavy:
prevedieme najskôr do desiatkovej sústavy: - Číslo 1751 je zapísané v desiatkovej sústave prevedieme do 5-kovej sústavy:
- použijeme algoritmus postupného delenia číslom 5
Pozri Súbor Excel
- zápis čísla v 5-kovej sústave je
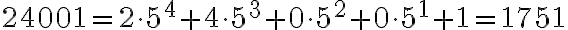 .
.
Riešenie - 3. úloha
Riešenie - 4. úloha
Prirodzené čísla
- Pomocou peanových axióm spočítajte:
- Dokážte, že pre ľubovoľné prirodzené čísla platí: V úlohách 2a a 2b použije matematickú indukciu. V úlohe 2c stačí si uvedomiť, že 1=0'.
- Dokážte, že
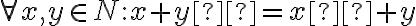 .
. - Trojciferné prirodzené číslo má na mieste jednotiek číslicu 3. Ak túto číslicu premiestnime na začiatok čísla, dostaneme nové číslo, ktoré je rovné trojnásobku pôvodného čísla zväčšeného o 1. Určte takéto trojciferné číslo. [Cirjak, M.: Zbierka divergentných ... úloh. Essox. Prešov 2000.
| 3 + 0 = ... | 3 × 0 = ... |
|---|---|
| 4 + 3 = ... | 4 × 2 = ... |
Riešenia
A. V Peanovej aritmetike budeme dokazovať matematickou indukciou
B. V množinovej aritmetike budeme vychádzať z teórie množín
Budeme vychádzať z platnosti komutatívnosti sčítania pre prirodzené čísla: 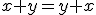 , pričom budeme dokazovať matematickou indukciou.
, pričom budeme dokazovať matematickou indukciou.
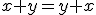 , pričom budeme dokazovať matematickou indukciou.
, pričom budeme dokazovať matematickou indukciou.
Trojciferné prirodzené číslo má na mieste jednotiek číslicu 3. Ak túto číslicu premiestnime na začiatok čísla, dostaneme nové číslo, ktoré je rovné trojnásobku pôvodného čísla zväčšeného o 1. Určte takéto trojciferné číslo.
Matematická indukcia
Dokážte.
Pre 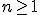 platí:
Pozrite si riešené úlohy na Príklady.eu alebo na Mathematical Induction - Problems With Solutions
platí:
Pozrite si riešené úlohy na Príklady.eu alebo na Mathematical Induction - Problems With Solutions
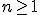 platí:
Pozrite si riešené úlohy na Príklady.eu alebo na Mathematical Induction - Problems With Solutions
platí:
Pozrite si riešené úlohy na Príklady.eu alebo na Mathematical Induction - Problems With Solutions
Riešenia
Riešenie A
Riešenie B
Celé čísla
Riešte.
- Spočítajte a zdôvodnite:
-
Dokážte, že pre ľubovoľné celé čísla
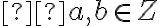 platí:
platí: - Dokážte, že pre dve triedy
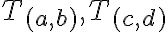 rozkladu
rozkladu
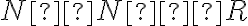 platí :
platí :
![[T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}] [T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/579a44e56178957e0450af29b0cff3be.png)
Ak dve triedy majú spoločný aspoň jeden prvok, tak sa rovnajú! -
Ukážte, že množinu celých čísel možno rozdeliť do troch disjunktných skupín
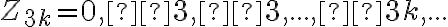 ,
,
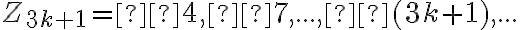
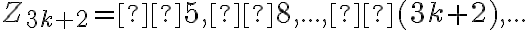 ,
,
kde je prirodzené číslo.
je prirodzené číslo.
-
V množine celých čísel riešte rovnicu
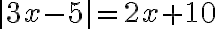 a nerovnicu
a nerovnicu
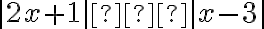 .[B]
.[B]
-
Graficky riešte nerovnicu
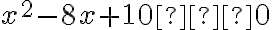 .
. - Dané sú dve celé čísla
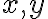 . Súčet súčtu, rozdielu, súčinu a podielu týchto čísel je 150. Určte čísla
. Súčet súčtu, rozdielu, súčinu a podielu týchto čísel je 150. Určte čísla
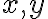 .
. - Čísla
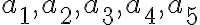 majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
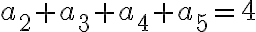 a zároveň
a zároveň
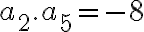 .[B]
.[B]
- Najvýhodnejší počet záclonových úchytiek môžeme vyjadriť postupnosťou: 3, 5, 9, ... Nájdite formulu, ktorá určuje n-tý člen takejto postupnosti.
Riešenie - 1. až 3. úloha
U2: Dokážte, že pre ľubovoľné celé čísla
U3: Dokážte, že pre dve triedy 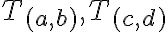 rozkladu
rozkladu
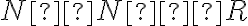 platí:
platí:
![[T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}] [T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/579a44e56178957e0450af29b0cff3be.png)
Ak dve triedy majú spoločný aspoň jeden prvok, tak sa rovnajú!
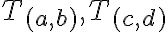 rozkladu
rozkladu
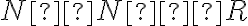 platí:
platí:
![[T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}] [T_{(a,b)} \cap T_{(c,d)} \neq \oslash] \Rightarrow [T_{(a,b)}= T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/579a44e56178957e0450af29b0cff3be.png)
Ak dve triedy majú spoločný aspoň jeden prvok, tak sa rovnajú!
Riešenie - 4. až 9. úloha
Riešenie.
- Pri grafickom riešení nerovnice je potrebné zostrojiť graf kvadratickej funkcie
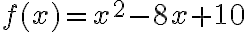 .
. - Najskôr určíme korene rovnice
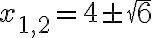 ,
,
pričom s výhodou môžeme pracovať v prostredí GeoGebra. Pozri stránku Kvadratická nerovnica v kurze Did_Mat, zvoľ príklad č.7.
- Potom určíme súradnice vrcholu
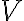 paraboly
paraboly
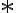 tak, že najskôr určíme hodnotu funkcie
tak, že najskôr určíme hodnotu funkcie
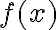 v bode
v bode
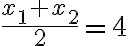
![(f(4)=-6) \Rightarrow (V=[4,-6] ) (f(4)=-6) \Rightarrow (V=[4,-6] )](https://lms.umb.sk/filter/tex/pix.php/d86e333ae6c9d06c9a0dd1d98beb126c.png) .
.
- Riešením nerovnice
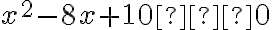 sú čísla
sú čísla
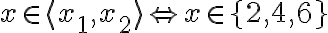
.
Riešenie.
- Hľadáme také dve čísla
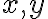 , pre ktoré platí
, pre ktoré platí
(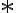 )
)
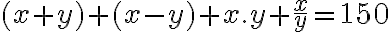 ,
,
pričom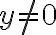 .
. - Prvé tri členy rovnice sú celé čísla, preto musí byť aj podiel
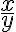
celé číslo , pre ktoré platí
, pre ktoré platí
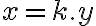 . Po dosadení do rovnice (
. Po dosadení do rovnice (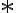 ) dostaneme
) dostaneme
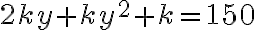 .
.
- Po úprave dostaneme rovnicu
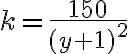 .
.
- Hľadáme druhé mocniny čísel, ktoré sú deliteľmi 150. Zrejme sú to len druhé mocniny čísel 1 a 5.
- Riešením rovnice
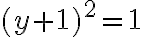 resp.
resp.
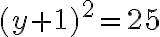
sú čísla
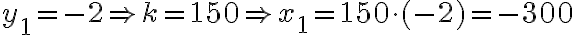
resp.
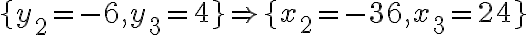 .
. - Hľadané dvojice čísel patria do množiny
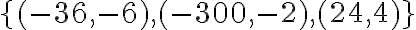
- Urobte skúšku správnosti.
Čísla
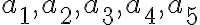 majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
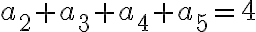 a zároveň
a zároveň
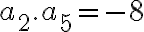 .
.
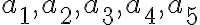 majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
majú vlastnosť, že prvé tri sú po sebe idúce členy geometrickej postupnosti a posledné štyri sú po sebe idúce členy aritmetickej postupnosti. Určte tieto čísla,
ak platí
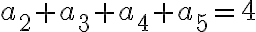 a zároveň
a zároveň
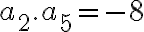 .
.
Riešenie.
-
Nech čísla
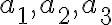 tvoria GeomPost s kvocientom
tvoria GeomPost s kvocientom
 a nech čísla
a nech čísla
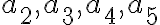 tvoria AritmPost s diferenciou
tvoria AritmPost s diferenciou
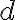 .
.
-
Zo zadania vyplýva, že
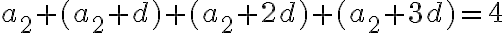 a zároveň
a zároveň
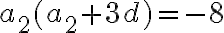 .
.
- To znamená vyriešiť sústavu dvoch rovníc o dvoch nezámych
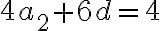
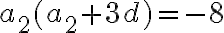 .
.
- Jej riešením sú celé čísla
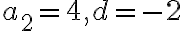 ,
,
odkiaľ dostaneme, že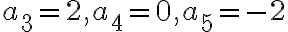 .
.
- Číslo
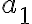 vypočítame tak, že najskôr určíme kvocient
vypočítame tak, že najskôr určíme kvocient
 ako podiel
ako podiel
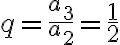
a potom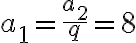 .
.
- Urobte skúšku správnosti.
Počet úchytov na záclone
-
Najjednoduchšie uchytenie záclon je také, pri ktorom máme nepretržite možnosť uchytiť záclonu v strede. Pozri obrázok.
- V prvom kroku použijeme tri úchyty – dva krajné a jeden v strede
- V ďalšom kroku by bolo výhodné, aby sme opäť mohli uchytiť stredy v ľavej aj v pravej časti záclony. To znamená mať dva úchyty pre tieto stredy. Spolu je to 5 úchytov.
- Nasleduje rekurentné vyjadrenie:
- ak máme uchytenú záclonu na
 miestach, tak v ďalšom kroku
miestach, tak v ďalšom kroku
- potrebujeme
 nových úchytov (pre všetky stredy)
nových úchytov (pre všetky stredy)
- spolu je to
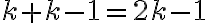 úchytov.
úchytov.
- Dostávame postupnosť, v ktorej
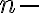 tý člen vyjadríme nasledovne. Začneme experimentovať pre „malé“ hodnoty. Po nie koľkých krokoch môžeme dôjsť k záveru, že pre n-tý člen platí rovnosť:
tý člen vyjadríme nasledovne. Začneme experimentovať pre „malé“ hodnoty. Po nie koľkých krokoch môžeme dôjsť k záveru, že pre n-tý člen platí rovnosť:
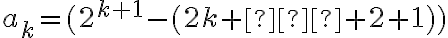 ,
,
ktorá predstavuje súčet dvoch hodnôt. - Prvá je rovná číslu
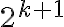 a druhá predstavuje súčet geometrickej postupnosti, kde prvý člen je rovný 1 a koeficient je rovný
a druhá predstavuje súčet geometrickej postupnosti, kde prvý člen je rovný 1 a koeficient je rovný
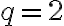 .
.
- Odkiaľ pre súčet dostaneme:
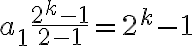 . Po dosadení získame explicitné vyjadrenie pre počet úchytov:
. Po dosadení získame explicitné vyjadrenie pre počet úchytov:

Pri určovaní počtu úchytiek použijeme nasledujúci algoritmus:
Racionálne čísla
Riešte.
- Spočítajte a zdôvodnite v obore racionálnych čísel:
-
Ukážte, že pre ľubovoľné racionálne číslo
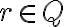 rôzne od nuly existuje racionálne číslo
rôzne od nuly existuje racionálne číslo
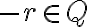 , pre ktoré platí
, pre ktoré platí
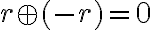 .
. - ukážte, že racionálne číslo
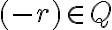 reprezentuje trieda rozkladu
reprezentuje trieda rozkladu
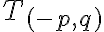 , ak racionálne číslo
, ak racionálne číslo
 reprezentuje trieda
reprezentuje trieda
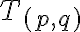 ,
,
- dokážte, že pre ľubovoľné racionálne čísla
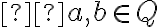 platí:
platí:
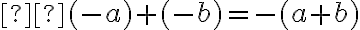 .
.
-
Ukážte, že pre ľubovoľné racionálne číslo
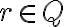 rôzne od nuly existuje racionálne číslo
rôzne od nuly existuje racionálne číslo
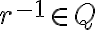 , pre ktoré platí
, pre ktoré platí
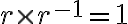 .
. - ukážte, že racionálne číslo
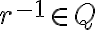 reprezentuje trieda rozkladu
reprezentuje trieda rozkladu
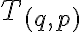 , ak racionálne číslo
, ak racionálne číslo
 reprezentuje trieda
reprezentuje trieda
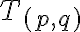 ,
,
- dokážte, že pre ľubovoľné racionálne čísla
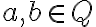 platí:
platí:
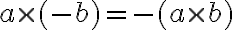 .
.
- Dokážte, že
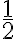 nie je celé číslo.
nie je celé číslo.
-
Pomocou tried rozkladu dokážte, že pre ľubovoľné racionálne čísla
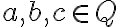 platí komutatívny a asociatívny zákon.
platí komutatívny a asociatívny zákon.
-
V množine racionálnych čísel riešte rovnicu
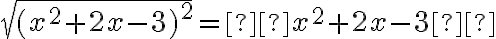 .[B]
.[B]
- Riešte (graficky) nerovnicu
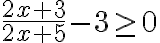 .
. -
Do rovnostranného trojuholníka
 so stranou dĺžky a je vpísaný štvorec
so stranou dĺžky a je vpísaný štvorec
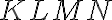 tak, že strana
tak, že strana
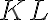 leží na úsečke
leží na úsečke
 . Úsečka
. Úsečka
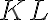 je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov. Str. 496, 49.7[B]
je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov. Str. 496, 49.7[B]
- Nájdite nekonečný desiatkový zápis racionálneho čísla
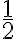 .
. - Vyjadrite číslo
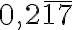 v tvare zlomku.[B]
v tvare zlomku.[B]
Riešenie - úloha 1 až 5
U2 a U3
-
Ukážte, že pre ľubovoľné racionálne číslo
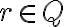 rôzne od nuly existuje racionálne číslo
rôzne od nuly existuje racionálne číslo
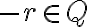 , pre ktoré platí
, pre ktoré platí
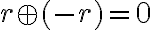 .
. - ukážte, že racionálne číslo
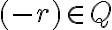 reprezentuje trieda rozkladu
reprezentuje trieda rozkladu
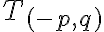 , ak racionálne číslo
, ak racionálne číslo
 reprezentuje trieda
reprezentuje trieda
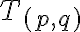 ,
,
- dokážte, že pre ľubovoľné racionálne čísla
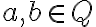 platí:
platí:
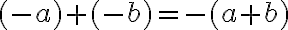 .
.
-
Ukážte, že pre ľubovoľné racionálne číslo
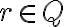 rôzne od nuly existuje racionálne číslo
rôzne od nuly existuje racionálne číslo
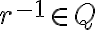 , pre ktoré platí
, pre ktoré platí
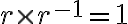 .
.
U2 a U3: Riešenie.
- Pre racionálne číslo
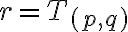 rôzne od nuly
rôzne od nuly
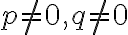 platí
platí 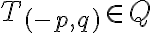 . Označme
. Označme
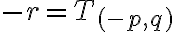 a počítajme
a počítajme
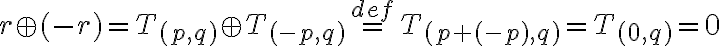
- Nech
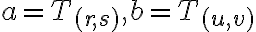 sú racionálne čísla, potom pre súčet racionálnych čísel
sú racionálne čísla, potom pre súčet racionálnych čísel
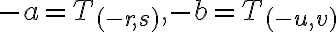 dostaneme
dostaneme
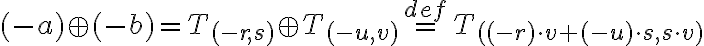
operácie sčítania a násobenia v oboroch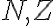 sú komutatívne, asociatívne a disributívne, preto
sú komutatívne, asociatívne a disributívne, preto
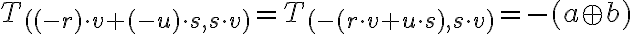
- Zrejme existuje racionálne číslo
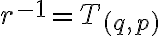 , ktoré spĺňa podmienku
, ktoré spĺňa podmienku
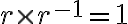 . Počítajme
. Počítajme
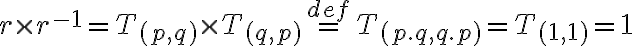 .
Pozrite si model násobenia zlomkov Tu
.
Pozrite si model násobenia zlomkov Tu
Riešenie.
Nech
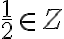 ,
,
potom existujú prirodzené čísla
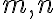 a zároveň platí
a zároveň platí
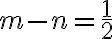 .
.
Po úprave dostaneme
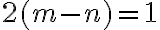 .
.
Na ľavej strane je párne číslo a na pravej nepárne, čo nie je možné. Tým je dôkaz ukončený.
Nech
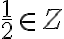 ,
,
potom existujú prirodzené čísla
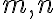 a zároveň platí
a zároveň platí
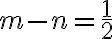 .
.
Po úprave dostaneme
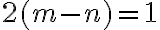 .
.
Na ľavej strane je párne číslo a na pravej nepárne, čo nie je možné. Tým je dôkaz ukončený.
U5: Pomocou tried rozkladu dokážte, že pre ľubovoľné racionálne čísla
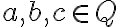 platí komutatívny a asociatívny zákon pre sčítanie.
platí komutatívny a asociatívny zákon pre sčítanie.
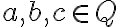 platí komutatívny a asociatívny zákon pre sčítanie.
platí komutatívny a asociatívny zákon pre sčítanie.
Riešenie.
- Dokážeme platnosť komutatívneho zákona. Z definície súčtu dvoch tried
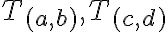 v tomto poradí dostávame
v tomto poradí dostávame
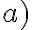
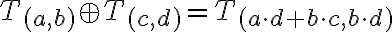
a pre súčet v opačnom poradí dostávame
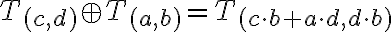
Keďže komutatívny zákon platí pre súčet aj súčin v obore celých čísel, tak zrejme platí aj rovnosť
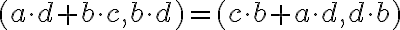 .
.
Odkiaľ vyplýva, že pravá strana vo vzťahu je rovná pravej strane vo vzťahu
je rovná pravej strane vo vzťahu
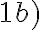 . Preto platí komutatívny zákon pre sčítanie.
. Preto platí komutatívny zákon pre sčítanie. - Dokážeme platnosť asociatívneho zákona. Nech triedy
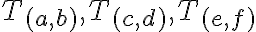 reprezentujú tri racionálne čísla, potom z definície súčtu dostávame
reprezentujú tri racionálne čísla, potom z definície súčtu dostávame
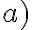
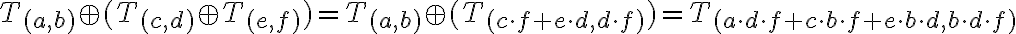
Analogickými úvahami ako v prípade ukážeme, že
ukážeme, že
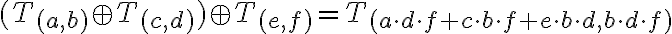
Odkiaľ vyplýva, že pravá strana vo vzťahu je rovná pravej strane vo vzťahu
je rovná pravej strane vo vzťahu
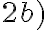 . Preto platí asociatívny zákon.
Tým je dôkaz ukončený.
. Preto platí asociatívny zákon.
Tým je dôkaz ukončený.
- Podobne môžeme postupovať pri dôkaze komutatívnosti a asociatívnosti násobenia racionálnych čísel (DÚ).
Riešenie - úloha 6 až 10
Riešenie.
Zrejme platí
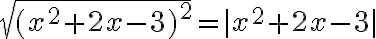
po dosadení dostávame rovnicu
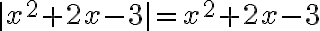 .
.
Kvadratická rovnica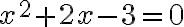 má reálne korene
má reálne korene
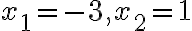 . Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
. Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
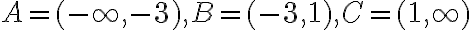 .
.
Zistíme, že riešením danej rovnice v intervaloch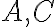 je ľubovoľné racionálne číslo a v intervale
je ľubovoľné racionálne číslo a v intervale
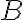 nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
Odpoveď. Riešením sú racionálne čísla množiny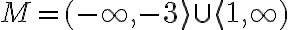 .
.
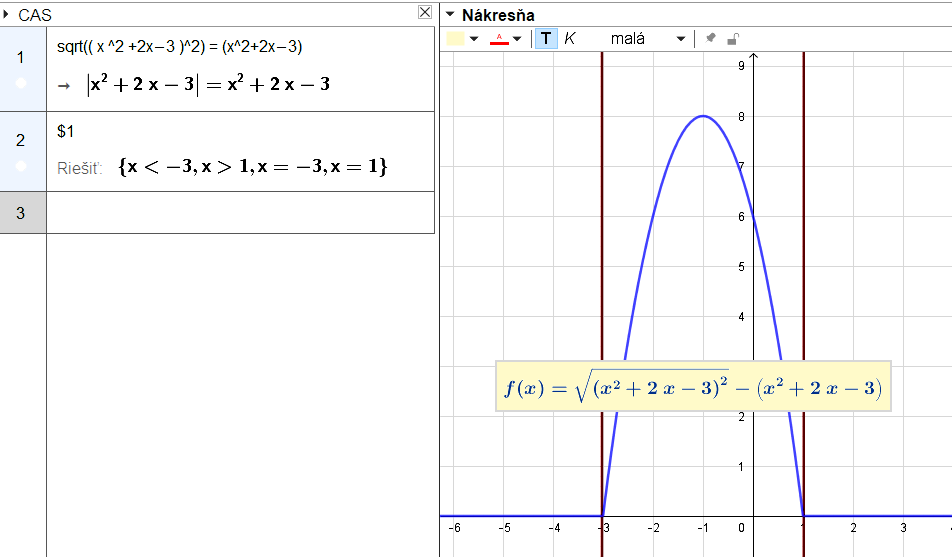
Grafické riešenie - GeoGebra, otvor applet Tu
Zrejme platí
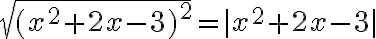
po dosadení dostávame rovnicu
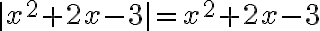 .
.
Kvadratická rovnica
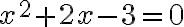 má reálne korene
má reálne korene
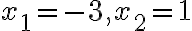 . Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
. Preto budeme riešiť pôvodnú rovnicu samostatne v troch intervaloch
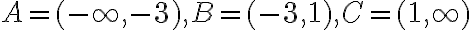 .
.
Zistíme, že riešením danej rovnice v intervaloch
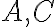 je ľubovoľné racionálne číslo a v intervale
je ľubovoľné racionálne číslo a v intervale
 nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
nemá riešenie. Nakoniec zistíme, že čísla -3 a 1 sú riešením.
Odpoveď. Riešením sú racionálne čísla množiny
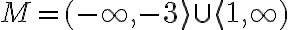 .
.
Grafické riešenie - GeoGebra, otvor applet Tu
U8: Do rovnostranného trojuholníka
 so stranou dĺžky a je vpísaný štvorec
so stranou dĺžky a je vpísaný štvorec
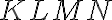 tak, že strana
tak, že strana
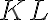 leží na úsečke
leží na úsečke
 . Úsečka
. Úsečka
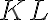 je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
 so stranou dĺžky a je vpísaný štvorec
so stranou dĺžky a je vpísaný štvorec
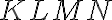 tak, že strana
tak, že strana
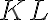 leží na úsečke
leží na úsečke
 . Úsečka
. Úsečka
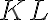 je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
je potom stranou ďalšieho rovnostranného trojuholníka, ktorému je opäť ... Vypočítajte súčet obsahov všetkých takto vzniknutých štvorcov.
Riešenie.
Výška rovnostranného trojuholníka je rovná
je rovná
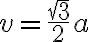
Veľkosť strany štvorca s určíme využitím podobnosti trojuholníkov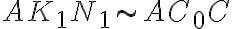 :[1]
:[1]
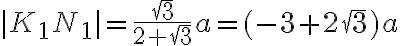 .
.
Pokračujeme určením veľkosti strán ďalších vpísaných štvorcov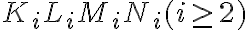 . Potom určíme pomer týchto strán.
. Potom určíme pomer týchto strán.
Dokážte, že v dvoch po sebe idúcich štvorcoch je pomer strán konštatný.
Tento pomer je koeficient geometrického radu, v ktorom pre prvý člen patí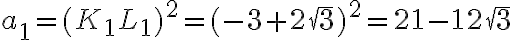 .
.
Výsledok je ...
Výška rovnostranného trojuholníka
 je rovná
je rovná
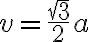
Veľkosť strany štvorca s určíme využitím podobnosti trojuholníkov
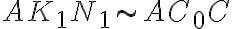 :[1]
:[1]
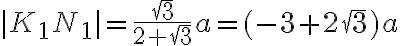 .
.
Pokračujeme určením veľkosti strán ďalších vpísaných štvorcov
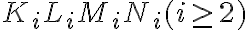 . Potom určíme pomer týchto strán.
. Potom určíme pomer týchto strán.
Dokážte, že v dvoch po sebe idúcich štvorcoch je pomer strán konštatný.
Tento pomer je koeficient geometrického radu, v ktorom pre prvý člen patí
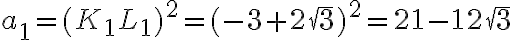 .
.
Výsledok je ...
Pozrite si riešenie od profesora Bukovského[2] Tu.
[1] Bača, M. a kol.: Zbierka riešených a neriešených úloh z matematiky. TU v Košiciach, 2011. Dostupné Tu
[2] Bukovský, L.: Úvod do matematiky. UPJŠ Košice. 2001. Dostupné Tu

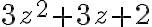
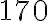
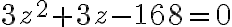
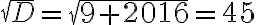
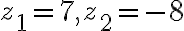
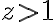
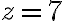
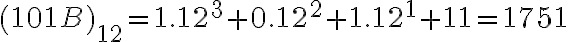
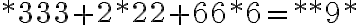
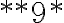
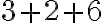
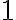
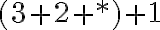
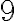
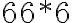
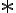
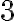
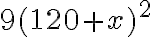
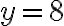
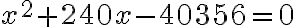
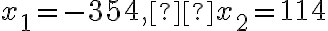
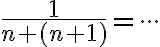
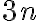
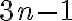
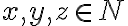
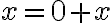
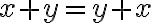
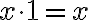
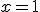
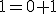
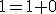
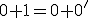
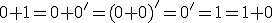
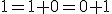
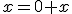
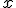
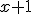
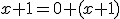
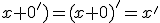
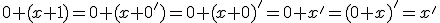
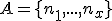
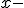
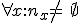
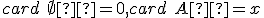
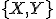
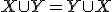
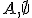
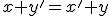
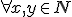
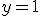
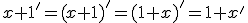
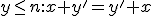
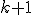
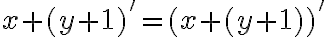
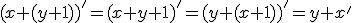
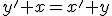
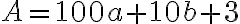
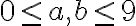
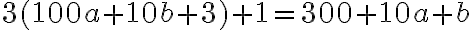
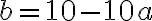
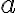
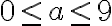
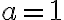
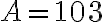
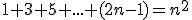
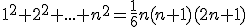
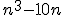
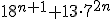
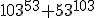
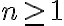
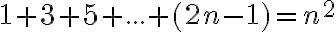
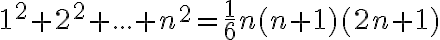
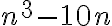
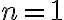
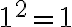
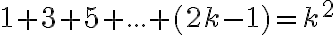
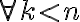
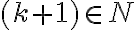
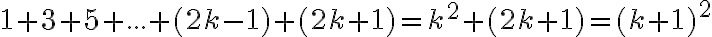
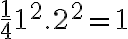
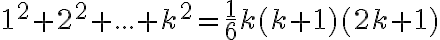
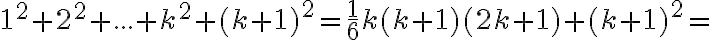
![\frac{1}{6} (k + 1) [ k (2k + 1)+ 6 (k + 1) ] = \frac{1}{6}(k + 1) [ (k + 2) (2k + 3) \frac{1}{6} (k + 1) [ k (2k + 1)+ 6 (k + 1) ] = \frac{1}{6}(k + 1) [ (k + 2) (2k + 3)](https://lms.umb.sk/filter/tex/pix.php/6bb5fdf2c256a11ae7880e9b0a9c2e67.png)

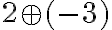
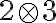
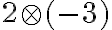
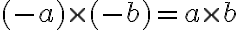
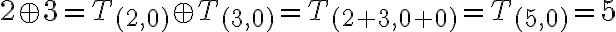
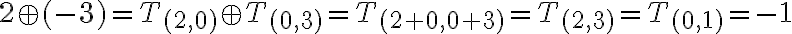
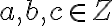
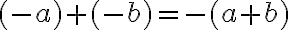
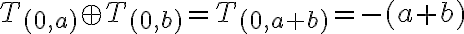
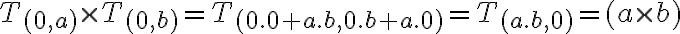
![(m,n) \in T_{(a,b)} \cap T_{(c,d)} \Leftrightarrow [(m,n) \in T_{(a,b)}] \wedge [(m,n) \in T_{(c,d)}] (m,n) \in T_{(a,b)} \cap T_{(c,d)} \Leftrightarrow [(m,n) \in T_{(a,b)}] \wedge [(m,n) \in T_{(c,d)}]](https://lms.umb.sk/filter/tex/pix.php/6b9bb6cec2ff04fcc24551a758137bd7.png)
![[a+m=n+b] \wedge [c+m=n+d] [a+m=n+b] \wedge [c+m=n+d]](https://lms.umb.sk/filter/tex/pix.php/951e9cedff5e1ece6baf75aba0af9439.png)
![[a-c=b-d] [a-c=b-d]](https://lms.umb.sk/filter/tex/pix.php/b4c3d57fae8a94dfc0e6c08d70568562.png)
![[a+d=b+c] [a+d=b+c]](https://lms.umb.sk/filter/tex/pix.php/7e0433909fe3be92805ff6e4f619f58a.png)
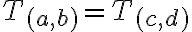
![[(m,n) \in T_{(a,b)}] \Leftrightarrow [T_{(m,n)}= T_{(a,b)}] [(m,n) \in T_{(a,b)}] \Leftrightarrow [T_{(m,n)}= T_{(a,b)}]](https://lms.umb.sk/filter/tex/pix.php/7b0c9bf5006d4d5499b2ae96ffe0e990.png)