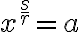Reálne a komplexné čísla
Reálne a komplexné čísla
Mocnina s reálnym exponentom
Záporná pravá strana
Nech reálne číslo  je záporné a nech
je záporné a nech  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 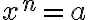
 je záporné a nech
je záporné a nech  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 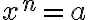
-
V prípade, že
 je párne celé číslo, potom rovnica
je párne celé číslo, potom rovnica 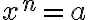
- nemá riešenie v obore reálnych čísel
- v obore komplexných má
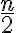 komplexne združených koreňov (Riešte
komplexne združených koreňov (Riešte 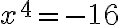 ).
).
-
Ak je
 nepárne, potom rovnica
nepárne, potom rovnica 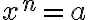 má jeden reálny koreň
má jeden reálny koreň 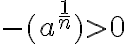 a
a 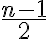 komplexne združených koreňov (Riešte
komplexne združených koreňov (Riešte 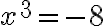 ).
).
Z uvedeného vyplýva, že mocnina s racionálnym exponentom existuje aj pre záporný základ ale v tom prípade musí byť exponent „nepárny“ (prípady 1. a 2.).
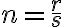
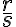

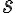
![x^{ \frac{3}{2} }=-27 \Leftrightarrow (-27)^{ \frac{2}{3} }= \sqrt[3]{(-27)^2} = \sqrt[3]{27^2} = \sqrt[3]{9^3} =9>0 x^{ \frac{3}{2} }=-27 \Leftrightarrow (-27)^{ \frac{2}{3} }= \sqrt[3]{(-27)^2} = \sqrt[3]{27^2} = \sqrt[3]{9^3} =9>0](https://lms.umb.sk/filter/tex/pix.php/0930ff8a640ddf217b21ff2adb00634b.png)
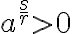
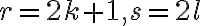
![x^{ \frac{3}{1} }=-27 \Leftrightarrow (-27)^{ \frac{1}{3} }= \sqrt[3]{(-27)^1} = -3 x^{ \frac{3}{1} }=-27 \Leftrightarrow (-27)^{ \frac{1}{3} }= \sqrt[3]{(-27)^1} = -3](https://lms.umb.sk/filter/tex/pix.php/54704b81a2a34b688859939b74705ee2.png)
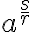
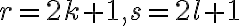
![a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r a^{ \frac {r} {s} }=(a^r )^{ \frac{1}{s} }= \sqrt[s]{a^r} = ( \sqrt[s]{a} )^r=(a^{\frac{1}{s}} )^r](https://lms.umb.sk/filter/tex/pix.php/3e7b97dda331b0af77ba047a99702a02.png)