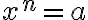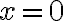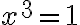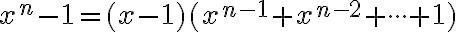Reálne a komplexné čísla
Reálne a komplexné čísla
Mocnina s reálnym exponentom
Nezáporná pravá strana
Ak reálne číslo  je kladné a
je kladné a  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 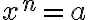 má
má
 je kladné a
je kladné a  je kladné celé číslo, potom rovnica
je kladné celé číslo, potom rovnica 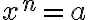 má
má
-
Reálne riešenie
![x= \sqrt[n]{a} x= \sqrt[n]{a}](https://lms.umb.sk/filter/tex/pix.php/7591b7037f09a6a1676ba7bed913935e.png) (zápis aj v tvare
(zápis aj v tvare ![a^{ \frac{1}{n} }: 8^{\frac{1}{3}}= \sqrt[3]{8} =2 a^{ \frac{1}{n} }: 8^{\frac{1}{3}}= \sqrt[3]{8} =2](https://lms.umb.sk/filter/tex/pix.php/18bc46a70060e42cb744e59bf86feb2b.png) ). Skutočnosť, že
). Skutočnosť, že 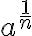 je riešením rovnice vyplýva aj z toho, že po dosadení do ľavej strany rovnice dostaneme
je riešením rovnice vyplýva aj z toho, že po dosadení do ľavej strany rovnice dostaneme - v prípade, že
 je párne, potom riešením rovnice
je párne, potom riešením rovnice 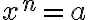 sú aj dva reálne korene, ktoré sú navzájom opačné: t. j.
sú aj dva reálne korene, ktoré sú navzájom opačné: t. j. -
ak je
 nepárne, potom rovnica
nepárne, potom rovnica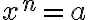 má aj kladný reálny koreň
má aj kladný reálny koreň
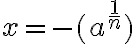 .
.
- Vo všeobecnosti: Ak reálne číslo
 je kladné, tak v obore komplexných čísel má rovnica
je kladné, tak v obore komplexných čísel má rovnica 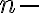 tého stupňa práve
tého stupňa práve  koreňov.
koreňov.
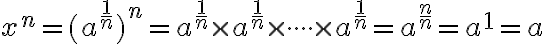
![x_1=a^{ \frac{1}{n} }= \sqrt[n]{a} >0 x_1=a^{ \frac{1}{n} }= \sqrt[n]{a} >0](https://lms.umb.sk/filter/tex/pix.php/513ff965cf0bf4314986fddb07b33cad.png)
![x_2=-(a^{ \frac{1}{n} })= -\sqrt[n]{a} x_2=-(a^{ \frac{1}{n} })= -\sqrt[n]{a}](https://lms.umb.sk/filter/tex/pix.php/9085fe8a62506f64a31b37646e6a6f01.png)