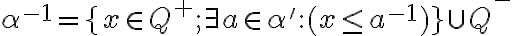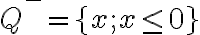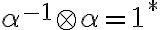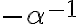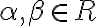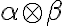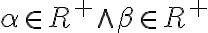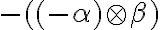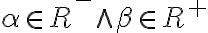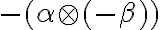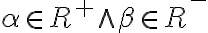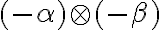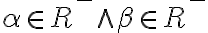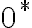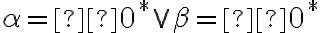Reálne a komplexné čísla
Reálne a komplexné čísla
Dedekindove rezy
Súčin reálnych čísel
Operáciu násobenia dvoch reálnych čísel zavedieme pomocou súčinu kladných Dedekindových rezov.
Definícia
-
Rez
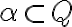 nazveme
kladným Dedekindových rezom, ak dolná časť rezu obsahuje aspoň jedno kladné racionálne číslo:
nazveme
kladným Dedekindových rezom, ak dolná časť rezu obsahuje aspoň jedno kladné racionálne číslo:
 je kladný
je kladný
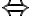
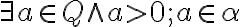 .
. - Množinu všetkých kladných rezov označíme symbolom
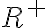 .
.
- ak
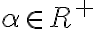 je kladný rez, potom
je kladný rez, potom
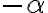 nazývame záporný rez
nazývame záporný rez - rez
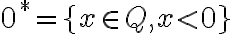 nazývame nulový rez.
nazývame nulový rez.
- množinu všetkých záporných rezov označíme symbolom
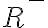 .
.
-
Pre kladné rezy
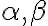 zaveďme súčin kladných rezov:
zaveďme súčin kladných rezov:
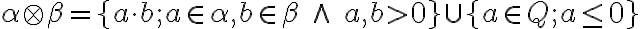 .
.
vytvárame všetky možné súčiny kladných racionálnych čísel z obidvoch rezov, ku ktorým pridáme všetky záporné racionálne čísla vrátane nuly.
K vlastnostiam súčinu viac nájdete v práci: Michal Botur: UVOD DO ARITMETIKY