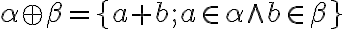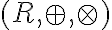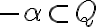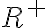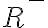Reálne a komplexné čísla
Reálne a komplexné čísla
Dedekindove rezy
Súčet reálnych čísel
Nech
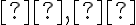 sú dva rezy na množine racionálnych čísel:
sú dva rezy na množine racionálnych čísel:
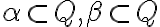 . V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
. V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
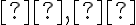 sú dva rezy na množine racionálnych čísel:
sú dva rezy na množine racionálnych čísel:
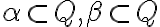 . V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
. V ďalšej časti využijeme fakt, že už vieme sčítať resp. vynásobiť dve racionálne čísla.
Vytvorme množinu
 všetkých možných (racionálnych) súčtov
všetkých možných (racionálnych) súčtov
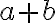 , kde
, kde
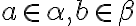 sú racionálne čísla.
sú racionálne čísla.
- Množiny
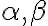 sú neprázdne, preto existujú prvky
sú neprázdne, preto existujú prvky
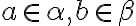 . Množina
. Množina
 je neprázdna, lebo obsahuje racionálne číslo
je neprázdna, lebo obsahuje racionálne číslo
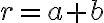 .
. - Ukážeme, že množina
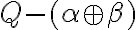 je neprázdna. Množiny
je neprázdna. Množiny
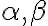 sú rezmi, preto existujú prvky
sú rezmi, preto existujú prvky
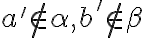 Zrejme pre ľubovoľné prvky
Zrejme pre ľubovoľné prvky
- Nech
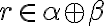 , potom platí
, potom platí
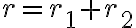 , kde
, kde
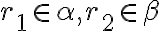 . Nech
. Nech
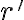 je racionálne číslo, pre ktoré platí
je racionálne číslo, pre ktoré platí
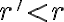 (resp.
(resp.
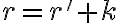 ). Po dosadení dostaneme
). Po dosadení dostaneme
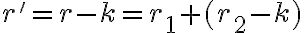 ,
,
čo znamená, že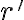 je súčtom dvoch racionálnych čísel.
je súčtom dvoch racionálnych čísel. - Množina
 nemá najväčší prvok. V opačnom prípade, ak by
nemá najväčší prvok. V opačnom prípade, ak by
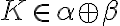 bol najväčší prvok, tak musia existovať dve racionálne čísla
bol najväčší prvok, tak musia existovať dve racionálne čísla
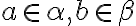 , pričom
, pričom
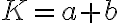 . Bez ujmy na všeobecnosti predpokladajme, že
. Bez ujmy na všeobecnosti predpokladajme, že
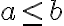 .
.
Keďže je tiež rez, tak nemá najväčší prvok. Musí existovať racionálne číslo
je tiež rez, tak nemá najväčší prvok. Musí existovať racionálne číslo
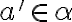 s vlastnosťou
s vlastnosťou
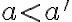 . Relácia
. Relácia
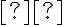 je monotónna, preto
je monotónna, preto
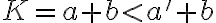 ,
čo je spor s predpokladom, že
,
čo je spor s predpokladom, že
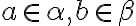 platí
platí
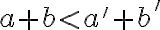 .
.
To znamená, že
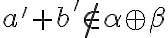 , odkiaľ dostávame, že
, odkiaľ dostávame, že
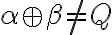 .
.
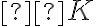 je najväčším prvkom. Tieto tvrdenia nás oprávňujú definovať súčet reálnych ako súčet dedekindových rezov.
je najväčším prvkom. Tieto tvrdenia nás oprávňujú definovať súčet reálnych ako súčet dedekindových rezov.
Definícia
Majme Dedekindove rezy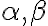 na množine racionálnych čísel. Množinu
na množine racionálnych čísel. Množinu
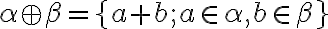 nazveme súčtom reálnych čísel.
nazveme súčtom reálnych čísel.
Majme Dedekindove rezy
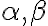 na množine racionálnych čísel. Množinu
na množine racionálnych čísel. Množinu
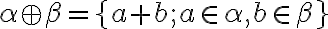 nazveme súčtom reálnych čísel.
nazveme súčtom reálnych čísel.