Reálne a komplexné čísla
Reálne a komplexné čísla
Dedekindove rezy
Reálne čísla zavedieme pomocou Dedekindových rezov na množine racionálnych čísel.
Podmnožinu
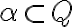 nazývame Dedekindovým rezom množiny
nazývame Dedekindovým rezom množiny
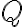 , ak
, ak

Dolná časť nemá najväčší prvok.
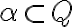 nazývame Dedekindovým rezom množiny
nazývame Dedekindovým rezom množiny
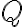 , ak
, ak
- podmnožina
 je neprázdna množina:
je neprázdna množina:
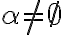
- doplnok
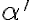 podmnožiny
podmnožiny
 v množine
v množine
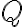 je tiež neprázdny:
je tiež neprázdny:
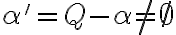 .
. - Nech
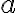 je prvkom rezu
je prvkom rezu
 a nech
a nech
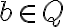 má vlastnosť
má vlastnosť
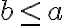 . Potom musí aj racionálne číslo
. Potom musí aj racionálne číslo
 patriť do rezu:
patriť do rezu:
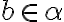 .
. - Rez
 nemá najväčší prvok. Ak
nemá najväčší prvok. Ak
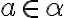 , tak existuje
, tak existuje
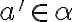 , pre ktoré je
, pre ktoré je
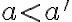 .
.
Dolná časť nemá najväčší prvok.
Definícia.
Množinu všetkých rezov množiny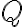 označíme symbolom
označíme symbolom
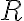 . Prvky patriace do množiny
. Prvky patriace do množiny
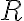 nazývame reálne čísla.
nazývame reálne čísla.
Množinu všetkých rezov množiny
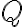 označíme symbolom
označíme symbolom
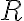 . Prvky patriace do množiny
. Prvky patriace do množiny
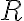 nazývame reálne čísla.
nazývame reálne čísla.
Množinu reálnych čísel sme vytvorili pomocou už známej množiny racionálnych čísel. Proces tvorby sa opiera o podmnožiny
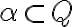 , ktoré majú predpísané štyri vlastnosti.
, ktoré majú predpísané štyri vlastnosti.
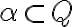 , ktoré majú predpísané štyri vlastnosti.
, ktoré majú predpísané štyri vlastnosti.
-
Prvé dve vlastnosti hovoria, že za podmnožinu
 nemôžeme vziať prázdnu množinu ani množinu všetkých racionálnych čísel.
nemôžeme vziať prázdnu množinu ani množinu všetkých racionálnych čísel. -
Tretia vlastnosť požaduje, aby podmnožina
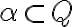 bola „slušne“ usporiadaná:
bola „slušne“ usporiadaná: - ak podmnožina
 obsahuje racionálne číslo
obsahuje racionálne číslo
 , tak táto podmnožina musí obsahovať aj všetky racionálne čísla menšie od čísla
, tak táto podmnožina musí obsahovať aj všetky racionálne čísla menšie od čísla

- ak by sme na číselnej osi zobrazili bod
 reprezentujúci racionálne číslo
reprezentujúci racionálne číslo
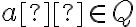 , tak podmnožina
, tak podmnožina
 musí obsahovať polpriamku smerujúcu doľava od bodu
musí obsahovať polpriamku smerujúcu doľava od bodu
 .
.
-
Štvrtú vlastnosť si môžeme interpretovať ako podmnožinu
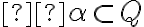 , ktorá zodpovedá sprava otvorenému intervalu
, ktorá zodpovedá sprava otvorenému intervalu 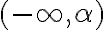 .
. - Reálne čísla, ktoré nie sú racionálne budeme nazývať iracionálne čísla
Vlastnosti rezov.
- Dedekindove rezy, ktorých horná časť má najmenší prvok predstavujú racionálne číslo.
- Nech
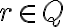 je ľubovoľné ale pevne zvolené racionálne číslo, potom podmnožina
je ľubovoľné ale pevne zvolené racionálne číslo, potom podmnožina
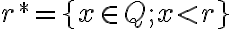 je rezom. Dokážte to.
je rezom. Dokážte to. - Podmnožina
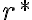 reprezentuje racionálne číslo
reprezentuje racionálne číslo

- množina
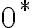 je tiež Dedekindov rez, ktorý (ako neskôr ukážeme) má vlastnosť neutrálneho prvku vzhľadom na sčítanie.
je tiež Dedekindov rez, ktorý (ako neskôr ukážeme) má vlastnosť neutrálneho prvku vzhľadom na sčítanie. - ukážte, že zobrazenie
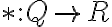 je injektívne.
je injektívne.
- V bode 2. zameňte výrokovú formu
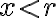 za
za
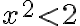 . Dostanete rez
. Dostanete rez
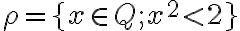 , ktorý reprezentuje iracionálne číslo
, ktorý reprezentuje iracionálne číslo 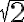 .
.