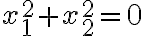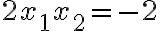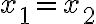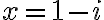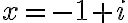Predchádzajúci

Obor komplexných čísel

Príklady

Riešte v obore komplexných čísel rovnicu x^2 = - 2i.
  1. Ak existuje komplexné číslo x , tak ho možno napísať v algebraickom tvare ako x = x_1 + ix_2 .
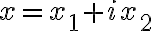  2. Potom naša rovnica bude mať tvar 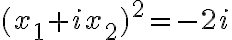( x_1 + ix_2)^2 = - 2i čiže x_1^2 +x_2^2+2ix_1x_2 = - 2i .
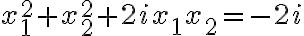  3. Z definície rovnosti komplexných čísel vyplýva, že 
    • reálna časť čísla na ľavej strane tejto rovnice je nula x_1^2 +x_2^2 = 0    - 1. rovnica
    • imaginárna je 2x_1x_2 = - 2                                                                        - 2. rovnica.
  4. Ľavú stranu prvej rovnice rozložíme na súčin podľa vzorca pre rozdiel štvorcov: 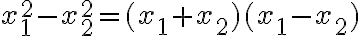x_1^2 - x_2^2 = (x_1 + x_2) (x_1 - x_2) . Tým sa zbavíme druhých mocnín. Vieme, že súčin dvoch čísel sa rovná nule, ak aspoň jeden z činiteľov je rovný nule. Teda buď 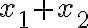x_1 + x_2 , alebo x_1 - x_2  
    • v prvom prípade je x_1=- x_2 v druhom x_1= x_2 . 
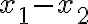
  5.  Ak do druhej rovnice dosadíme 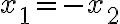x_1=- x_2 dostaneme 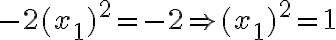-2(x_1)^2 = -2 \Rightarrow (x_1)^2 = 1 . Táto rovnica má dva reálne korene 1, -1 . 
    • pre prvý koreň dostávame x=1-i
    • pre druhý x=-1+i . Ako ľahko overíme, sú obe tieto čísla korene danej rovnice. 
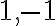  6. Ak predpokladáme, že 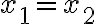x_1=x_2 , tak dosadením do druhej rovnice dostaneme 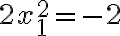2x_1^2=-2 . Táto rovnica však nemá reálne korene!
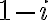Existujú dve komplexné čísla 1 - i a číslo 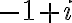-1 + i , ktoré sú koreňmi rovnice x^2 = - 2i.
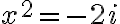Vyriešte tento príklad pomocou goniometrického tvaru komplexného čísla.
Pri riešení rovnice vlastne hľadáme druhú odmocninu komplexného čísla.
Položte si otázku, či vždy existuje druhá odmocnina z komplexného čísla. Pokúste sa dokázať, že áno.
Jarník, Jiří: Komplexní čísla a funkce. Praha: Mladá fronta, 1967. Dostupné na Czech Digital Mathematics Library Tu
\( .\)
Predchádzajúci