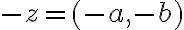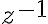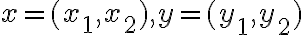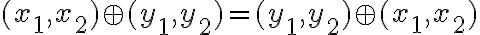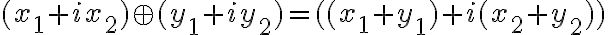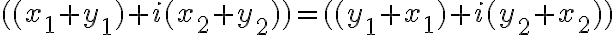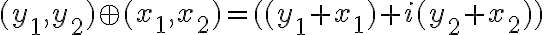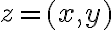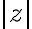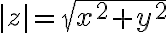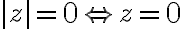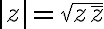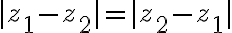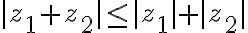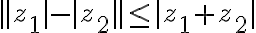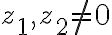Reálne a komplexné čísla
Reálne a komplexné čísla
Obor komplexných čísel
Vlastnosti operácií
Pre súčet a súčin komplexných čísel platí vlastnosť komutatívnosti a asociatívnosti, pričom súčin je distributívny k sčítaniu.
Niektoré algebraické vlastnosti komplexných čísel:
Ukážeme napríklad, že platí komutatívnosť sčítania.
- neutrálny (nulový) prvok pre sčítanie je komplexné číslo
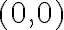
- neutrálny (jednotkový) prvok pre násobenie je komplexné číslo
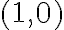
- k ľubovoľnému komplexnému číslu
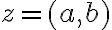 existuje inverzný prvok vzhľadom na sčítanie
existuje inverzný prvok vzhľadom na sčítanie - k ľubovoľnému nenulovému komplexnému číslu
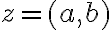 existuje inverzný prvok vzhľadom na súčin
Prvé tri vlastnosti vyplývajú priamo z definície operácií sčítania a násobenia v obore komplexných čísel.
existuje inverzný prvok vzhľadom na súčin
Prvé tri vlastnosti vyplývajú priamo z definície operácií sčítania a násobenia v obore komplexných čísel.
- Dôkaz komutatívnosti:
- Ľavú stranu skúmanej rovnosti upravíme aplikovaním definície súčtu komplexných čísel, ktoré sme vyjadrili v algebrickom tvare
- Pravú stranu rovnosti tiež upravme aplikovaním definície súčtu komplexných čísel.
- V prvom aj v druhom prípade sme dostali rovnaký výsledok. To znamená, že platí komutatívny zákon pre sčítanie komplexných čísel.
- Dokážte štvrtú vlastnosť konštruktívnym spôsobom:
- predpokladajte, že existuje inverzný prvok
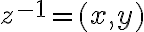 ku komplexnému číslu
ku komplexnému číslu
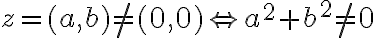
- potom musí platiť rovnosť
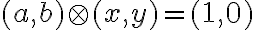 , ale táto rovnosť predstavuje rovnicu o dvoch neznámych
, ale táto rovnosť predstavuje rovnicu o dvoch neznámych
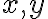
- upravme ju na tvar
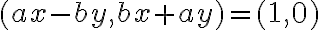 .
. - porovnanie usporiadaných dvojíc vedie na sústavu dvoch rovníc o dvoch neznámych
-
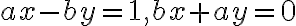 ,
, - ktorej riešením sú reálne čísla
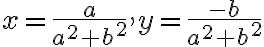 . Pozrite si stránku Matrix calculator.
. Pozrite si stránku Matrix calculator.
Vlastnosti absolútnej hodnoty