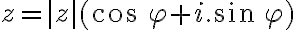Reálne a komplexné čísla
Reálne a komplexné čísla
Obor komplexných čísel
Geometrická interpretácia
Geometrická interpretácia - Gaussova komplexná rovina
Existuje bijektívne zobrazenie
 („prosté“ a „na“) množiny všetkých komplexných čísel
(„prosté“ a „na“) množiny všetkých komplexných čísel
 na euklidovskú rovinu
na euklidovskú rovinu
 :
:
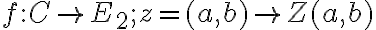 ,
,
kde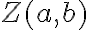 je bod
je bod
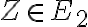 so súradnicami
so súradnicami
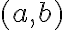 .
.
Ak v rovine zvolíme pravouhlý súradnicový systém, tak obrazom každého komplexného čísla bude práve jeden bod roviny. Obrazom komplexného čísla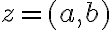 resp.
resp.
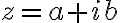 je bod
je bod
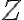 so súradnicami
so súradnicami
 . Pozri obrázok.
. Pozri obrázok.
 („prosté“ a „na“) množiny všetkých komplexných čísel
(„prosté“ a „na“) množiny všetkých komplexných čísel
 na euklidovskú rovinu
na euklidovskú rovinu
 :
:
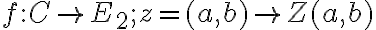 ,
,
kde
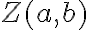 je bod
je bod
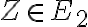 so súradnicami
so súradnicami
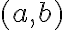 .
.
Ak v rovine zvolíme pravouhlý súradnicový systém, tak obrazom každého komplexného čísla bude práve jeden bod roviny. Obrazom komplexného čísla
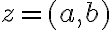 resp.
resp.
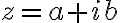 je bod
je bod
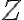 so súradnicami
so súradnicami
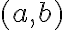 . Pozri obrázok.
. Pozri obrázok.
Zrejme platia rovnosti:
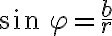 ,
,
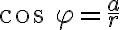 , kde
, kde
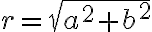 a
a
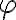 je orientovaný uhol
je orientovaný uhol
 .
.
Číslo predstavuje veľkosť vektora
predstavuje veľkosť vektora
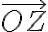 a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
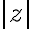 : platí
: platí
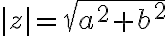 .
.
Z rovností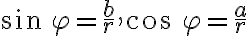 môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
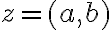 . Dostaneme
. Dostaneme
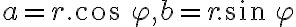 . Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
. Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
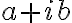 . Dostaneme nový zápis resp. nový tvar komplexného čísla
. Dostaneme nový zápis resp. nový tvar komplexného čísla
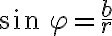 ,
,
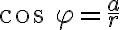 , kde
, kde
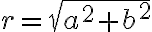 a
a
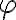 je orientovaný uhol
je orientovaný uhol
 .
.
Číslo
 predstavuje veľkosť vektora
predstavuje veľkosť vektora
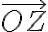 a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
a nazýva sa
absolútna hodnota komplexného čísla a označuje sa symbolom
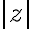 : platí
: platí
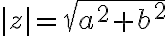 .
.
Z rovností
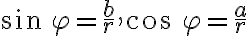 môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
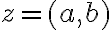 . Dostaneme
. Dostaneme
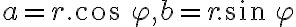 . Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
. Vypočítané hodnoty teraz môžeme dosadiť do algebraického tvaru komplexného čísla
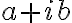 . Dostaneme nový zápis resp. nový tvar komplexného čísla
. Dostaneme nový zápis resp. nový tvar komplexného čísla
Nájdite goniometrický zápis komplexného čísla
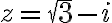 .
.
Riešenie
Najskôr si vypočítame absolútnu hodnotu hľadaného komplexného čísla. Vypočítame, že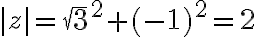 .
.
Potom určíme veľkosť uhla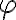 , pre ktorý platí
, pre ktorý platí
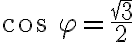 a
a
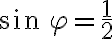 . Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
. Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
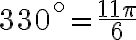 .
.
Goniometrický tvar komplexného čísla je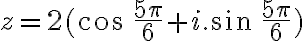 .
.
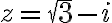 .
.
Riešenie
Najskôr si vypočítame absolútnu hodnotu hľadaného komplexného čísla. Vypočítame, že
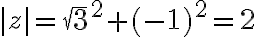 .
.
Potom určíme veľkosť uhla
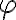 , pre ktorý platí
, pre ktorý platí
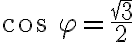 a
a
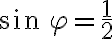 . Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
. Uhol, pre ktorý platia tieto dve rovnosti sa nachádza v IV. kvadrante a jeho veľkosť je
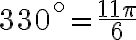 .
.
Goniometrický tvar komplexného čísla je
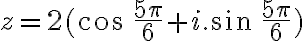 .
.