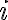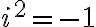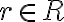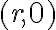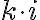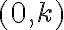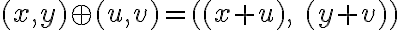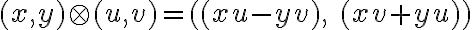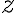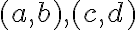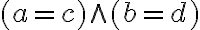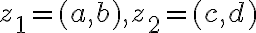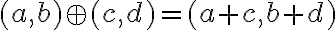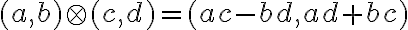Reálne a komplexné čísla
Reálne a komplexné čísla
Obor komplexných čísel
Nech platí
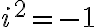 , potom môžeme zaviesť mocninu súčinu
, potom môžeme zaviesť mocninu súčinu 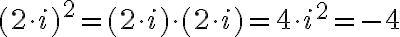 . Vo
všeobecnosti pre ľubovoľné reálne číslo
. Vo
všeobecnosti pre ľubovoľné reálne číslo
 definujeme
definujeme 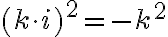 . Čísla
. Čísla
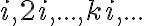 nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
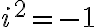 , potom môžeme zaviesť mocninu súčinu
, potom môžeme zaviesť mocninu súčinu 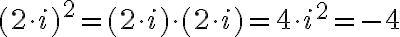 . Vo
všeobecnosti pre ľubovoľné reálne číslo
. Vo
všeobecnosti pre ľubovoľné reálne číslo
 definujeme
definujeme 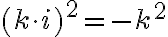 . Čísla
. Čísla
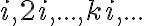 nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
nie sú reálne, sú „imaginárne“. S výhodou môžeme použiť symboliku usporiadaných dvojíc.
Definícia
Nech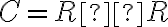 je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
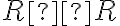 nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
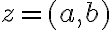 .
.
Nech
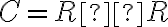 je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
je karteziánsky súčin na množine reálnych čísel, potom prvky karteziánskeho súčinu
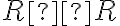 nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
nazveme komplexné čísla. Komplexné čísla sú usporiadané dvojice reálnych čísel
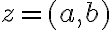 .
.
Poznámky.