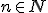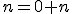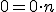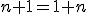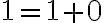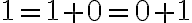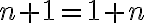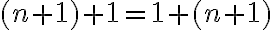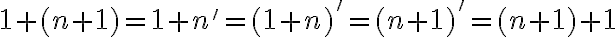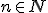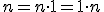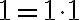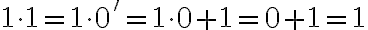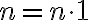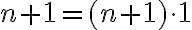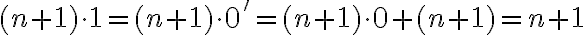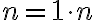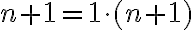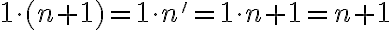Konštrukcia číselných oborov - prirodzené čísla
Vlastnosti operácií
Dôkaz.
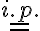 .
.
- Pre
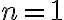 musíme ukázať, že platí rovnosť:
musíme ukázať, že platí rovnosť:
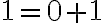 .
.
Upravujme pravú stranu rovnosti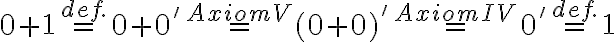 ,
,
čo je ľavá strana rovnosti. -
Predpokladajme (i.p.), že rovnosť
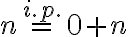 platí pre prirodzené číslo
platí pre prirodzené číslo
 .
.
Musíme ukázať, že platí aj pre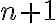 , čo je ekvivalentné s rovnosťou
, čo je ekvivalentné s rovnosťou
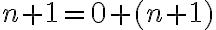 . (1)
Zrejme pre ľavú stranu rovnosti (1) platí
. (1)
Zrejme pre ľavú stranu rovnosti (1) platí
- Zároveň úpravou pravej strany rovnosti (1) dostaneme
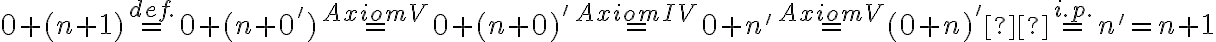 .
.
- Tým je dôkaz ukončený.
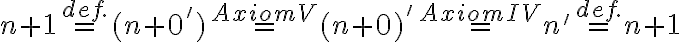 .
.
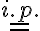 .
.
Dôkaz
- Pre
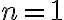 musíme ukázať, že platí rovnosť:
musíme ukázať, že platí rovnosť:
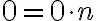 . Z axiómy VI vieme, že platí
. Z axiómy VI vieme, že platí
- Predpokladajme (i.p.), že rovnosť
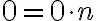 platí pre prirodzené číslo
platí pre prirodzené číslo
 . Musíme ukázať, že platí aj pre
. Musíme ukázať, že platí aj pre
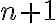 :
:
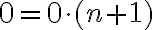 .
.
Upravujme pravú stranu rovnosti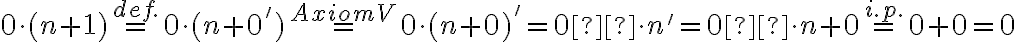 .
.
- Tým je dôkaz ukončený.
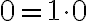 .
.
Jednotka je nasledovník nuly, teda platí
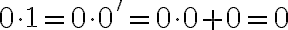 . Teda násobenie nuly a jednotky je komutatívne
. Teda násobenie nuly a jednotky je komutatívne
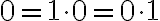 .
.
Dôkaz.