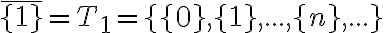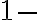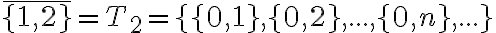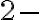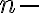Množinová aritmetika
Peano
Množinová aritmetika
Triedy rozkladu
Skúmajme triedy tohto rozkladu
Nech 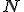 je množina prirodzených čísel a
je množina prirodzených čísel a 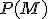 jej potenčná množina. Nech
jej potenčná množina. Nech 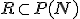 je binárna relácia
je binárna relácia
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) .
.
Potom rozklad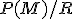 bude obsahovať napríklad triedu:
bude obsahovať napríklad triedu:
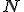 je množina prirodzených čísel a
je množina prirodzených čísel a 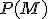 jej potenčná množina. Nech
jej potenčná množina. Nech 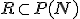 je binárna relácia
je binárna relácia
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) .
.
Potom rozklad
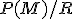 bude obsahovať napríklad triedu:
bude obsahovať napríklad triedu:
Označenie pre triedy rozkladov
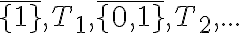 môžeme nahradiť jednoducho symbolmi
môžeme nahradiť jednoducho symbolmi
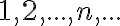 , čo sú vlastne arabské číslice pre označenie prirodzených čísel.
, čo sú vlastne arabské číslice pre označenie prirodzených čísel.
-
Triedu rozkladu, ktorá prináleží prázdnej množine
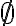 môžeme zapísať v tvare:
môžeme zapísať v tvare:
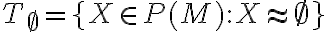 . Zrejme obsahuje len jednu množinu a to je práve prázdna množina. Teda
. Zrejme obsahuje len jednu množinu a to je práve prázdna množina. Teda
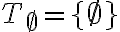 obsahuje jednu množinu, ktorá má nula prvkov.
obsahuje jednu množinu, ktorá má nula prvkov. - Triedu rozkladu, ktorá prináleží množine
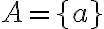 môžeme zapísať v tvare:
môžeme zapísať v tvare:
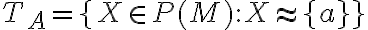 . Prvkami tejto triedy sú všetky množiny, ktoré
majú práve jeden prvok
. Prvkami tejto triedy sú všetky množiny, ktoré
majú práve jeden prvok
- Ak zvolíme konečnú množinu
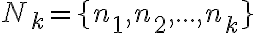 , tak trieda rozkladu prislúchajúca množine
, tak trieda rozkladu prislúchajúca množine
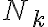 bude obsahovať všetky množiny, ktoré obsahujú práve
bude obsahovať všetky množiny, ktoré obsahujú práve
 prvkov.
prvkov.