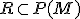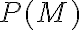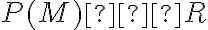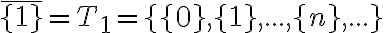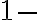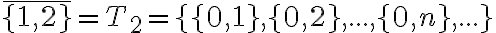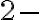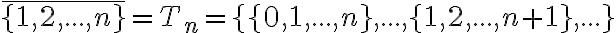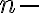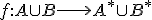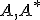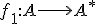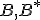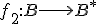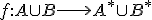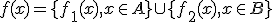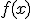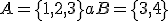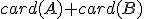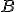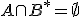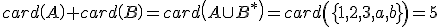Množinová aritmetika
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Vybrané kapitoly z aritmetiky a analytickej geometrie |
| Kniha: | Množinová aritmetika |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 13:30 |
Opis
Peano
Množinová aritmetika
Ústredným pojmom pri množinovom prístupe v aritmetike prirodzených čísel je pojem ekvivalentnosti dvoch množín.
Pri jeho zavedení sa budeme opierať o bijektívne zobrazenie medzi dvoma množinami. Pri konečných množinách si takéto zobrazenie môžeme predstaviť tak, že prvky dvoch množín navzájom pospájame podľa pravidla „jeden len s jedným“. Takéto pravidlo používajú
aj deti na prvom stupni ZŠ.
Definícia.
Hovoríme, že množina je ekvivalentná s množinou
je ekvivalentná s množinou  , ak existuje prosté zobrazenie
, ak existuje prosté zobrazenie 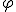 množiny
množiny  na množinu
na množinu  .
.
Skutočnosť, že množina je ekvivalentná s množinou
je ekvivalentná s množinou  budeme zapisovať symbolom
budeme zapisovať symbolom 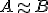 . Zobrazenie
. Zobrazenie 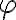 je zrejme bijekcia.
je zrejme bijekcia.
Hovoríme, že množina
 je ekvivalentná s množinou
je ekvivalentná s množinou  , ak existuje prosté zobrazenie
, ak existuje prosté zobrazenie 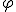 množiny
množiny  na množinu
na množinu  .
.
Skutočnosť, že množina
 je ekvivalentná s množinou
je ekvivalentná s množinou  budeme zapisovať symbolom
budeme zapisovať symbolom 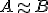 . Zobrazenie
. Zobrazenie 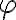 je zrejme bijekcia.
je zrejme bijekcia.
Príklad.
Nech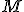 je nekonečná množina a
je nekonečná množina a 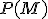 jej potenčná množina. Definujme binárnu reláciu
jej potenčná množina. Definujme binárnu reláciu 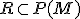 tak, aby
tak, aby
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/782f09dd57dd917afb64567badbf371d.png) .
.
Nech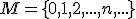 je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
Nech
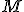 je nekonečná množina a
je nekonečná množina a 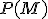 jej potenčná množina. Definujme binárnu reláciu
jej potenčná množina. Definujme binárnu reláciu 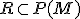 tak, aby
tak, aby
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/782f09dd57dd917afb64567badbf371d.png) .
.
Nech
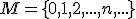 je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
je množina prirodzených čísel. Zistite, či táto relácia je symetrická. Vypíšte jej niektoré prvky - dvojice podmnožín.
Ekvivalentné množiny
Nasledujúca veta hovorí, že relácia
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) je reláciou ekvivalencie na množine
je reláciou ekvivalencie na množine
 . Preto existuje rozklad tejto množiny na disjunktné triedy.
. Preto existuje rozklad tejto množiny na disjunktné triedy.
Toto je východiskom pre zavedenie prirodzených čísel ako kardinálnych čísel, ak za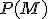 zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) je reláciou ekvivalencie na množine
je reláciou ekvivalencie na množine
 . Preto existuje rozklad tejto množiny na disjunktné triedy.
. Preto existuje rozklad tejto množiny na disjunktné triedy.
Toto je východiskom pre zavedenie prirodzených čísel ako kardinálnych čísel, ak za
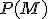 zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
Dôkaz.
- Binárna relácia
![R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/dabe6bc68c09e7e69633233768f9a779.png) je zrejme reflexívna. Stačí uvažovať o identickom zobrazení na množine
je zrejme reflexívna. Stačí uvažovať o identickom zobrazení na množine
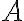 , ktoré je zrejme bijektívne. V takom prípade dostaneme
, ktoré je zrejme bijektívne. V takom prípade dostaneme
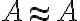 , z čoho vyplýva
, z čoho vyplýva
![[A,A] \in R [A,A] \in R](https://lms.umb.sk/filter/tex/pix.php/08e96854159213bbdf3ddd36689f71c1.png) .
. - Pre ľubovoľnú usporiadanú dvojicu
![[A,B] \in R [A,B] \in R](https://lms.umb.sk/filter/tex/pix.php/55203b628fe423a1f76ad4576efd3c28.png) musí v zmysle definície relácie
musí v zmysle definície relácie
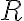 existovať bijekcia
existovať bijekcia
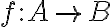 . Uvažujme o inverznom zobrazení
. Uvažujme o inverznom zobrazení
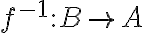 . Také zobrazenie existuje a zrejme je aj bijektívne. To znamená, že platí
. Také zobrazenie existuje a zrejme je aj bijektívne. To znamená, že platí
![[B,A] \in R [B,A] \in R](https://lms.umb.sk/filter/tex/pix.php/acad670a102ae38b5b3b5da3b5d83c5c.png) . Tým sme dokázali, že
. Tým sme dokázali, že
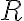 je symetrická.
je symetrická. - Tranzitívnosť relácie vyplýva z toho, že zloženie dvoch bijektívnych zobrazení je bijekcia.
Triedy rozkladu
Skúmajme triedy tohto rozkladu
Nech 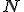 je množina prirodzených čísel a
je množina prirodzených čísel a 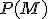 jej potenčná množina. Nech
jej potenčná množina. Nech 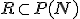 je binárna relácia
je binárna relácia
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) .
.
Potom rozklad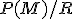 bude obsahovať napríklad triedu:
bude obsahovať napríklad triedu:
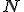 je množina prirodzených čísel a
je množina prirodzených čísel a 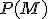 jej potenčná množina. Nech
jej potenčná množina. Nech 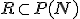 je binárna relácia
je binárna relácia
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) .
.
Potom rozklad
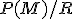 bude obsahovať napríklad triedu:
bude obsahovať napríklad triedu:
Označenie pre triedy rozkladov
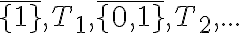 môžeme nahradiť jednoducho symbolmi
môžeme nahradiť jednoducho symbolmi
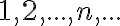 , čo sú vlastne arabské číslice pre označenie prirodzených čísel.
, čo sú vlastne arabské číslice pre označenie prirodzených čísel.
-
Triedu rozkladu, ktorá prináleží prázdnej množine
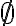 môžeme zapísať v tvare:
môžeme zapísať v tvare:
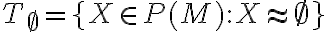 . Zrejme obsahuje len jednu množinu a to je práve prázdna množina. Teda
. Zrejme obsahuje len jednu množinu a to je práve prázdna množina. Teda
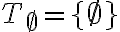 obsahuje jednu množinu, ktorá má nula prvkov.
obsahuje jednu množinu, ktorá má nula prvkov. - Triedu rozkladu, ktorá prináleží množine
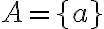 môžeme zapísať v tvare:
môžeme zapísať v tvare:
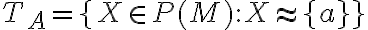 . Prvkami tejto triedy sú všetky množiny, ktoré
majú práve jeden prvok
. Prvkami tejto triedy sú všetky množiny, ktoré
majú práve jeden prvok
- Ak zvolíme konečnú množinu
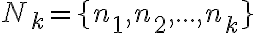 , tak trieda rozkladu prislúchajúca množine
, tak trieda rozkladu prislúchajúca množine
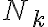 bude obsahovať všetky množiny, ktoré obsahujú práve
bude obsahovať všetky množiny, ktoré obsahujú práve
 prvkov.
prvkov.
Kardinálne číslo množiny
Definícia.
Každej triede rozkladu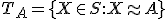 na systéme
na systéme  všetkých množín priradíme symbol, ktorý nazveme
všetkých množín priradíme symbol, ktorý nazveme
kardinálne číslo množiny .
.
Symboly používané pre kardinálne číslo množiny sú:
sú: 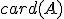 alebo
alebo 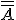 , prípadne
, prípadne  .
.
Každej triede rozkladu
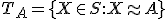 na systéme
na systéme  všetkých množín priradíme symbol, ktorý nazveme
všetkých množín priradíme symbol, ktorý nazveme
kardinálne číslo množiny
 .
.
Symboly používané pre kardinálne číslo množiny
 sú:
sú: 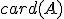 alebo
alebo 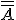 , prípadne
, prípadne  .
.
S kardinálnymi číslami sa stretávajú už žiaci na ZŠ. Napríklad pomocou nasledujúceho diagramu ukážu žiaci na prvom stupni ZŠ, že počet „krúžkov“ v prvej skupinke je rovný počtu „štvorčekov“ v druhej skupinke.
Spoločnú vlastnosť týchto dvoch skupín neskôr pomenujú slovom tri a na označenie použijú arabskú číslicu 3.
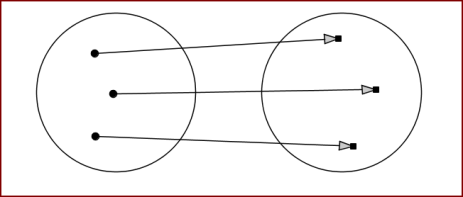
Terminológiu teórie množín v zásade nepoužívajú, ale používajú termíny ako skupina, hromada, a pod. Uvedomte si, že grafické spájanie predstavuje prosté zobrazenie z jednej do druhej množiny.
Spoločnú vlastnosť týchto dvoch skupín neskôr pomenujú slovom tri a na označenie použijú arabskú číslicu 3.

Terminológiu teórie množín v zásade nepoužívajú, ale používajú termíny ako skupina, hromada, a pod. Uvedomte si, že grafické spájanie predstavuje prosté zobrazenie z jednej do druhej množiny.
Prirodzené čísla ako kardinálne čísla.
Nech je nekonečná množina a nech
je nekonečná množina a nech 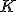 je ľubovoľná konečná podmnožina
množiny
je ľubovoľná konečná podmnožina
množiny  . Potom množina
. Potom množina
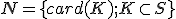
je množina prirodzených čísel.
Nech
 je nekonečná množina a nech
je nekonečná množina a nech 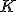 je ľubovoľná konečná podmnožina
množiny
je ľubovoľná konečná podmnožina
množiny  . Potom množina
. Potom množina
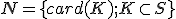
je množina prirodzených čísel.
Nasledujúci príklad je z pracovného listu prvý ročník základnej školy hovorí o kardinálnom čísle množiny, ktorá má práve štyri prvky. Žiaci sú nútení abstrahovať od farby a veľkosti jabĺk v skupine. Príklad môže byť modifikovaný rôznymi typmi otázok.
Napríklad môžeme sa pýtať, koľko je červených jabĺk a pod.
Príklad.
Na obrázku sú jablká rôznej farby a veľkosti. Pýtame sa: Koľko jabĺk vidíme na obrázku?

Odpovedáme: Na obrázku vidíme 4 jablká.
Na obrázku sú jablká rôznej farby a veľkosti. Pýtame sa: Koľko jabĺk vidíme na obrázku?
Odpovedáme: Na obrázku vidíme 4 jablká.
Súčet
Definícia - sčítanie kardinálnych čísel.
Nech sú dve konečné a zároveň disjunktné množiny, ktorých kardinálne čísla sú
sú dve konečné a zároveň disjunktné množiny, ktorých kardinálne čísla sú 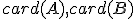 .
Pod súčtom týchto kardinálnych čísel budeme rozumieť kardinálne číslo zjednotenia
.
Pod súčtom týchto kardinálnych čísel budeme rozumieť kardinálne číslo zjednotenia 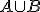
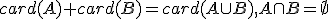
V definícii predpokladáme, že množiny sú disjunktné.
sú disjunktné.
Nech
 sú dve konečné a zároveň disjunktné množiny, ktorých kardinálne čísla sú
sú dve konečné a zároveň disjunktné množiny, ktorých kardinálne čísla sú 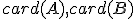 .
Pod súčtom týchto kardinálnych čísel budeme rozumieť kardinálne číslo zjednotenia
.
Pod súčtom týchto kardinálnych čísel budeme rozumieť kardinálne číslo zjednotenia 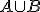
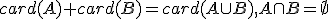
V definícii predpokladáme, že množiny
 sú disjunktné.
sú disjunktné.
Ak množiny  nie sú disjunktné, tak vieme nájsť množiny
nie sú disjunktné, tak vieme nájsť množiny  , ktoré budú disjunktné a zároveň bude platiť
, ktoré budú disjunktné a zároveň bude platiť
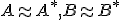 .
.
Potom pod súčtom kardinálnych čísel množín budeme rozumieť súčet kardinálnych čísel množín
budeme rozumieť súčet kardinálnych čísel množín 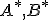
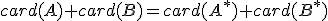 .
.
Ak má byť definícia súčtu dvoch kardinálnych čísel korektná, tak nemôže závisieť od výberu množín .
.
 nie sú disjunktné, tak vieme nájsť množiny
nie sú disjunktné, tak vieme nájsť množiny  , ktoré budú disjunktné a zároveň bude platiť
, ktoré budú disjunktné a zároveň bude platiť
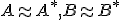 .
.
Potom pod súčtom kardinálnych čísel množín
 budeme rozumieť súčet kardinálnych čísel množín
budeme rozumieť súčet kardinálnych čísel množín 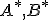
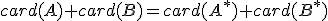 .
.
Ak má byť definícia súčtu dvoch kardinálnych čísel korektná, tak nemôže závisieť od výberu množín
 .
.
Veta - o súčte kardinálnych čísel.
Nech sú množiny, pre ktoré platí
sú množiny, pre ktoré platí 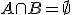 a nech
a nech 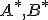 sú ľubovoľné disjunktné množiny,
pre ktoré platí
sú ľubovoľné disjunktné množiny,
pre ktoré platí 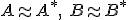 . Potom platí:
. Potom platí:
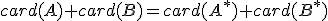
Nech
 sú množiny, pre ktoré platí
sú množiny, pre ktoré platí 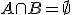 a nech
a nech 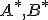 sú ľubovoľné disjunktné množiny,
pre ktoré platí
sú ľubovoľné disjunktné množiny,
pre ktoré platí 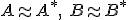 . Potom platí:
. Potom platí:
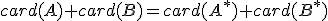
Násobenie
Definícia - súčin kardinálnych čísel.
Nech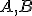 sú dve konečné, ktorých kardinálne čísla sú
sú dve konečné, ktorých kardinálne čísla sú 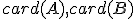 .
Pod súčinom týchto kardinálnych čísel budeme rozumieť kardinálne číslo karteziánskeho súčinu
.
Pod súčinom týchto kardinálnych čísel budeme rozumieť kardinálne číslo karteziánskeho súčinu 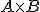
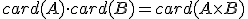 .
.
Nech
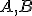 sú dve konečné, ktorých kardinálne čísla sú
sú dve konečné, ktorých kardinálne čísla sú 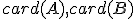 .
Pod súčinom týchto kardinálnych čísel budeme rozumieť kardinálne číslo karteziánskeho súčinu
.
Pod súčinom týchto kardinálnych čísel budeme rozumieť kardinálne číslo karteziánskeho súčinu 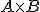
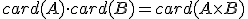 .
.
Veta.
Pre karteziánsky súčin dvoch množín platí komutatívny a asociatívny zákon. To znamená, že násobenie kardinálnych čísel je
komutatívne aj asociatívne
distributívne voči sčítaniu.
Pre karteziánsky súčin dvoch množín platí komutatívny a asociatívny zákon. To znamená, že násobenie kardinálnych čísel je
komutatívne aj asociatívne
distributívne voči sčítaniu.
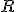
![\small [ \lbrace{0}\rbrace, \lbrace{0}\rbrace], [ \lbrace{0}\rbrace, \lbrace{1}\rbrace], ...,[ \lbrace{0}\rbrace, \lbrace{n}\rbrace], ... \small [ \lbrace{0}\rbrace, \lbrace{0}\rbrace], [ \lbrace{0}\rbrace, \lbrace{1}\rbrace], ...,[ \lbrace{0}\rbrace, \lbrace{n}\rbrace], ...](https://lms.umb.sk/filter/tex/pix.php/22286cf5621be8d62cbd77f375365f45.png)
![\small [ \lbrace{0,1}\rbrace, \lbrace{0,2}\rbrace], ...,[\lbrace{0,1}\rbrace,\lbrace{0,n}\rbrace], ...,[ \lbrace{1,2}\rbrace,,\lbrace{1,n}\rbrace], ... \small [ \lbrace{0,1}\rbrace, \lbrace{0,2}\rbrace], ...,[\lbrace{0,1}\rbrace,\lbrace{0,n}\rbrace], ...,[ \lbrace{1,2}\rbrace,,\lbrace{1,n}\rbrace], ...](https://lms.umb.sk/filter/tex/pix.php/b7976e0c2c7122ebcaf715e584400a50.png)
![\small [ \lbrace{0,1,2}\rbrace, \lbrace{0,1,3}\rbrace], ..., [ \lbrace{1,2,3}\rbrace,\lbrace{1,2,,n}\rbrace], ... \small [ \lbrace{0,1,2}\rbrace, \lbrace{0,1,3}\rbrace], ..., [ \lbrace{1,2,3}\rbrace,\lbrace{1,2,,n}\rbrace], ...](https://lms.umb.sk/filter/tex/pix.php/44c53c81d9e2ebbf1dcf847abc5fe996.png)