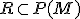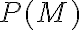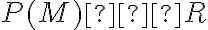Množinová aritmetika
Peano
Množinová aritmetika
Ekvivalentné množiny
Nasledujúca veta hovorí, že relácia
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) je reláciou ekvivalencie na množine
je reláciou ekvivalencie na množine
 . Preto existuje rozklad tejto množiny na disjunktné triedy.
. Preto existuje rozklad tejto množiny na disjunktné triedy.
Toto je východiskom pre zavedenie prirodzených čísel ako kardinálnych čísel, ak za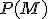 zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
![\small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace \small R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/957577dc49b442d82d1ff43066747a64.png) je reláciou ekvivalencie na množine
je reláciou ekvivalencie na množine
 . Preto existuje rozklad tejto množiny na disjunktné triedy.
. Preto existuje rozklad tejto množiny na disjunktné triedy.
Toto je východiskom pre zavedenie prirodzených čísel ako kardinálnych čísel, ak za
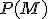 zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
zvolíme množinu všetkých
konečných podmnožín nejakej nekonečnej množiny. Existenciu nekonečnej množiny zabezpečuje axióma z teórie množín.
Dôkaz.
- Binárna relácia
![R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace R= \lbrace{ [A,B] \in P(M) \times P(M): A \approx B}\rbrace](https://lms.umb.sk/filter/tex/pix.php/dabe6bc68c09e7e69633233768f9a779.png) je zrejme reflexívna. Stačí uvažovať o identickom zobrazení na množine
je zrejme reflexívna. Stačí uvažovať o identickom zobrazení na množine
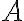 , ktoré je zrejme bijektívne. V takom prípade dostaneme
, ktoré je zrejme bijektívne. V takom prípade dostaneme
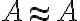 , z čoho vyplýva
, z čoho vyplýva
![[A,A] \in R [A,A] \in R](https://lms.umb.sk/filter/tex/pix.php/08e96854159213bbdf3ddd36689f71c1.png) .
. - Pre ľubovoľnú usporiadanú dvojicu
![[A,B] \in R [A,B] \in R](https://lms.umb.sk/filter/tex/pix.php/55203b628fe423a1f76ad4576efd3c28.png) musí v zmysle definície relácie
musí v zmysle definície relácie
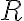 existovať bijekcia
existovať bijekcia
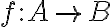 . Uvažujme o inverznom zobrazení
. Uvažujme o inverznom zobrazení
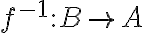 . Také zobrazenie existuje a zrejme je aj bijektívne. To znamená, že platí
. Také zobrazenie existuje a zrejme je aj bijektívne. To znamená, že platí
![[B,A] \in R [B,A] \in R](https://lms.umb.sk/filter/tex/pix.php/acad670a102ae38b5b3b5da3b5d83c5c.png) . Tým sme dokázali, že
. Tým sme dokázali, že
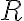 je symetrická.
je symetrická. - Tranzitívnosť relácie vyplýva z toho, že zloženie dvoch bijektívnych zobrazení je bijekcia.