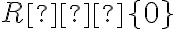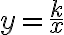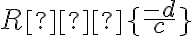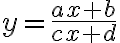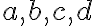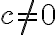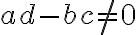Funkcie: Lineárna lomená funkcia

Elementárne funkcie

Lineárna lomená funkcia

Žiaci by už mali byť oboznámení s funkciou nepriama úmernosť, preto je vhodné použiť nejaký motivačný príklad tohto špecifického prípadu lomenej funkcie

Nepriama úmernosť je každá funkcia na množine

$R∖\lbrace{0}\rbrace$ daná v tvare

$y= \frac{k}{x}$ ,
kde

$k$ je reálne číslo rôzne od nuly

Vyhľadajte aktivity v GeoGebre, napríklad Lineárna lomená funkcia (František Legát)

Grafom nepriamej úmernosti je krivka, ktorá sa nazýva rovnoosá hyperbola.

Najskôr zostrojíme graf funkcie 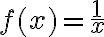$f(x)= \frac{1}{x}$ , ktorý možno zostrojiť na základe tabuľky s dostatočným počtom rôznych hodnôt pre $x$ .
Úlohou je zistiť, ako s využitím tohto grafu môžeme získať napríklad graf funkcie $g(x)= \frac{2}{x}$ ...
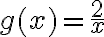Žiak by si mal uvedomiť, že platí vzťah 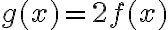$g(x)=2f(x)$ . Teda nad každý bod grafu funkcie ešte nanesieme jeho vzdialenosť od osi $o_x$ .
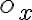Požadujeme od žiakov, aby vymenovali už známe vlastnosti funkcie nepriama úmernosť.

Lineárne lomená funkcia je každá funkcia na množine

$R ∖ \lbrace{\frac{-d}{c}}\rbrace$ , vyjadrená v tvare

$y= \frac{ax+b}{cx+d}$ ,
kde

$a,b,c,d$ sú reálne čísla,

$c \neq0$ a

$ad-bc \neq0$

Najprv žiaci riešia prípad lineárnej lomenej funkcie, 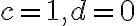Zlomok čiastočne skrátia a predpis funkcie upravia na tvar $y=a+ \frac{b}{x}$ .
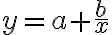Postupne žiaci prechádzajú aj k zložitejším zápisom funkcií. Pravdepodobne najprv budú skúšať zostrojiť graf na základe tabuľky, neskôr by mali prísť na to, ako nájdu stred hyperboly.
Veľmi častou chybou pri určovaní vlastností lomených funkcií je tvrdenie, že funkcia je klesajúca (resp. rastúca), pretože "graf funkcie stále klesá".
Žiak v tomto prípade nie celkom pochopil význam pojmu "klesajúca funkcia". Môže to byť spôsobené aj tým, že táto funkcii má bod nespojitosti.

$<span class="nolink">$ .$ $