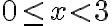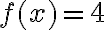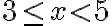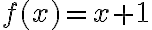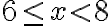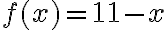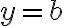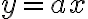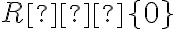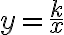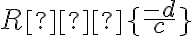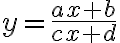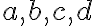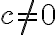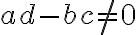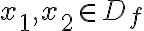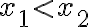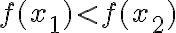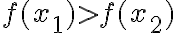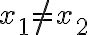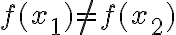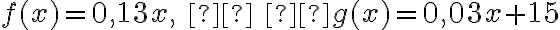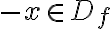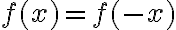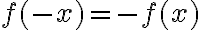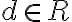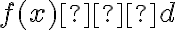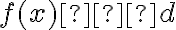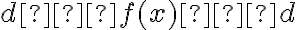Funkcie
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Funkcie |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:33 |
Opis
Funkcie
Vývoj a vznik pojmu funkcia
-
Predstavy o závislostiach javov v prírode pozorovali ľudia od „nepamäti“: Čím väčšie zviera sa uloví, tým viac ľudí sa nasýti, čím väčší oheň, tým viac tepla a pod.
Starovek
- Najstaršie dochované matematické poznatky o závislostiach čísel pochádzajú z Mezopotámie, Egypta, Indie a Číny.
- Veľkým pokrokom bolo uvedomenie si rozdielu medzi diskrétnou a súvislou veličinou, ktoré môžeme sledovať v antickom Grécku. Pytagorova škola skúmala vzťah medzi rôznymi fyzikálnymi veličinami - závislosť dĺžky struny na výške tónu.
- Arabská matematika – goniometrické funkcie, separované modely konkrétnych kriviek, univerzálny model všeobecnej krivky a jej extrémy.
- Okolo 12. až 14. storočia sa funkčné myslenie rozvíja aj v Európe. Začína sa vytvárať predstava o zákonoch prírody ako o zákonoch funkčného typu. Objavujú sa teórie zmeny veličiny ako funkcie času.
- Nicole Oresme (14. st.) vyjadroval veličiny a ich závislosti geometricky. Prvý používal termín funkčná závislosť.
Novovek: Matematika premenných veličín (17. st.). Bol definovaný pojem funkcie a následne vznikol diferenciálny a integrálny počet.
- René Descartes (1596 - 1650) zaviedol metódu súradníc: Číslo ↔ Poloha bodu.
- Gottfried Wilhelm Leibniz
(1646 - 1716) zaviedol symboliku, ktorá sa používa dodnes. Zaviedol pojem funkcia.
- Pojem funkcie vymedzil Leonhard Euler (1707 - 1783), ktorý vo svojom diele najprv definuje premennú a konštantnú veličinu a následne aj funkciu: "Funkcia premennej veličiny je analytický výraz zostavený akýmkoľvek spôsobom z tejto premennej veličiny a čísel alebo konštantných veličín."
- Nikolaj Ivanovič Lobačevskij a Peter Gustav L. Dirichlet zaviedli dnešné klasické poňatie funkcie ako jednoznačného priradenia.
- Neskôr vďaka teórii množín Richard Dedekind chápal funkciu ako zobrazenie jednej množiny do druhej.
_______________________________________________________________________________
1) HEJNÝ, Milan. Teória vyučovania matematiky.
2) Matematika v proměnách věků. Dějiny matematiky, svazek16.
3) The function concept. Tu
1) HEJNÝ, Milan. Teória vyučovania matematiky.
2) Matematika v proměnách věků. Dějiny matematiky, svazek16.
3) The function concept. Tu
Funkcie v školskej matematike
Pojem funkcie na základnej škole začíname propedeutikou
, ktorú prezentujú nasledujúce applety.
- Pri zavádzaní pojmu funkcia, učiteľ žiakom predloží predpis funkcie a pomocou niekoľkých bodov odvodí jej graf.
- Nasleduje zoznam vlastností a mnoho príkladov na precvičovanie.
- Pri zavádzaní pojmu funkcia je vhodné najprv žiakom pripomenúť niektoré im známe závislosti z reálneho života, vyjadrené predpisom alebo tabuľkou.
- objavujú kvantitatívne a priestorové vzťahy
- zoznámia sa s pojmom premennej veličiny a jej prvotnou reprezentáciou vo forme, tabuliek, grafov a diagramov
- skúmajú súvislostí, ktoré smerujú k zavedeniu pojmu funkcie
- objavujú kvantitatívne a priestorové vzťahy
- zoznámia sa s pojmom premennej veličiny a jej prvotnou reprezentáciou vo forme, tabuliek, grafov a diagramov
- skúmajú súvislostí, ktoré smerujú k zavedeniu pojmu funkcie
Applet umožňuje zadávať hodnoty nezávisle premennej
 do stĺpca A tabuľky napravo. Graf funkcie aktivujeme zaškrtnutím políčka v pravej dolnej časti appletu. Applet si stiahnite
Tu
.
do stĺpca A tabuľky napravo. Graf funkcie aktivujeme zaškrtnutím políčka v pravej dolnej časti appletu. Applet si stiahnite
Tu
.
Funkcie
na základnej škole
-
V ŠVP pre základné vzdelanie môžeme funkcie nájsť v tematickom okruhu Vzťahy, funkcie, tabuľky, diagramy. Žiaci:
Funkcie na strednej škole
-
Funkciám je venovaný tematický okruh Vzťahy, funkcie, tabuľky, diagramy, kde medzi učivom nájdeme aj postupnosti. Učivom sú v prvom rade všeobecné poznatky o funkciách, kam sa radí samotný pojem funkcie, definičný obor a obor hodnôt, graf
a vlastnosti funkcie. Ďalej sa preberajú jednotlivé elementárne funkcie (lineárna efektívna, absolútna hodnota, lineárne lomená, mocninové, druhá odmocnina, exponenciálne, logaritmické, goniometrické funkcie) a vzťahy medzi nimi. Žiaci:
________________________________________________________________
- 2) Vít Hejný; Milan Hejný Prečo je matematika taká ťažká?. Pokroky matematiky, fyziky a astronómie,Vol.23(1978),No.2,85--93 →
Pri spracovaní tejto sekcie boli použité texty z práce "Hanzalová: Funkce jedné proměnné na střední škole"1)
Poňatie funkcie jednej premennej v školskej matematike
Na základe historického vývoja pojmu funkcia postupne v školskej matematike sa vykryštalizovali tri základné poňatia pojmu funkcia
- Veličinové – závislosť premenných veličín (geometrických, fyzikálnych, ...)
- Množinové – priraďovanie medzi prvkami daných množín (pilierové na 1. st. ZŠ)
- Abstraktné – funkcia ako binárna relácia (číselné funkcie)
Na vhodných príkladoch závislostí medzi dvoma množinami 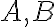 možno žiakom odvodiť pravidlo, že vždy jednému prvku množiny
možno žiakom odvodiť pravidlo, že vždy jednému prvku množiny  zodpovedá najviac jeden prvok množiny
zodpovedá najviac jeden prvok množiny 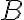 . Je vhodné pripomenúť, že naopak to neplatí. Napr. namerané teploty každú celú hodinu v jednom dni.
. Je vhodné pripomenúť, že naopak to neplatí. Napr. namerané teploty každú celú hodinu v jednom dni.
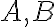 možno žiakom odvodiť pravidlo, že vždy jednému prvku množiny
možno žiakom odvodiť pravidlo, že vždy jednému prvku množiny  zodpovedá najviac jeden prvok množiny
zodpovedá najviac jeden prvok množiny 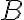 . Je vhodné pripomenúť, že naopak to neplatí. Napr. namerané teploty každú celú hodinu v jednom dni.
. Je vhodné pripomenúť, že naopak to neplatí. Napr. namerané teploty každú celú hodinu v jednom dni.
Funkcia na množine 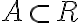 je predpis, ktorý každému číslu
je predpis, ktorý každému číslu 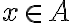 z množiny priraďuje práve jedno reálne číslo. Množina
z množiny priraďuje práve jedno reálne číslo. Množina  sa nazýva definičný obor.
sa nazýva definičný obor.
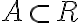 je predpis, ktorý každému číslu
je predpis, ktorý každému číslu 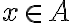 z množiny priraďuje práve jedno reálne číslo. Množina
z množiny priraďuje práve jedno reálne číslo. Množina  sa nazýva definičný obor.
sa nazýva definičný obor.
Zápis funkcie môže vyzerať napríklad nasledovne:
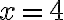 je
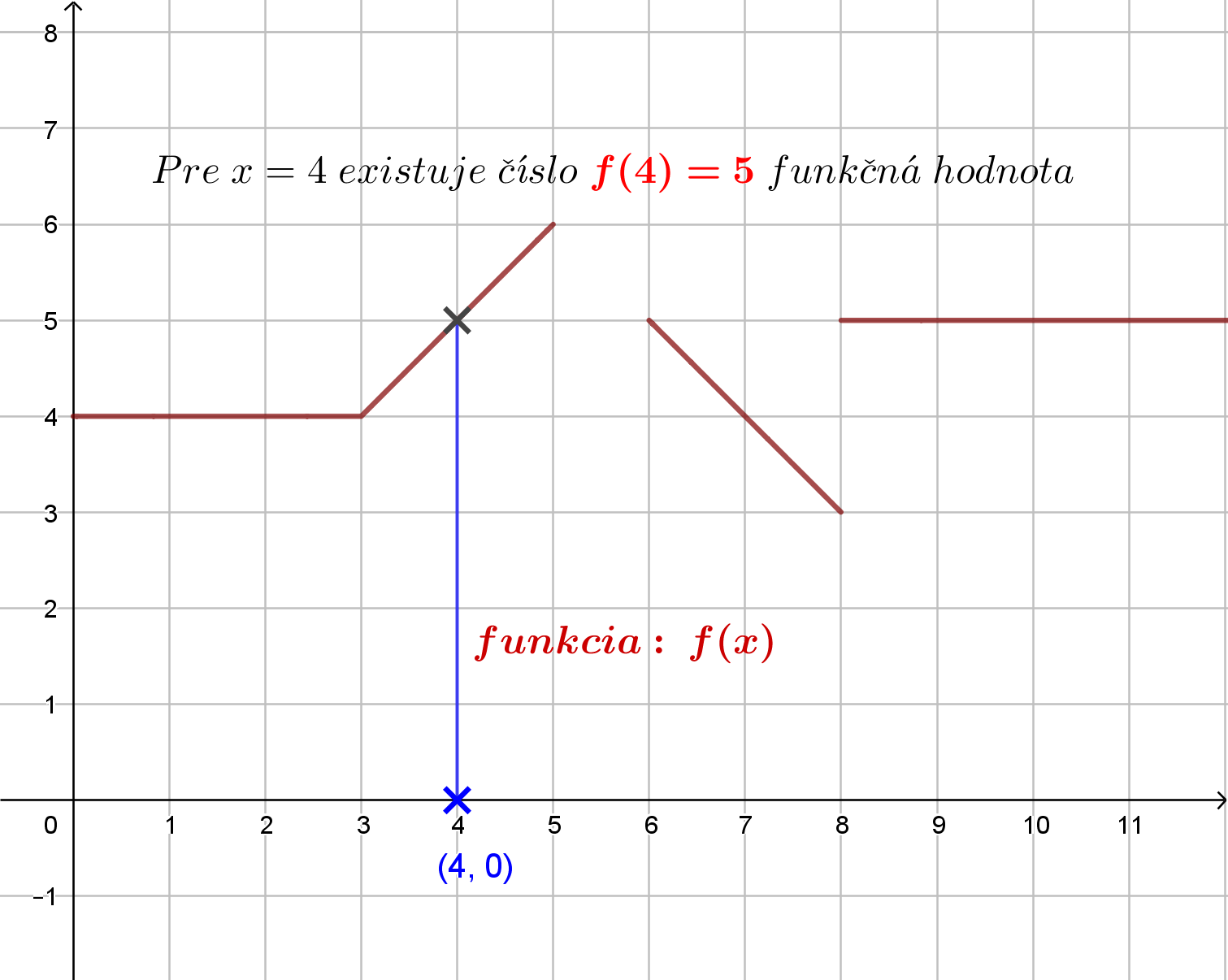
je 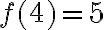 . Hovoríme: hodnota funkcie v bode 4 je rovná 5. Namiesto označenia hodnota funkcie budeme používať termín funkčná hodnota.
. Hovoríme: hodnota funkcie v bode 4 je rovná 5. Namiesto označenia hodnota funkcie budeme používať termín funkčná hodnota.
 →
→
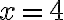 je
je 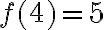 . Hovoríme: hodnota funkcie v bode 4 je rovná 5. Namiesto označenia hodnota funkcie budeme používať termín funkčná hodnota.
. Hovoríme: hodnota funkcie v bode 4 je rovná 5. Namiesto označenia hodnota funkcie budeme používať termín funkčná hodnota. →
→
Množinu všetkých funkčných hodnôt, ktoré funkcia v danom definičnom obore nadobúda, nazývame odbor hodnôt funkcie. Značíme ho symbolom 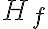
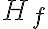
Poznámky.
Definičný obor označujeme ho symbolom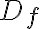 .
.
Odbor hodnôt funkcie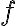 je množina všetkých
je množina všetkých 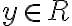 , ku ktorým existuje aspoň jedno
, ku ktorým existuje aspoň jedno  z definičného oboru funkcie
z definičného oboru funkcie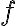 tak, že platí
tak, že platí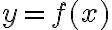 .
.
Pojmy závislosť, vzťah, priradenie, predpis nie sú matematicky definované pojmy. Používajú sa ako pomocné pojmy v rôznych intuitívnych významoch.
Matematicky vzťah medzi prvkami dvoch množín sa matematicky definuje ako binárna relácia medzi týmito množinami.
Definičný obor označujeme ho symbolom
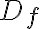 .
.
Odbor hodnôt funkcie
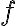 je množina všetkých
je množina všetkých 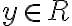 , ku ktorým existuje aspoň jedno
, ku ktorým existuje aspoň jedno  z definičného oboru funkcie
z definičného oboru funkcie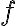 tak, že platí
tak, že platí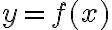 .
.
Pojmy závislosť, vzťah, priradenie, predpis nie sú matematicky definované pojmy. Používajú sa ako pomocné pojmy v rôznych intuitívnych významoch.
Matematicky vzťah medzi prvkami dvoch množín sa matematicky definuje ako binárna relácia medzi týmito množinami.
Príklad. Určte definičné obory a obory funkcií ... a vytvorte vhodný applet v prostredí GeoGebra.
Graf funkcie
Graf funkcie 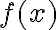 v euklidovskej rovine je množina všetkých bodov
v euklidovskej rovine je množina všetkých bodov ![[x, f(x)] [x, f(x)]](https://lms.umb.sk/filter/tex/pix.php/7c03b3d19da1c139f29d27ec3f5341ff.png) , kde
, kde  patrí do definičného oboru
patrí do definičného oboru 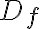 funkcie
funkcie 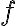 .
.
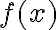 v euklidovskej rovine je množina všetkých bodov
v euklidovskej rovine je množina všetkých bodov ![[x, f(x)] [x, f(x)]](https://lms.umb.sk/filter/tex/pix.php/7c03b3d19da1c139f29d27ec3f5341ff.png) , kde
, kde  patrí do definičného oboru
patrí do definičného oboru 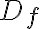 funkcie
funkcie 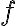 .
.
Žiaci zo základnej školy majú o grafoch určitú predstavu. Je však dôležité, aby si uvedomili, čo je pre graf funkcie charakteristické.
Ku grafom funkcií sa dajú priradiť nejaké závislosti z reálneho života.
- Napríklad zaznamenávanie nejakej fyzikálnej veličiny raz za určitú dobu - diskrétny graf
- Závislosť výšky hladiny vo vodnej nádrži v závislosti na čase - spojitý graf
Čo všetko môže žiak z grafu funkcie zistiť?
-
K jednotlivým hodnotám
 môže získať ich funkčnú hodnotu
môže získať ich funkčnú hodnotu 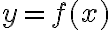 ako druhú súradnicu bodu
ako druhú súradnicu bodu ![X [x,y] X [x,y]](https://lms.umb.sk/filter/tex/pix.php/71312219fded8f1152294ebb448b012f.png)
-
K funkčným hodnotám
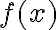 získame hodnoty
získame hodnoty  ako prvé súradnice bodu
ako prvé súradnice bodu ![X [x,y] X [x,y]](https://lms.umb.sk/filter/tex/pix.php/71312219fded8f1152294ebb448b012f.png) (môže existovať i nekonečne veľa).
(môže existovať i nekonečne veľa). -
Definičný obor určíme pomocou kolmých priemetov všetkých bodov grafu na os
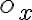 .
. -
Množinu všetkých funkčných hodnôt s využitím kolmých priemetov všetkých bodov grafu na os
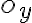 .
.
Príklad.
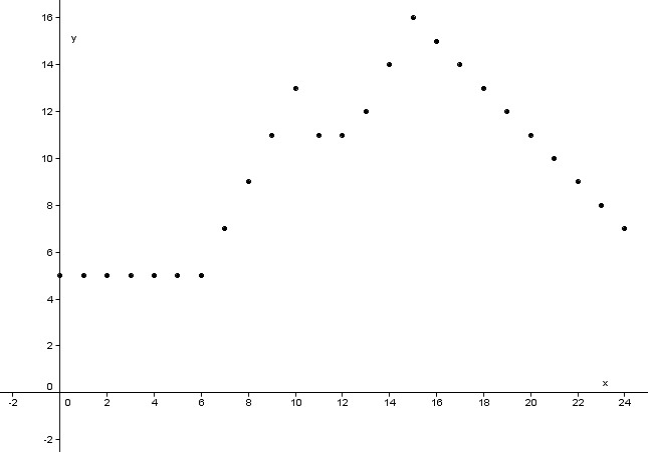
Načrtnite graf, ktorý ilustruje nasledujúcu situáciu:
Teplomer zapisuje nameranú teplotu každú hodinu. Petra zaujímal priebeh teploty 1. apríla. Hodnoty od polnoci až do šiestich do rána boli rovnaké, a to 5 ° C. Následne každú hodinu teplota vzrástla o dva stupne až do desiatej hodín (vrátane). Potom však začalo pršať a teplota v jedenásť hodín klesla až do dvanástich na 11 ° C. V jednu popoludní dážď ustal a začalo svietiť slnko. To spôsobilo opäť oteplenie. V jednu hodinu bolo už 12 ° C, a následne do troch hodín vždy teplota vzrástla o dva stupne. Potom teplota už len klesala vždy každú hodinu o jeden stupeň.
Elementárne funkcie
S funkciami majú žiaci skúsenosti už zo základnej školy, kde sa preberá priama úmernosť.
Začnime motivačnou úlohou:
- V obchode prebieha akcia. Cena jedného kg banánov je teraz za 0,75 EUR. Pri jednom nákupe je možné kúpiť akékoľvek množstvo do 15 kg. Zakreslite graf závislosti ceny banánov na množstve (vyberte vhodné jednotky na osi a) a zapíšte predpis funkcie, ktorá túto závislosť popisuje.
- Z grafu vyčítajte, koľko bude zákazníka stáť 5 resp. 8 kg banánov a koľko kg si zákazník kúpi za 3 EUR.
- Narysujte graf a zapíšte predpis funkcie charakterizujúce situáciu, kedy sa cena banánov zvýšila o 0,4 EUR. Ako sa tento graf zmenil oproti pôvodnému? Aké následky by malo zníženie ceny banánov oproti pôvodnej cene - svoju úvahu overte na príklade.
- Diskutujte, ako by sa graf menil pri rôznych zmenách ceny banánov.
V tejto úlohe sa žiak zoznámi s konkrétnymi predpismi a grafmi lineárnych funkcií na definičnom obore.
Seminárne cvičenie
Navrhnite vzorové riešenie tejto úlohy pre žiakov ZŠ.
Vytvorte v prostredí GeoGebra graf funkcie, v ktorom bude možné meniť cenu banánov a množstvo nakúpených banánov.
Vytvorte v prostredí GeoGebra graf funkcie, v ktorom bude možné meniť cenu banánov a množstvo nakúpených banánov.
Lineárna funkcia
Lineárna funkcia
je každá funkcia definovaná na množine reálnych čísel, ktorá je daná v tvare
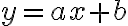 kde
kde
 sú reálne čísla.
sú reálne čísla.
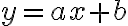 kde
kde
 sú reálne čísla.
sú reálne čísla.
Už v motivačných príkladoch na ZŠ je vhodné zahrnúť prácu s grafom resp. s časťou lineárneho grafu. Žiaci:
Pozri GeoGebra knihu: Adriana Šudiová, Lineárna funkcia Tu , applet Cesta autom 1, upravené Tu, applet Bazén Tu
Úloha. Upravte ďalšie applety z knihy Lineárna funkcia od A. Šudiovej.
Riešte slovné úlohy (Polák, str.86-87) ktoré interpretujú lineárnu funkciu. Vytvorte k nim vhodné applety .
Kvadratická funkcia
Kvadratická funkcia je každá funkcia definovaná na množine reálnych čísel, ktorá má tvar:
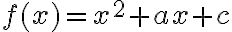
kde koeficienty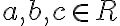 pričom
pričom 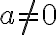 . Pozri aktivitu GeoGebra Tu
. Pozri aktivitu GeoGebra Tu
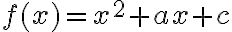
kde koeficienty
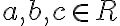 pričom
pričom 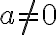 . Pozri aktivitu GeoGebra Tu
. Pozri aktivitu GeoGebra Tu
S týmto predpisom žiakov zoznámime zadaním niekoľkých separovaných modelov, kde budú rôzne koeficienty
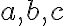 .
.
Tie by mali zahŕňať aj prípady, keď je záporné číslo,
je záporné číslo,  je rovné nule alebo
je rovné nule alebo  je rovné nule.
je rovné nule.
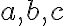 a určitým umiestnením grafu.
a určitým umiestnením grafu.
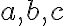 .
. Tie by mali zahŕňať aj prípady, keď
 je záporné číslo,
je záporné číslo,  je rovné nule alebo
je rovné nule alebo  je rovné nule.
je rovné nule. - Žiaci načrtnú grafy svojich zadaných funkcií a nasleduje diskusia v triede.
Všetkým žiakom vyjde parabola, zakaždým však umiestnená iným spôsobom.
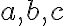 a určitým umiestnením grafu.
a určitým umiestnením grafu.
Grafom kvadratickej funkcie je vždy parabola, ktorá je súmerná podľa osi rovnobežnej s osou
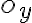 . Ak je:
. Ak je:
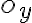 . Ak je:
. Ak je:- koeficient
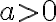 , ide o funkciu zdola ohraničenú[, minimum má vo vrchole paraboly
, ide o funkciu zdola ohraničenú[, minimum má vo vrchole paraboly
![V[- \frac{b}{2a}, c -\frac{b^2}{4a}] V[- \frac{b}{2a}, c -\frac{b^2}{4a}]](https://lms.umb.sk/filter/tex/pix.php/c829efcae5e239f18dcc68f53c5efe89.png)
- koeficient
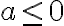 , ide o funkciu zhora ohraničenú a maximum má opäť vo vrchole paraboly
, ide o funkciu zhora ohraničenú a maximum má opäť vo vrchole paraboly - pozrite si algebraické výpočty (CAS) v GeoGebre, Príklad 2 Tu
Tvar kvadratickej funkcie možno previesť na tvar
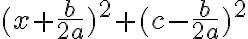 ,
,
z ktorého ľahko určíme súradnice vrcholu paraboly.
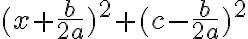 ,
,z ktorého ľahko určíme súradnice vrcholu paraboly.
Príklad. Hospodár chce vytvoriť obdĺžnikovú ohradu. K dispozícii má 36 m pletiva. Aké musia byť rozmery obdĺžnika, aby ohrada ohraničovala čo najväčšiu časť pozemku?
Pozri aktivitu Kvadratická funkcia 1, Autor: Štefan Havrlent, Tu
Grafy kvadratických funkcií sa dajú využiť aj pri riešení kvadratických nerovníc alebo pri sústavách rovníc a nerovníc, v ktorých sa kvadratická funkcia vyskytuje.
Lineárna lomená funkcia
Žiaci by už mali byť oboznámení s funkciou nepriama úmernosť, preto je vhodné použiť nejaký motivačný príklad tohto špecifického prípadu lomenej funkcie
Vyhľadajte aktivity v GeoGebre, napríklad Lineárna lomená funkcia (František Legát)
Grafom nepriamej úmernosti je krivka, ktorá sa nazýva rovnoosá hyperbola.
-
Najskôr zostrojíme graf funkcie
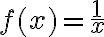 , ktorý možno zostrojiť na základe tabuľky s dostatočným počtom rôznych hodnôt pre
, ktorý možno zostrojiť na základe tabuľky s dostatočným počtom rôznych hodnôt pre  .
. - Úlohou je zistiť, ako s využitím tohto grafu môžeme získať napríklad graf funkcie
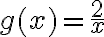 ...
... - Žiak by si mal uvedomiť, že platí vzťah
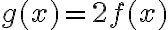 . Teda nad každý bod grafu funkcie ešte nanesieme jeho vzdialenosť od osi
. Teda nad každý bod grafu funkcie ešte nanesieme jeho vzdialenosť od osi 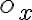 .
. - Požadujeme od žiakov, aby vymenovali už známe vlastnosti funkcie nepriama úmernosť.
- Najprv žiaci riešia prípad lineárnej lomenej funkcie,
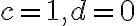 . Zlomok čiastočne skrátia a predpis funkcie upravia na tvar
. Zlomok čiastočne skrátia a predpis funkcie upravia na tvar 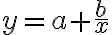 .
. - Postupne žiaci prechádzajú aj k zložitejším zápisom funkcií. Pravdepodobne najprv budú skúšať zostrojiť graf na základe tabuľky, neskôr by mali prísť na to, ako nájdu stred hyperboly.
- Veľmi častou chybou pri určovaní vlastností lomených funkcií je tvrdenie, že funkcia je klesajúca (resp. rastúca), pretože "graf funkcie stále klesá".
- Žiak v tomto prípade nie celkom pochopil význam pojmu "klesajúca funkcia". Môže to byť spôsobené aj tým, že táto funkcii má bod nespojitosti.
Špecifické vlastnosti funkcií, operácie s funkciami
Súčasťou tematického celku Funkcie na SŠ je aj oboznámenie žiakov s vlastnosťami (druhy funkcií):
- Monotónnosť funkcie - (ne)rastúca a (ne)klesajúca funkcia
- Prostá funkcia, ohraničená funkcia
- Párna a nepárna funkcia, periodická funkcia
- Zložená funkcia
Dôležitý je aj pojem rastúca (resp. klesajúca) funkcia v danom intervale. K tomu môžeme použiť graf funkcie, ktorý na určitom intervale "rastie", na inom intervale "klesá".
• Navrhnite príklady, v ktorých žiaci majú za úlohu zistiť, či ide o funkciu rastúcu alebo klesajúcu na danom intervale.
• Očakávaná odpoveď: Pre všetky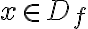 nie je ani rastúca ani klesajúca ale na intervale je ...
nie je ani rastúca ani klesajúca ale na intervale je ...
Zavádzame pojmy: monotónna funkcia, rýdzo monotónna ...
• Navrhnite príklady, v ktorých žiaci majú za úlohu zistiť, či ide o funkciu rastúcu alebo klesajúcu na danom intervale.
• Očakávaná odpoveď: Pre všetky
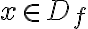 nie je ani rastúca ani klesajúca ale na intervale je ...
nie je ani rastúca ani klesajúca ale na intervale je ... Zavádzame pojmy: monotónna funkcia, rýdzo monotónna ...
Prostá funkcia
S týmto pojmom by si mali žiaci spojiť rozdiel medzi konštantnými a s lineárnymi funkciami, pre ktoré je 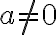 .
.
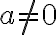 .
.
Príklad
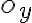 (cena). Teda v intervale 〈0,100〉 je pre zákazníka výhodnejšie tarifu T0 a od 100 minút vyššie je výhodnejšie tarifa T150.
(cena). Teda v intervale 〈0,100〉 je pre zákazníka výhodnejšie tarifu T0 a od 100 minút vyššie je výhodnejšie tarifa T150.
 →
→
Mobilný operátor ponúka dva tarify T150 a T0. Pre tarifa T0 nie je nutné zaplatiť mesačný paušál a za minútu telefonovanie zaplatíme 0,13 €/min. Pre tarifa T150 musíme mesačne zaplatiť 15 € a za každú minútu telefonovanie zaplatíme 0,06 €/min. Určte, prie koľkých mesačne prevolaných minútach je výhodnejšie tarifa T0.
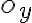 (cena). Teda v intervale 〈0,100〉 je pre zákazníka výhodnejšie tarifu T0 a od 100 minút vyššie je výhodnejšie tarifa T150.
(cena). Teda v intervale 〈0,100〉 je pre zákazníka výhodnejšie tarifu T0 a od 100 minút vyššie je výhodnejšie tarifa T150. →
→Ďalšie vlastnosti
Opäť je vhodné uvádzať konkrétne príklady takýchto funkcií: priemerná rýchlosť automobilu v závislosti na čase alebo teplota v závislosti na čase.
So žiakmi by sa malo diskutovať, či už poznajú nejaký konkrétny predpis ohraničenej funkcie.
So žiakmi by sa malo diskutovať, či už poznajú nejaký konkrétny predpis ohraničenej funkcie.
Navrhnite definície vhodné pre SŠ:
• periodická funkcia • zložená funkcia • rovnosť funkcií • inverzná funkcia • maximum, minimum • algebraické operácie pre funkcie
• periodická funkcia • zložená funkcia • rovnosť funkcií • inverzná funkcia • maximum, minimum • algebraické operácie pre funkcie
Navrhnite úlohy pre SŠ, ktoré budú interpretovať tieto vlastnosti funkcií. Vytvorte k nim vhodné applety