Komplexné čísla na strednej škole
Komplexné čísla na strednej škole
Zobrazenie množiny všetkých komplexných čísel 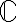 na množinu bodov euklidovskej roviny
na množinu bodov euklidovskej roviny 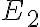 je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.
je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.
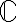 na množinu bodov euklidovskej roviny
na množinu bodov euklidovskej roviny 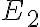 je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.
je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.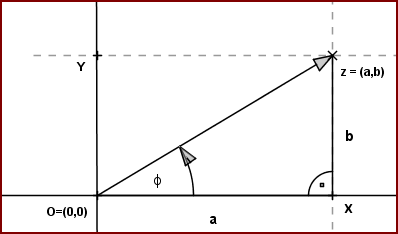
Z definície goniometrických funkcií sínus a kosínus vyplýva , že platia rovnosti:
(1) sin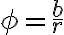 , cos
, cos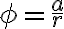 ,
,
kde![r= \sqrt[]{a^2+b^2} r= \sqrt[]{a^2+b^2}](https://lms.umb.sk/filter/tex/pix.php/3dc55d8a6ad1e8caa1e3b68c6e862d1e.png) a
a
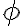 je orientovaný uhol ∢XOZ.
je orientovaný uhol ∢XOZ.
(1) sin
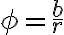 , cos
, cos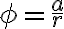 ,
, kde
![r= \sqrt[]{a^2+b^2} r= \sqrt[]{a^2+b^2}](https://lms.umb.sk/filter/tex/pix.php/3dc55d8a6ad1e8caa1e3b68c6e862d1e.png) a
a
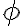 je orientovaný uhol ∢XOZ.
je orientovaný uhol ∢XOZ.
Číslo
 predstavuje veľkosť vektora
predstavuje veľkosť vektora
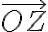 . Na základe definície absolútnej hodnoty
. Na základe definície absolútnej hodnoty 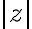 komplexného čísla
komplexného čísla 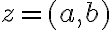 platí
platí ![|z|= \sqrt[]{a^2+b^2 } |z|= \sqrt[]{a^2+b^2 }](https://lms.umb.sk/filter/tex/pix.php/573976f8bded85cf312bf40c882f9559.png) . Odkiaľ dostávame, že
. Odkiaľ dostávame, že 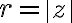 .
.
Z rovností (1) môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla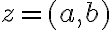 . Dostaneme
. Dostaneme
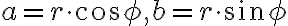
Vypočítané hodnoty môžeme dosadiť do algebrického tvaru komplexného čísla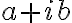 .
Dostaneme zápis resp. nový tvar komplexného čísla
.
Dostaneme zápis resp. nový tvar komplexného čísla
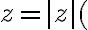 cos
cos 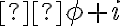 sin
sin 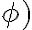
ktorý nazývame goniometrický tvar komplexného čísla.
 predstavuje veľkosť vektora
predstavuje veľkosť vektora
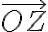 . Na základe definície absolútnej hodnoty
. Na základe definície absolútnej hodnoty 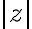 komplexného čísla
komplexného čísla 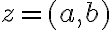 platí
platí ![|z|= \sqrt[]{a^2+b^2 } |z|= \sqrt[]{a^2+b^2 }](https://lms.umb.sk/filter/tex/pix.php/573976f8bded85cf312bf40c882f9559.png) . Odkiaľ dostávame, že
. Odkiaľ dostávame, že 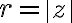 .
.Z rovností (1) môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
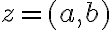 . Dostaneme
. Dostaneme
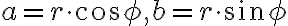
Vypočítané hodnoty môžeme dosadiť do algebrického tvaru komplexného čísla
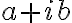 .
Dostaneme zápis resp. nový tvar komplexného čísla
.
Dostaneme zápis resp. nový tvar komplexného čísla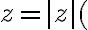 cos
cos 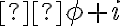 sin
sin 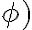
ktorý nazývame goniometrický tvar komplexného čísla.
