Komplexné čísla na strednej škole
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Komplexné čísla na strednej škole |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 11:24 |
Opis
Komplexné čísla na strednej škole
Motivačným zdrojom pre zavedenie oboru komplexných čísel je "neriešiteľnosť" rovnice 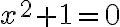 . Žiakom už na ZŠ by sme mali odôvodniť, že
. Žiakom už na ZŠ by sme mali odôvodniť, že
Súčet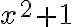 pre ľubovoľné reálne číslo
pre ľubovoľné reálne číslo 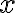 vždy bude kladné číslo
vždy bude kladné číslo
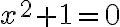 . Žiakom už na ZŠ by sme mali odôvodniť, že
. Žiakom už na ZŠ by sme mali odôvodniť, že
Súčet
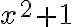 pre ľubovoľné reálne číslo
pre ľubovoľné reálne číslo 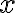 vždy bude kladné číslo
vždy bude kladné číslo
Preto rovnica 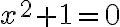 nemá v obore reálnych čísel riešenie
nemá v obore reálnych čísel riešenie
Na SŠ sa často použije formulácia: Číslo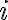 definujeme ako riešenie takejto rovnice. Nech
definujeme ako riešenie takejto rovnice. Nech 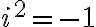 , potom ...
, potom ...
Vhodnejšie by bola formulácia typu: Na chvíľu si predstavme, že také číslo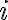 už máme. Nech platí
už máme. Nech platí 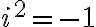 , potom ...
, potom ...
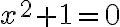 nemá v obore reálnych čísel riešenie
nemá v obore reálnych čísel riešenie
Na SŠ sa často použije formulácia: Číslo
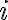 definujeme ako riešenie takejto rovnice. Nech
definujeme ako riešenie takejto rovnice. Nech 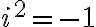 , potom ...
, potom ...
Vhodnejšie by bola formulácia typu: Na chvíľu si predstavme, že také číslo
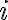 už máme. Nech platí
už máme. Nech platí 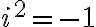 , potom ...
, potom ...
Historický rámec zavedenia pojmu komplexného čísla
- Motivačným zdrojom pre zavedenie oboru komplexných čísel nebol problém riešenia kvadratickej rovnice so záporným diskriminantom.
- Podnetom bol iný problém: algebraické riešenie kubických rovníc.
Kubická rovnica
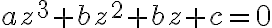 sa po substitúcii
sa po substitúcii
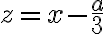 redukuje na tvar
redukuje na tvar
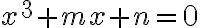 (14.st., Florencia).
(14.st., Florencia).
Potom stačí uvažovať o troch typoch kubických rovníc: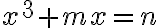 ,
,
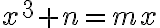 a
a
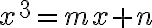 , kde
, kde
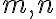 sú kladné koeficienty.
sú kladné koeficienty.
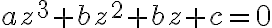 sa po substitúcii
sa po substitúcii
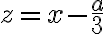 redukuje na tvar
redukuje na tvar
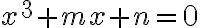 (14.st., Florencia).
(14.st., Florencia).
Potom stačí uvažovať o troch typoch kubických rovníc:
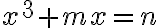 ,
,
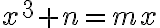 a
a
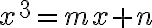 , kde
, kde
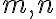 sú kladné koeficienty.
sú kladné koeficienty.
Kubickú rovnicu
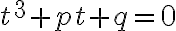 môžeme riešiť
môžeme riešiť
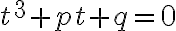 môžeme riešiť
môžeme riešiť
- substitúciou
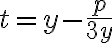 , ktorú použil Thomas Harriot (1560-1621)
, ktorú použil Thomas Harriot (1560-1621) - dostaneme rovnicu šiesteho stupňa, ktorá po úprave vedie k riešeniu
- alebo originál Cardanovou metódou, pozri Wikipédiu. Genialita Cardanovho riešenia spočíta v zavedení
Rovnica 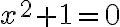 nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor
nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor 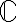 , kde rovnice tohto typu budú mať riešenie.
, kde rovnice tohto typu budú mať riešenie.
Budeme požadovať, aby existovalo nejaké „imaginárne “ číslo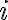 , pre ktoré je druhá mocnina rovná
, pre ktoré je druhá mocnina rovná 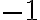 .
.
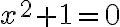 nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor
nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor 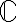 , kde rovnice tohto typu budú mať riešenie.
, kde rovnice tohto typu budú mať riešenie. Budeme požadovať, aby existovalo nejaké „imaginárne “ číslo
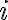 , pre ktoré je druhá mocnina rovná
, pre ktoré je druhá mocnina rovná 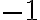 .
.
Predstavme si, že také číslo 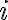 už máme. Nech platí
už máme. Nech platí
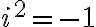 , potom zrejme bude platiť aj rovnosť
, potom zrejme bude platiť aj rovnosť
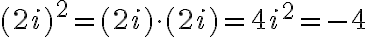 resp. pre ľubovoľné reálne číslo
resp. pre ľubovoľné reálne číslo  bude
bude
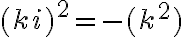 . Čísla
. Čísla
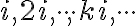 nie sú reálne. Nazveme ich „imaginárne čísla“.
nie sú reálne. Nazveme ich „imaginárne čísla“.
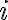 už máme. Nech platí
už máme. Nech platí
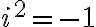 , potom zrejme bude platiť aj rovnosť
, potom zrejme bude platiť aj rovnosť
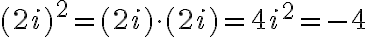 resp. pre ľubovoľné reálne číslo
resp. pre ľubovoľné reálne číslo  bude
bude
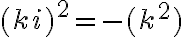 . Čísla
. Čísla
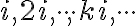 nie sú reálne. Nazveme ich „imaginárne čísla“.
nie sú reálne. Nazveme ich „imaginárne čísla“.
Pri vytváraní číselného oboru 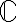 budeme požadovať, aby
budeme požadovať, aby
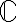 budeme nazývať komplexné čísla a budeme ich zapisovať v tvare
budeme nazývať komplexné čísla a budeme ich zapisovať v tvare 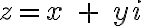 .
.
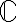 budeme požadovať, aby
budeme požadovať, aby
-
všetky súčty
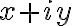 , kde
, kde 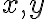 sú ľubovoľné reálne čísla, patrili opäť do oboru
sú ľubovoľné reálne čísla, patrili opäť do oboru 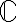
-
dva prvky
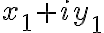 ,
, 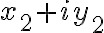 sa rovnali práve vtedy, keď
sa rovnali práve vtedy, keď 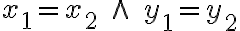
- boli vhodne definované operácie sčítania a násobenia
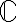 budeme nazývať komplexné čísla a budeme ich zapisovať v tvare
budeme nazývať komplexné čísla a budeme ich zapisovať v tvare 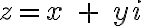 .
.
Reálne číslo
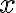 sa nazýva reálna časť komplexného čísla
sa nazýva reálna časť komplexného čísla
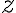 a označujeme ju symbolom
a označujeme ju symbolom
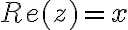
Reálne číslo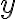 sa nazýva imaginárna časť komplexného čísla
sa nazýva imaginárna časť komplexného čísla
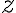 a označujeme ju symbolom
a označujeme ju symbolom
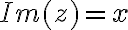
Opačné číslo ku komplexnému číslu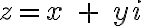 je komplexné číslo
je komplexné číslo
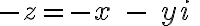
Komplexne združené číslo ku komplexnému číslu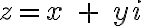 je komplexné číslo
je komplexné číslo 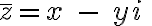
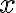 sa nazýva reálna časť komplexného čísla
sa nazýva reálna časť komplexného čísla
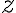 a označujeme ju symbolom
a označujeme ju symbolom
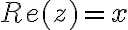
Reálne číslo
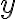 sa nazýva imaginárna časť komplexného čísla
sa nazýva imaginárna časť komplexného čísla
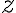 a označujeme ju symbolom
a označujeme ju symbolom
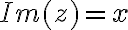
Opačné číslo ku komplexnému číslu
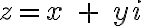 je komplexné číslo
je komplexné číslo
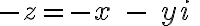
Komplexne združené číslo ku komplexnému číslu
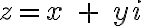 je komplexné číslo
je komplexné číslo 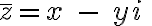
Pri zavádzaní komplexných čísel prevažujú tri typy metodického spracovania
- Tradičné poňatie je založené na adjunkcii (pridaní) imaginárnej jednotky
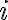 k oboru reálnych čísel - staršie učebnice matematiky, O. Petránek (1985), B. Riečan (1987)
k oboru reálnych čísel - staršie učebnice matematiky, O. Petránek (1985), B. Riečan (1987) - Modelové poňatie oboru komplexných čísel vychádza z množiny usporiadaných dvojíc, na ktorej sú vhodne definované operácie sčítania a násobenia - E. Čech (1951)
- Kombinované poňatie spočíva v didakticky vhodnom prepojení obidvoch predchádzajúcich poňatí - J. Kabele (1961), novšie učebnice matematiky
Výhody a nevýhody
- Pri tradičnom poňatí sa vychádza z nezaručeného predpokladu existencie takéhoto rozšíreného oboru reálnych čísel. Komplexné čísla sa zavádzajú v algebraickom tvare
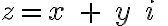 . Existencia oboru sa zaistí pomocou aritmetického modelu, v ktorom komplexné čísla sú reprezentované usporiadanými dvojicami
. Existencia oboru sa zaistí pomocou aritmetického modelu, v ktorom komplexné čísla sú reprezentované usporiadanými dvojicami
![[x,y] [x,y]](https://lms.umb.sk/filter/tex/pix.php/08ed78fbb24c631f7137cceeee6e4402.png) reálnych čísel. Definitoricky sa položí
reálnych čísel. Definitoricky sa položí
![[x,y] =x+yi [x,y] =x+yi](https://lms.umb.sk/filter/tex/pix.php/90df92633d1a36af8e4b2008a779cf77.png) .
. - Pri zavedení komplexných čísel ako usporiadaných dvojíc je didaktickým problémom "absence motivace definice sučinu"1) komplexných čísel.
- Kombinované poňatie je založené na postupných krokoch
______________________________________________________
1) Polák, J.: Didaktika matematiky
1) Polák, J.: Didaktika matematiky
Vlastnosti absolútnej hodnoty
Vlastnosti operácií sčítania a násobenia
- Pre súčet a súčin komplexných čísel platí vlastnosť komutatívnosti a asociatívnosti, pričom súčin je distributívny k sčítaniu.
- Neutrálny (nulový) prvok pre sčítanie je komplexné číslo (0, 0).
- Neutrálny (jednotkový) prvok pre násobenie je komplexné číslo (1, 0).
- K ľubovoľnému komplexnému číslu
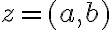 existuje inverzný prvok
existuje inverzný prvok
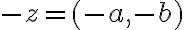 vzhľadom na sčítanie. Takýto prvok budeme nazývať opačné komplexné číslo.
vzhľadom na sčítanie. Takýto prvok budeme nazývať opačné komplexné číslo. -
K ľubovoľnému nenulovému komplexnému číslu
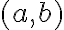 existuje inverzný prvok
existuje inverzný prvok 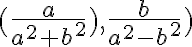 vzhľadom na súčin. Budeme ho označovať symbolom
vzhľadom na súčin. Budeme ho označovať symbolom 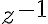 .
.
Navrhnite dôkazy týchto tvrdení vhodné pre žiakov na strednej škole.
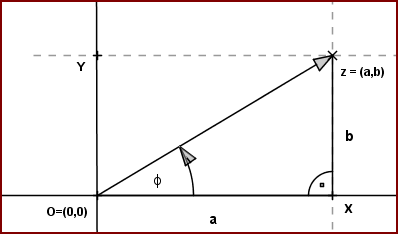
Zobrazenie množiny všetkých komplexných čísel 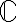 na množinu bodov euklidovskej roviny
na množinu bodov euklidovskej roviny  je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.
je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.
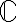 na množinu bodov euklidovskej roviny
na množinu bodov euklidovskej roviny 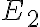 je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.
je vzájomne jednoznačné. Táto rovina sa potom nazýva Gaussova rovina.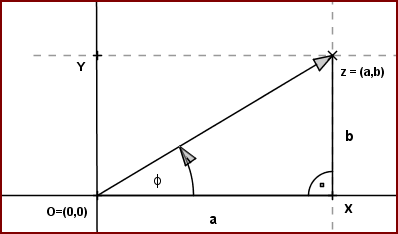
Z definície goniometrických funkcií sínus a kosínus vyplýva , že platia rovnosti:
(1) sin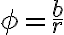 , cos
, cos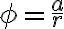 ,
,
kde![r= \sqrt[]{a^2+b^2} r= \sqrt[]{a^2+b^2}](https://lms.umb.sk/filter/tex/pix.php/3dc55d8a6ad1e8caa1e3b68c6e862d1e.png) a
a
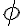 je orientovaný uhol ∢XOZ.
je orientovaný uhol ∢XOZ.
(1) sin
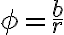 , cos
, cos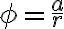 ,
, kde
![r= \sqrt[]{a^2+b^2} r= \sqrt[]{a^2+b^2}](https://lms.umb.sk/filter/tex/pix.php/3dc55d8a6ad1e8caa1e3b68c6e862d1e.png) a
a
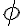 je orientovaný uhol ∢XOZ.
je orientovaný uhol ∢XOZ.
Číslo
 predstavuje veľkosť vektora
predstavuje veľkosť vektora
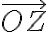 . Na základe definície absolútnej hodnoty
. Na základe definície absolútnej hodnoty 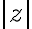 komplexného čísla
komplexného čísla 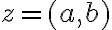 platí
platí ![|z|= \sqrt[]{a^2+b^2 } |z|= \sqrt[]{a^2+b^2 }](https://lms.umb.sk/filter/tex/pix.php/573976f8bded85cf312bf40c882f9559.png) . Odkiaľ dostávame, že
. Odkiaľ dostávame, že 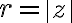 .
.
Z rovností (1) môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla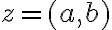 . Dostaneme
. Dostaneme
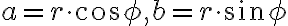
Vypočítané hodnoty môžeme dosadiť do algebrického tvaru komplexného čísla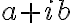 .
Dostaneme zápis resp. nový tvar komplexného čísla
.
Dostaneme zápis resp. nový tvar komplexného čísla
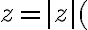 cos
cos 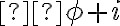 sin
sin 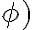
ktorý nazývame goniometrický tvar komplexného čísla.
 predstavuje veľkosť vektora
predstavuje veľkosť vektora
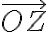 . Na základe definície absolútnej hodnoty
. Na základe definície absolútnej hodnoty 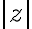 komplexného čísla
komplexného čísla 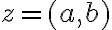 platí
platí ![|z|= \sqrt[]{a^2+b^2 } |z|= \sqrt[]{a^2+b^2 }](https://lms.umb.sk/filter/tex/pix.php/573976f8bded85cf312bf40c882f9559.png) . Odkiaľ dostávame, že
. Odkiaľ dostávame, že 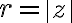 .
.Z rovností (1) môžeme vyjadriť reálnu aj imaginárnu zložku komplexného čísla
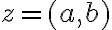 . Dostaneme
. Dostaneme
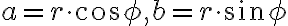
Vypočítané hodnoty môžeme dosadiť do algebrického tvaru komplexného čísla
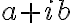 .
Dostaneme zápis resp. nový tvar komplexného čísla
.
Dostaneme zápis resp. nový tvar komplexného čísla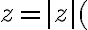 cos
cos 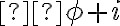 sin
sin 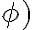
ktorý nazývame goniometrický tvar komplexného čísla.
Každé reálne číslo 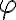 , ktoré vyhovuje rovniciam (1) nazývame hodnota argumentu komplexného čísla
, ktoré vyhovuje rovniciam (1) nazývame hodnota argumentu komplexného čísla 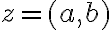 .
.
Pre komplexné číslo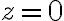 nie je definovaná žiadna hodnota argumentu.
nie je definovaná žiadna hodnota argumentu.
Z periodickosti funkcií sínus a kosínus vyplýva, že každé nenulové komplexné číslo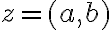 má nekonečne veľa hodnôt argumentu.
má nekonečne veľa hodnôt argumentu.
Ak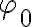 je jedna z nich, potom všetky ostatné sa dajú vyjadriť v tvare
je jedna z nich, potom všetky ostatné sa dajú vyjadriť v tvare 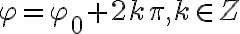 .
.
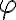 , ktoré vyhovuje rovniciam (1) nazývame hodnota argumentu komplexného čísla
, ktoré vyhovuje rovniciam (1) nazývame hodnota argumentu komplexného čísla 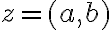 .
. Pre komplexné číslo
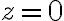 nie je definovaná žiadna hodnota argumentu.
nie je definovaná žiadna hodnota argumentu. Z periodickosti funkcií sínus a kosínus vyplýva, že každé nenulové komplexné číslo
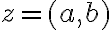 má nekonečne veľa hodnôt argumentu.
má nekonečne veľa hodnôt argumentu. Ak
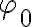 je jedna z nich, potom všetky ostatné sa dajú vyjadriť v tvare
je jedna z nich, potom všetky ostatné sa dajú vyjadriť v tvare 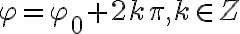 .
.Množinu reálnych čísel 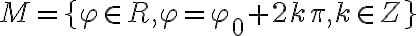 nazývame argument komplexného čísla
nazývame argument komplexného čísla 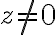 .
.
Množinu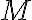 budeme označovať symbolom Arg
budeme označovať symbolom Arg 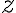 .
.
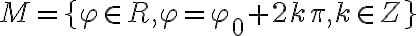 nazývame argument komplexného čísla
nazývame argument komplexného čísla 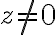 .
. Množinu
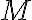 budeme označovať symbolom Arg
budeme označovať symbolom Arg 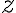 .
.
Tú z hodnôt argumentu, pre ktorú platí 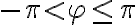 , nazývame hlavná hodnota argumentu komplexného čísla
, nazývame hlavná hodnota argumentu komplexného čísla 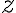 a označujeme arg
a označujeme arg 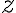 .
.
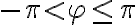 , nazývame hlavná hodnota argumentu komplexného čísla
, nazývame hlavná hodnota argumentu komplexného čísla 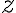 a označujeme arg
a označujeme arg 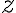 .
.
Poznámka
Na strednej škole je veľmi dôležité neustále zdôrazňovať žiakom, že hodnôt argumentu komplexného čísla je nekonečne veľa.
Na strednej škole je veľmi dôležité neustále zdôrazňovať žiakom, že hodnôt argumentu komplexného čísla je nekonečne veľa.
Francúzsky matematik Abraham de Moivre sformuloval vetu, podľa ktorej môžeme jednoducho umocňovať komplexné čísla vyjadrené v goniometrickom tvare.
Z Moivreovej vety vyplýva aj jej odvodený tvar pre súčin dvoch komplexných čísel.
Poznámky
Dôležité je uvedomiť si, že komplexnými číslami končí rozširovanie číselného oboru.
V roku 1799 Gauss dokázal, že každá algebraická rovnica, ktorej koeficienty sú komplexné čísla, má v obore komplexných čísel riešenie. To znamená, že obor komplexných čísel už nie je potrebné ďalej rozširovať.
Odmocnina komplexného čísla: Jarník, Jiří: Komplexní čísla a funkce. Praha: Mladá fronta, 1967. Dostupné na Czech Digital Mathematics Library Tu
V roku 1799 Gauss dokázal, že každá algebraická rovnica, ktorej koeficienty sú komplexné čísla, má v obore komplexných čísel riešenie. To znamená, že obor komplexných čísel už nie je potrebné ďalej rozširovať.
Odmocnina komplexného čísla: Jarník, Jiří: Komplexní čísla a funkce. Praha: Mladá fronta, 1967. Dostupné na Czech Digital Mathematics Library Tu
Vytvorte samostatné prezentácie na témy
Využitie komplexných
čísel pri riešení úloh
Binomická veta a jej
využitie pri riešení úloh
Cardanove vzorce a ich
využitie pri kubických rovníc
Odporúčaná literatúra - Polák. J.: Didaktika matematiky
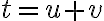
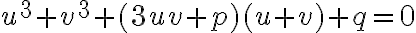
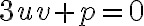
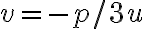
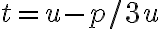
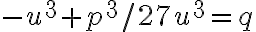
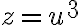

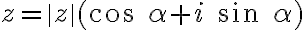
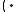
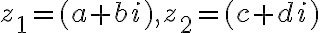
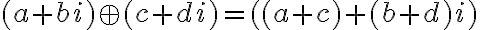
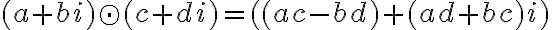
![i= [0,1] i= [0,1]](https://lms.umb.sk/filter/tex/pix.php/e5ef46ed888e0bbcf4abbd53d5bc164b.png)
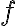
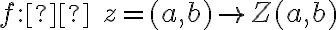
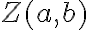
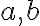
![z= [a, b] z= [a, b]](https://lms.umb.sk/filter/tex/pix.php/69e2dea54d7631e92336a51295e5222e.png)

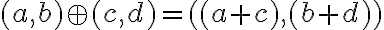

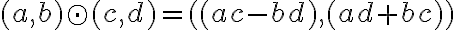
![|z| = \sqrt[]{x^2 + y^2} = \sqrt[]{z \bar{z}} \geq 0 |z| = \sqrt[]{x^2 + y^2} = \sqrt[]{z \bar{z}} \geq 0](https://lms.umb.sk/filter/tex/pix.php/71b1fed67f090f22328bb1f213f5c57f.png)
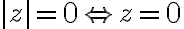
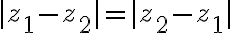
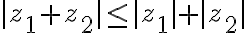
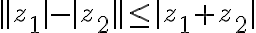
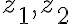
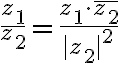
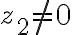
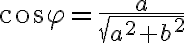
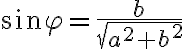

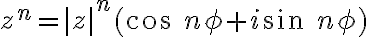

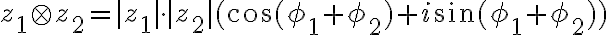
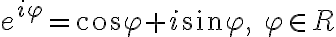
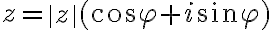
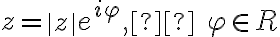
![2+2i,\;\;5i,\;\;-4,\;\;- \sqrt[]{3}+i 2+2i,\;\;5i,\;\;-4,\;\;- \sqrt[]{3}+i](https://lms.umb.sk/filter/tex/pix.php/e5b308432b512f0be438d0b00f449d11.png)