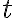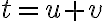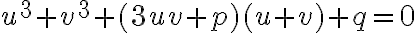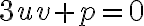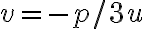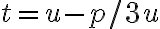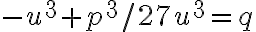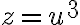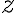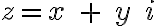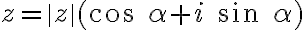Komplexné čísla na strednej škole
Komplexné čísla na strednej škole
Motivačným zdrojom pre zavedenie oboru komplexných čísel je "neriešiteľnosť" rovnice 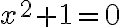 . Žiakom už na ZŠ by sme mali odôvodniť, že
. Žiakom už na ZŠ by sme mali odôvodniť, že
Súčet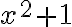 pre ľubovoľné reálne číslo
pre ľubovoľné reálne číslo 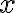 vždy bude kladné číslo
vždy bude kladné číslo
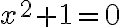 . Žiakom už na ZŠ by sme mali odôvodniť, že
. Žiakom už na ZŠ by sme mali odôvodniť, že
Súčet
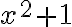 pre ľubovoľné reálne číslo
pre ľubovoľné reálne číslo 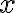 vždy bude kladné číslo
vždy bude kladné číslo
Preto rovnica 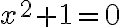 nemá v obore reálnych čísel riešenie
nemá v obore reálnych čísel riešenie
Na SŠ sa často použije formulácia: Číslo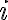 definujeme ako riešenie takejto rovnice. Nech
definujeme ako riešenie takejto rovnice. Nech 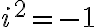 , potom ...
, potom ...
Vhodnejšie by bola formulácia typu: Na chvíľu si predstavme, že také číslo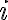 už máme. Nech platí
už máme. Nech platí 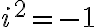 , potom ...
, potom ...
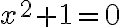 nemá v obore reálnych čísel riešenie
nemá v obore reálnych čísel riešenie
Na SŠ sa často použije formulácia: Číslo
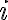 definujeme ako riešenie takejto rovnice. Nech
definujeme ako riešenie takejto rovnice. Nech 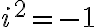 , potom ...
, potom ...
Vhodnejšie by bola formulácia typu: Na chvíľu si predstavme, že také číslo
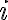 už máme. Nech platí
už máme. Nech platí 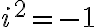 , potom ...
, potom ...
Historický rámec zavedenia pojmu komplexného čísla
- Motivačným zdrojom pre zavedenie oboru komplexných čísel nebol problém riešenia kvadratickej rovnice so záporným diskriminantom.
- Podnetom bol iný problém: algebraické riešenie kubických rovníc.
Kubická rovnica
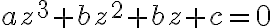 sa po substitúcii
sa po substitúcii
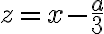 redukuje na tvar
redukuje na tvar
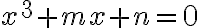 (14.st., Florencia).
(14.st., Florencia).
Potom stačí uvažovať o troch typoch kubických rovníc: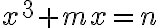 ,
,
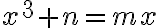 a
a
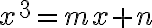 , kde
, kde
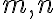 sú kladné koeficienty.
sú kladné koeficienty.
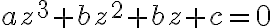 sa po substitúcii
sa po substitúcii
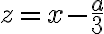 redukuje na tvar
redukuje na tvar
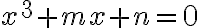 (14.st., Florencia).
(14.st., Florencia).
Potom stačí uvažovať o troch typoch kubických rovníc:
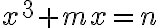 ,
,
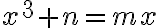 a
a
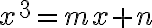 , kde
, kde
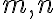 sú kladné koeficienty.
sú kladné koeficienty.
Kubickú rovnicu
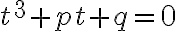 môžeme riešiť
môžeme riešiť
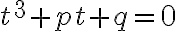 môžeme riešiť
môžeme riešiť
- substitúciou
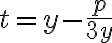 , ktorú použil Thomas Harriot (1560-1621)
, ktorú použil Thomas Harriot (1560-1621) - dostaneme rovnicu šiesteho stupňa, ktorá po úprave vedie k riešeniu
- alebo originál Cardanovou metódou, pozri Wikipédiu. Genialita Cardanovho riešenia spočíta v zavedení