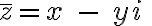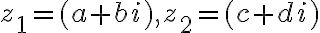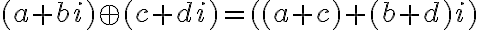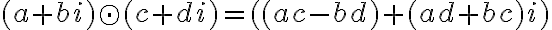Komplexné čísla na strednej škole
Komplexné čísla na strednej škole
Rovnica 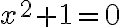 nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor
nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor 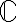 , kde rovnice tohto typu budú mať riešenie.
, kde rovnice tohto typu budú mať riešenie.
Budeme požadovať, aby existovalo nejaké „imaginárne “ číslo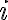 , pre ktoré je druhá mocnina rovná
, pre ktoré je druhá mocnina rovná 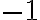 .
.
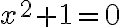 nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor
nemá v obore reálnych čísel riešenie, preto vytvorme taký číselný obor 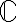 , kde rovnice tohto typu budú mať riešenie.
, kde rovnice tohto typu budú mať riešenie. Budeme požadovať, aby existovalo nejaké „imaginárne “ číslo
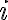 , pre ktoré je druhá mocnina rovná
, pre ktoré je druhá mocnina rovná 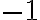 .
.
Predstavme si, že také číslo 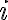 už máme. Nech platí
už máme. Nech platí
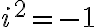 , potom zrejme bude platiť aj rovnosť
, potom zrejme bude platiť aj rovnosť
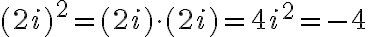 resp. pre ľubovoľné reálne číslo
resp. pre ľubovoľné reálne číslo  bude
bude
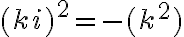 . Čísla
. Čísla
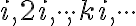 nie sú reálne. Nazveme ich „imaginárne čísla“.
nie sú reálne. Nazveme ich „imaginárne čísla“.
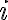 už máme. Nech platí
už máme. Nech platí
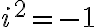 , potom zrejme bude platiť aj rovnosť
, potom zrejme bude platiť aj rovnosť
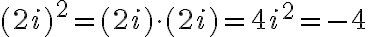 resp. pre ľubovoľné reálne číslo
resp. pre ľubovoľné reálne číslo  bude
bude
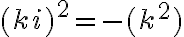 . Čísla
. Čísla
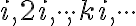 nie sú reálne. Nazveme ich „imaginárne čísla“.
nie sú reálne. Nazveme ich „imaginárne čísla“.
Pri vytváraní číselného oboru 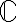 budeme požadovať, aby
budeme požadovať, aby
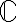 budeme nazývať komplexné čísla a budeme ich zapisovať v tvare
budeme nazývať komplexné čísla a budeme ich zapisovať v tvare 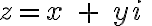 .
.
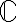 budeme požadovať, aby
budeme požadovať, aby
-
všetky súčty
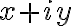 , kde
, kde 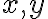 sú ľubovoľné reálne čísla, patrili opäť do oboru
sú ľubovoľné reálne čísla, patrili opäť do oboru 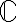
-
dva prvky
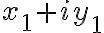 ,
, 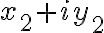 sa rovnali práve vtedy, keď
sa rovnali práve vtedy, keď 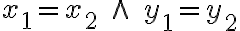
- boli vhodne definované operácie sčítania a násobenia
 budeme nazývať komplexné čísla a budeme ich zapisovať v tvare
budeme nazývať komplexné čísla a budeme ich zapisovať v tvare 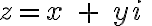 .
.
Reálne číslo
 sa nazýva reálna časť komplexného čísla
sa nazýva reálna časť komplexného čísla
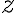 a označujeme ju symbolom
a označujeme ju symbolom
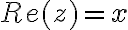
Reálne číslo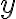 sa nazýva imaginárna časť komplexného čísla
sa nazýva imaginárna časť komplexného čísla
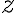 a označujeme ju symbolom
a označujeme ju symbolom
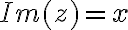
Opačné číslo ku komplexnému číslu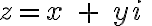 je komplexné číslo
je komplexné číslo
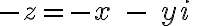
Komplexne združené číslo ku komplexnému číslu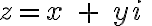 je komplexné číslo
je komplexné číslo 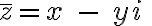
 sa nazýva reálna časť komplexného čísla
sa nazýva reálna časť komplexného čísla
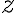 a označujeme ju symbolom
a označujeme ju symbolom
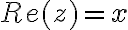
Reálne číslo
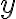 sa nazýva imaginárna časť komplexného čísla
sa nazýva imaginárna časť komplexného čísla
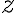 a označujeme ju symbolom
a označujeme ju symbolom
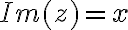
Opačné číslo ku komplexnému číslu
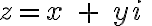 je komplexné číslo
je komplexné číslo
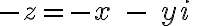
Komplexne združené číslo ku komplexnému číslu
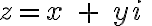 je komplexné číslo
je komplexné číslo