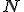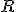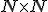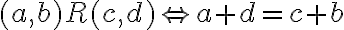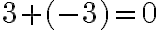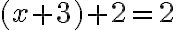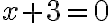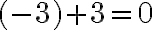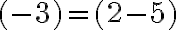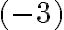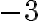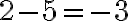Číselné obory na základných a stredných školách
Číselné obory na základných a stredných školách
Celé čísla
Jedna z náročných ale zároveň dôležitých etáp pri rozširovaní číselných oborov na základnej škole je rozšírenie oboru prirodzených čísle na obor celých čísel.
Zavedenie oboru celých čísel je v súčasnosti zakotvené v učebných osnovách pre 8. ročník ZŠ. Východiskovým pojmom je opačné číslo.
Prv než začneme s charakteristikou procesu výstavby celých čísel na ZŠ a komparáciou učebníc matematiky používaných na ZŠ, uvedieme teoretické východiská k tejto problematike.
Motiváciou pri zavádzaní celých čísel môže byť problém, ktorý nastane pri pokuse riešiť niektoré lineárne rovnice v obore prirodzených čísel. Napríklad:
Prv než začneme s charakteristikou procesu výstavby celých čísel na ZŠ a komparáciou učebníc matematiky používaných na ZŠ, uvedieme teoretické východiská k tejto problematike.
Motiváciou pri zavádzaní celých čísel môže byť problém, ktorý nastane pri pokuse riešiť niektoré lineárne rovnice v obore prirodzených čísel. Napríklad:
Jednoduchá algebraická rovnica 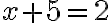 , ktorej koeficienty
, ktorej koeficienty 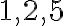 sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
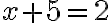 , ktorej koeficienty
, ktorej koeficienty 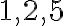 sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
sú prirodzené čísla nemá v obore prirodzených čísel riešenie.
- Ak budeme aplikovať ekvivalentnú úpravu „odčítanie“ čísla
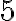 k obidvom stranám rovnice, tak dostaneme
k obidvom stranám rovnice, tak dostaneme 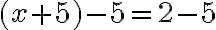 .
. - Po úprave na ľavej strane rovnice dostaneme
 a na pravej strane dostanem riešenie v tvare
a na pravej strane dostanem riešenie v tvare  .
. - Veľmi ľahko sa presvedčíme, že rozdiel
 v obore prirodzených čísle neexistuje. Preto je nutné vytvoriť číselný obor, v ktorom takýto rozdiel existuje.
v obore prirodzených čísle neexistuje. Preto je nutné vytvoriť číselný obor, v ktorom takýto rozdiel existuje. - Myšlienka vytvorenia nového číselného oboru pomocou "rozdielov dvoch prirodzených čísel" je nosnou pri zavádzaní oboru celých čísel v teoretickej aritmetike na VŠ.
Vysoká škola - teoretická aritmetika
Na začiatku je vhodné (aj keď nie nutné) zaviesť pojem opačného čísla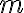 k ľubovoľnému prirodzenému číslu
k ľubovoľnému prirodzenému číslu  , ktoré sa definuje pomocou rovnosti
, ktoré sa definuje pomocou rovnosti
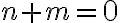 .
.
Celé čísla zavedieme pomocou vhodnej relácie ekvivalencie a rozkladu karteziánskeho súčinu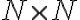 množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
Pozrite si vlastnosti tejto relácie Tu
Na začiatku je vhodné (aj keď nie nutné) zaviesť pojem opačného čísla
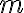 k ľubovoľnému prirodzenému číslu
k ľubovoľnému prirodzenému číslu  , ktoré sa definuje pomocou rovnosti
, ktoré sa definuje pomocou rovnosti
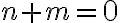 .
.
Celé čísla zavedieme pomocou vhodnej relácie ekvivalencie a rozkladu karteziánskeho súčinu
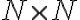 množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
množiny prirodzených čísel
podľa takejto relácie ekvivalencie. Na prednáškach z teoretickej aritmetiky sa dozviete, že táto relácia je definovaná nasledovne:
Nech 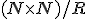 je rozklad karteziánskeho súčinu
je rozklad karteziánskeho súčinu 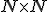 , potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel
, potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel 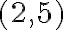 a
a 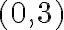 patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo
patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo 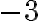 .
.
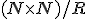 je rozklad karteziánskeho súčinu
je rozklad karteziánskeho súčinu 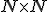 , potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel
, potom triedy tohto rozkladu môžeme považovať za celé čísla, ak zadefinujeme vhodné operácie súčtu a súčinu. Napríklad usporiadané dvojice prirodzených čísel 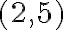 a
a 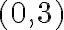 patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo
patria do tej istej triedy rozkladu a teda predstavujú to isté "záporné" číslo 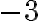 .
.
Vráťme sa teraz do 8. ročníka základnej školy a pokúsme sa vyriešiť rovnicu 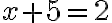 .
.
Pri jej riešení môžeme použiť aj nasledovný postup: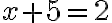 Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi:
Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi: 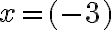 resp.
resp. 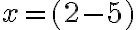 .
.
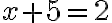 .
.Pri jej riešení môžeme použiť aj nasledovný postup:
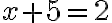 Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi:
Zistili sme, že riešenie môžeme zapísať dvomi spôsobmi: 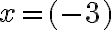 resp.
resp. 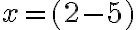 .
.
Závery:
Historické pozadie
Záporné čísla sa objavili po prvýkrát v čínskej matematike. V knihe „Deväť kapitol matematického umenia“ (202 pred n.l.) sú použité červené „úsečky“ pre kladné čísla a čierne pre záporné čísla.
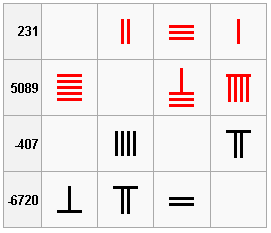
Tento systém je opak súčasného zapisovania kladných a záporných čísel v oblasti bankovníctva, účtovníctva a obchode.
Záporné čísla sa objavili po prvýkrát v čínskej matematike. V knihe „Deväť kapitol matematického umenia“ (202 pred n.l.) sú použité červené „úsečky“ pre kladné čísla a čierne pre záporné čísla.

Tento systém je opak súčasného zapisovania kladných a záporných čísel v oblasti bankovníctva, účtovníctva a obchode.
- V 7. storočí nášho letopočtu v Indii, boli záporné čísla použité na vyjadrenie dlhu. Indický matematik Brahmagupta, uvádza pravidlá pre operácie sčítania a násobenia so zápornými číslami. Používal termíny "dlh“ a „úver“.
- Európski matematici sa bránili konceptu záporných číslach až do 17. storočia, hoci Fibonacci používal pri riešení finančných problémov záporné čísla (Libier Abaci, 1202).
- Gottfried Wilhelm Leibniz bol prvý matematik, ktorý systematicky využíval záporné čísla.
Poznámka
Matematici v rôznych historických obdobiach považovali záporné čísla za absurdné (Diofantos), klamné (Descart) a fiktívne (Bombelli).
Matematici v rôznych historických obdobiach považovali záporné čísla za absurdné (Diofantos), klamné (Descart) a fiktívne (Bombelli).