Didaktika matematiky - východiská
Odborová didaktika
Historické medzníky
Korene didaktiky matematiky a medzníky jej vývoja v 20. storočí
- V roku 1872 Felix Klein publikoval Erlangenský program1) a predniesol prednášku o matematickom vzdelávaní, v ktorej apeloval na väčšiu aplikovateľnosť matematiky pri jej vyučovaní. Ku konci svojej kariéry sa začal zaujímať i o výuku matematiky na nemeckých školách, snažil sa o modernizáciu matematiky. Presadil, aby sa na stredných školách vyučovali základy teorie funkcií a základy diferenciálneho a integrálneho počtu (tzv. Kleinsche Reform). Neskôr aktívne prispel k tomu, aby bola didaktika matematiky uznaná ako vedná disciplína. Viac Tu.
- Dôležitým medzníkom bol rok 1908 a Štvrtý medzinárodný kongres matematikov v Ríme, počas ktorého bola ustanovená nová organizácia:
International Commision on Mathematical Instruction
(Medzinárodný výbor pre výučbu matematiky), ktorej prezidentom sa stal práve Felix Klein. Linka na web Tu. - Ďalším významným krokom bolo vytvorenie
Commission for the Study and Improvement of Mathematics Teaching - CIEAEM
(Komisia pre štúdium a rozvoj vyučovania matematiky) v roku 1950. Linka na web Tu. - Šesťdesiate roky 20. storočia sú obdobím, keď matematici „znovu objavujú“ školu. Objavuje sa hnutie New Math (Nová matematika) u nás známe ako
Modernizácia vyučovania matematiky. - V roku 1970 časopis
Journal for Research in Mathematics Education,
ktorý sa zaradil medzi najrenomovanejšie vedecké časopisy týkajúce sa problematiky didaktiky matematiky.
Poznámky.
- Významný zdroj voľne dostupných publikácií z matematiky na DML-CZ (Czech Digital Mathematics Library), kde sú uvedené takmer všetky ročníky cesko-slovenských časopisov venovaných vyučovaniu matematiky. Linka na web Tu.
- Pozrite si prácu zo šesťdesiatych roky 20. storočia "Programovaná učebnice moderní matematiky", ktorá sumarizuje historické etapy modernizácie vyučovania matematiky v Európe. (str. 34 - 41, zdroj Tu)
Vzťah didaktiky matematiky k dejinám matematiky
Dejiny matematiky približujú spojenie matematiky so životom, odhaľujú proces tvorby
matematických pojmov a tvrdení.
Historické vsuvky na hodinách matematiky žiakov motivujú, odbúravajú strach z matematiky. Priblížením histórie matematiky môžeme získať užitočné predstavy o vývoji matematického myslenia a tieto potom ďalej aplikovať vo vyučovaní.
Podľa P. M. Erdnija:
„Rast stromu matematických znalostí v hlave jedného človeka bude úspešný len vtedy, keď v určitej miere zopakuje históriu rozvoja tejto vedy“2).
Keď sledujeme vývoj vzniku určitého matematického pojmu v histórii ľudstva, a následne pozorujeme myšlienkový proces u našich žiakov, často nachádzame zaujímavú paralelu. Môžeme to pozorovať a porovnávať na vývoji matematického myslenie z obdobia starobylých civilizácií (Egypt, Mezopotámia) s myslením Grékov, Arabov a Európanov v neskoršom období.
Matematické myslenie u Grékov je jasný posun k abstraktnejšiemu mysleniu. Pozrite si Tu.
Podobný proces sa deje aj v školskej matematike: od experimentovania v mladšom veku, žiaci postupne prechádzajú ku kauzálnemu mysleniu v staršom veku. Porovnajte vyučovanie matematiky v starovekom Egypte a v súčasnosti, na príklade riešenia úlohy z Rhindovho papyrusu.
„Rast stromu matematických znalostí v hlave jedného človeka bude úspešný len vtedy, keď v určitej miere zopakuje históriu rozvoja tejto vedy“2).
Keď sledujeme vývoj vzniku určitého matematického pojmu v histórii ľudstva, a následne pozorujeme myšlienkový proces u našich žiakov, často nachádzame zaujímavú paralelu. Môžeme to pozorovať a porovnávať na vývoji matematického myslenie z obdobia starobylých civilizácií (Egypt, Mezopotámia) s myslením Grékov, Arabov a Európanov v neskoršom období.
Matematické myslenie u Grékov je jasný posun k abstraktnejšiemu mysleniu. Pozrite si Tu.
Podobný proces sa deje aj v školskej matematike: od experimentovania v mladšom veku, žiaci postupne prechádzajú ku kauzálnemu mysleniu v staršom veku. Porovnajte vyučovanie matematiky v starovekom Egypte a v súčasnosti, na príklade riešenia úlohy z Rhindovho papyrusu.
Úloha. (Rhindov papyrus - R403))
Je treba rozdeliť 100 chlebov medzi 5 mužov tak, aby bola jedna sedmina z troch horných pre dvoch mužov dole.4)
Je treba rozdeliť 100 chlebov medzi 5 mužov tak, aby bola jedna sedmina z troch horných pre dvoch mužov dole.4)
Poznámky.k pôvodnému riešeniu, ktoré je uvedené na papyruse.
- Celkový počet chlebov je 100 a je potrebné tieto chleby nejakým spôsobom rozdeliť medzi 5 mužov. V úlohe sa spomínajú traja horní muži a dvaja dolní. Toto naznačuje určité usporiadanie, ale nie je celkom isté, že ide o aritmetickú postupnosť. To vyplýva až z prezentovaného riešenia.
- Ďalej je tu podmienka, ktorú je možné interpretovať tak, že súčet počtu chlebov troch horných mužov v usporiadaní sa rovná súčtu chlebov dvoch mužov dole v usporiadaní.
- Upravené pôvodné riešenie prezentujeme v ďalšej podkapitole. Pokúste sa o riešenie prostriedkami školskej matematiky.
- Úloha je riešená metódou chybného predpokladu.
- Táto úloha a jej riešenie poukazujú na ústredné postavenie pojmu zlomok a postupnosti v školskej matematike, s ktorými sa bližšie budeme zoznamovať v tejto lekcii.
Pôvodné riešenie vychádza z predstavy aritmetickej postupnosti tvaru:
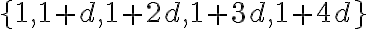 . Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:
. Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:
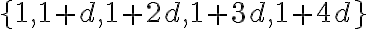 . Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:
. Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:-
Podmienku, že jedna sedmina z troch horných pre dvoch mužov dole, môžeme vyjadriť vzťahom:
![1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)] 1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)]](https://lms.umb.sk/filter/tex/pix.php/721a71393d4ebe6af04bf345f9d3b2ef.png) .
. - Z predchádzajúceho vzťahu vypočítame
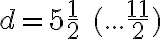 .
. -
Ide teda o postupnosť
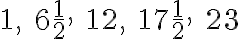 , ktorej súčet je
, ktorej súčet je
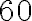 .
. - Číslo
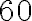 musíme vynásobiť číslom
musíme vynásobiť číslom
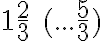 , aby sme získali požadovaný súčet
, aby sme získali požadovaný súčet
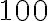 .
. - Týmto číslom musíme preto vynásobiť aj členy vyššie uvedenej postupnosti.
Poznámky.
Tento výsledok však na papyruse nie je uvedený. V súčasnosti by sa táto úloha mohla riešiť takto:
Tento výsledok však na papyruse nie je uvedený. V súčasnosti by sa táto úloha mohla riešiť takto:
________________________________________________________________________________
1) Erlangenský program je v matematice metoda, charakterizující geometrie na základě teorie grup. Dostupné Tu
2) Erndnijev, P. M.:Prepodavanije matematiky v škole. Moskva, Prosvedčenije 1978
3) Rhindov papyrus bol napísaný pisárom Ahmosem asi v 1650 pred naším letopočtom (prepis od Amenehmet III z 19. storočia p.n.l.). Viac Tu.
4) Bečvár J., Bečvářová M., Vymazalová H.(ed.): Matematika ve starověku Egypt a Mezopotámie. Prometheus, Praha 2003, s. 69. Dostupné Tu.
1) Erlangenský program je v matematice metoda, charakterizující geometrie na základě teorie grup. Dostupné Tu
2) Erndnijev, P. M.:Prepodavanije matematiky v škole. Moskva, Prosvedčenije 1978
3) Rhindov papyrus bol napísaný pisárom Ahmosem asi v 1650 pred naším letopočtom (prepis od Amenehmet III z 19. storočia p.n.l.). Viac Tu.
4) Bečvár J., Bečvářová M., Vymazalová H.(ed.): Matematika ve starověku Egypt a Mezopotámie. Prometheus, Praha 2003, s. 69. Dostupné Tu.
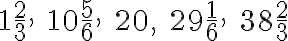
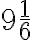
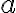
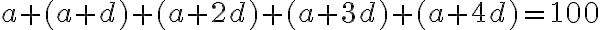
![a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )] a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )]](https://lms.umb.sk/filter/tex/pix.php/219e6357055177f12e194534998ec02b.png)
