Didaktika matematiky - východiská
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Didaktika matematiky - východiská |
| Vytlačil(a): | Guest user |
| Dátum: | streda, 3 júla 2024, 11:37 |
Odborová didaktika
V škole sa má nielen učiť, ale aj naučiť.1
V súčasnosti učiteľ matematiky sa dostáva do pozície koordinátora a manažéra vo vyučovacom procese, ktorý sa snaží o rozvíjanie zásadných
matematických kompetencií žiakov. Funkcia autoritatívneho školiteľa, ktorý vyžaduje len memorovanie matematických definícií a tvrdení sa stáva skôr podpornou.
Výučbu treba chápať ako tvorivý a neopakovateľný proces, ktorý sa nedá spútať do presných schém, modelov, či spojiť len s jedinou teóriou.
Moderná didaktika sa chápe ako disciplína, ktorej predmetom skúmania je proces výučby ako jednota činnosti učiteľa (učenie) a činnosti žiakov (učenie sa). Zaoberá sa procesom výučby vo všeobecnosti, bez ohľadu na konkrétny vyučovací predmet. Komenský: Veľká didaktika →
Moderná didaktika sa chápe ako disciplína, ktorej predmetom skúmania je proces výučby ako jednota činnosti učiteľa (učenie) a činnosti žiakov (učenie sa). Zaoberá sa procesom výučby vo všeobecnosti, bez ohľadu na konkrétny vyučovací predmet. Komenský: Veľká didaktika →
Odborové didaktiky sa zaoberajú skúmaním procesu výučby v určitých skupinách príbuzných vyučovacích predmetov (Turek, 1990, s.10).
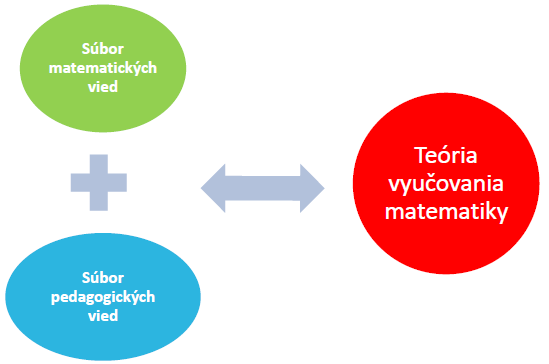
Didaktika matematiky skúma procesy v školskej matematike. Didaktika matematiky analyzuje obsah, prostriedky, metódy a formy vyučovania a štúdia matematiky.
Pre termín Didaktika matematiky sa v niektorých prácach používa termín Teória vyučovania matematiky2). V práci "Matematika jako pedagogický problém"3) sa uvádza aj zaužívaný anglický termín od E. Whittmann "Mathematics Education". Komparáciou viacerých prác a viacerých autorov uvedieme hlavné charakteristiky pre vymedzenie pojmu didaktika matematiky.
Pre termín Didaktika matematiky sa v niektorých prácach používa termín Teória vyučovania matematiky2). V práci "Matematika jako pedagogický problém"3) sa uvádza aj zaužívaný anglický termín od E. Whittmann "Mathematics Education". Komparáciou viacerých prác a viacerých autorov uvedieme hlavné charakteristiky pre vymedzenie pojmu didaktika matematiky.
Didaktika matematiky
- jej cieľom je výskum nových, efektívnejších metód vyučovania matematiky na všetkých stupňoch vzdelávania a ich aplikácie do školskej praxe
- je založená predovšetkým na poznatkoch základných matematických disciplín, na historickom vývoji matematiky ako vedy a ich aplikácií do školskej matematiky
- výsledky experimentov aplikuje do prípravy budúcich učiteľov matematiky, pričom využíva najnovšie výsledky v oblasti pedagogicko-psychologických disciplín a moderné informačno-komunikačné technológie.
Historické medzníky
Korene didaktiky matematiky a medzníky jej vývoja v 20. storočí
- V roku 1872 Felix Klein publikoval Erlangenský program1) a predniesol prednášku o matematickom vzdelávaní, v ktorej apeloval na väčšiu aplikovateľnosť matematiky pri jej vyučovaní. Ku konci svojej kariéry sa začal zaujímať i o výuku matematiky na nemeckých školách, snažil sa o modernizáciu matematiky. Presadil, aby sa na stredných školách vyučovali základy teorie funkcií a základy diferenciálneho a integrálneho počtu (tzv. Kleinsche Reform). Neskôr aktívne prispel k tomu, aby bola didaktika matematiky uznaná ako vedná disciplína. Viac Tu.
- Dôležitým medzníkom bol rok 1908 a Štvrtý medzinárodný kongres matematikov v Ríme, počas ktorého bola ustanovená nová organizácia:
International Commision on Mathematical Instruction
(Medzinárodný výbor pre výučbu matematiky), ktorej prezidentom sa stal práve Felix Klein. Linka na web Tu. - Ďalším významným krokom bolo vytvorenie
Commission for the Study and Improvement of Mathematics Teaching - CIEAEM
(Komisia pre štúdium a rozvoj vyučovania matematiky) v roku 1950. Linka na web Tu. - Šesťdesiate roky 20. storočia sú obdobím, keď matematici „znovu objavujú“ školu. Objavuje sa hnutie New Math (Nová matematika) u nás známe ako
Modernizácia vyučovania matematiky. - V roku 1970 časopis
Journal for Research in Mathematics Education,
ktorý sa zaradil medzi najrenomovanejšie vedecké časopisy týkajúce sa problematiky didaktiky matematiky.
Poznámky.
- Významný zdroj voľne dostupných publikácií z matematiky na DML-CZ (Czech Digital Mathematics Library), kde sú uvedené takmer všetky ročníky cesko-slovenských časopisov venovaných vyučovaniu matematiky. Linka na web Tu.
- Pozrite si prácu zo šesťdesiatych roky 20. storočia "Programovaná učebnice moderní matematiky", ktorá sumarizuje historické etapy modernizácie vyučovania matematiky v Európe. (str. 34 - 41, zdroj Tu)
Vzťah didaktiky matematiky k dejinám matematiky
Dejiny matematiky približujú spojenie matematiky so životom, odhaľujú proces tvorby
matematických pojmov a tvrdení.
Historické vsuvky na hodinách matematiky žiakov motivujú, odbúravajú strach z matematiky. Priblížením histórie matematiky môžeme získať užitočné predstavy o vývoji matematického myslenia a tieto potom ďalej aplikovať vo vyučovaní.
Podľa P. M. Erdnija:
„Rast stromu matematických znalostí v hlave jedného človeka bude úspešný len vtedy, keď v určitej miere zopakuje históriu rozvoja tejto vedy“2).
Keď sledujeme vývoj vzniku určitého matematického pojmu v histórii ľudstva, a následne pozorujeme myšlienkový proces u našich žiakov, často nachádzame zaujímavú paralelu. Môžeme to pozorovať a porovnávať na vývoji matematického myslenie z obdobia starobylých civilizácií (Egypt, Mezopotámia) s myslením Grékov, Arabov a Európanov v neskoršom období.
Matematické myslenie u Grékov je jasný posun k abstraktnejšiemu mysleniu. Pozrite si Tu.
Podobný proces sa deje aj v školskej matematike: od experimentovania v mladšom veku, žiaci postupne prechádzajú ku kauzálnemu mysleniu v staršom veku. Porovnajte vyučovanie matematiky v starovekom Egypte a v súčasnosti, na príklade riešenia úlohy z Rhindovho papyrusu.
„Rast stromu matematických znalostí v hlave jedného človeka bude úspešný len vtedy, keď v určitej miere zopakuje históriu rozvoja tejto vedy“2).
Keď sledujeme vývoj vzniku určitého matematického pojmu v histórii ľudstva, a následne pozorujeme myšlienkový proces u našich žiakov, často nachádzame zaujímavú paralelu. Môžeme to pozorovať a porovnávať na vývoji matematického myslenie z obdobia starobylých civilizácií (Egypt, Mezopotámia) s myslením Grékov, Arabov a Európanov v neskoršom období.
Matematické myslenie u Grékov je jasný posun k abstraktnejšiemu mysleniu. Pozrite si Tu.
Podobný proces sa deje aj v školskej matematike: od experimentovania v mladšom veku, žiaci postupne prechádzajú ku kauzálnemu mysleniu v staršom veku. Porovnajte vyučovanie matematiky v starovekom Egypte a v súčasnosti, na príklade riešenia úlohy z Rhindovho papyrusu.
Úloha. (Rhindov papyrus - R403))
Je treba rozdeliť 100 chlebov medzi 5 mužov tak, aby bola jedna sedmina z troch horných pre dvoch mužov dole.4)
Je treba rozdeliť 100 chlebov medzi 5 mužov tak, aby bola jedna sedmina z troch horných pre dvoch mužov dole.4)
Poznámky.k pôvodnému riešeniu, ktoré je uvedené na papyruse.
- Celkový počet chlebov je 100 a je potrebné tieto chleby nejakým spôsobom rozdeliť medzi 5 mužov. V úlohe sa spomínajú traja horní muži a dvaja dolní. Toto naznačuje určité usporiadanie, ale nie je celkom isté, že ide o aritmetickú postupnosť. To vyplýva až z prezentovaného riešenia.
- Ďalej je tu podmienka, ktorú je možné interpretovať tak, že súčet počtu chlebov troch horných mužov v usporiadaní sa rovná súčtu chlebov dvoch mužov dole v usporiadaní.
- Upravené pôvodné riešenie prezentujeme v ďalšej podkapitole. Pokúste sa o riešenie prostriedkami školskej matematiky.
- Úloha je riešená metódou chybného predpokladu.
- Táto úloha a jej riešenie poukazujú na ústredné postavenie pojmu zlomok a postupnosti v školskej matematike, s ktorými sa bližšie budeme zoznamovať v tejto lekcii.
Pôvodné riešenie vychádza z predstavy aritmetickej postupnosti tvaru:
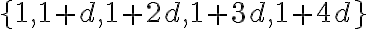 . Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:
. Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:
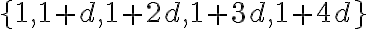 . Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:
. Chybným predpokladom je to, že prvým členom tejto postupnosti explicitne stanovili číslo 1. Stručný prepis riešenia tejto úlohy zaznamenaného na papyruse:-
Podmienku, že jedna sedmina z troch horných pre dvoch mužov dole, môžeme vyjadriť vzťahom:
![1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)] 1+ (1+d) = 1/7[(1+2d)+(1+3d)+(1+4d)]](https://lms.umb.sk/filter/tex/pix.php/721a71393d4ebe6af04bf345f9d3b2ef.png) .
. - Z predchádzajúceho vzťahu vypočítame
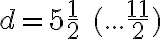 .
. -
Ide teda o postupnosť
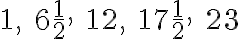 , ktorej súčet je
, ktorej súčet je
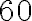 .
. - Číslo
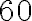 musíme vynásobiť číslom
musíme vynásobiť číslom
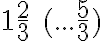 , aby sme získali požadovaný súčet
, aby sme získali požadovaný súčet
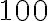 .
. - Týmto číslom musíme preto vynásobiť aj členy vyššie uvedenej postupnosti.
Poznámky.
Tento výsledok však na papyruse nie je uvedený. V súčasnosti by sa táto úloha mohla riešiť takto:
Tento výsledok však na papyruse nie je uvedený. V súčasnosti by sa táto úloha mohla riešiť takto:
________________________________________________________________________________
1) Erlangenský program je v matematice metoda, charakterizující geometrie na základě teorie grup. Dostupné Tu
2) Erndnijev, P. M.:Prepodavanije matematiky v škole. Moskva, Prosvedčenije 1978
3) Rhindov papyrus bol napísaný pisárom Ahmosem asi v 1650 pred naším letopočtom (prepis od Amenehmet III z 19. storočia p.n.l.). Viac Tu.
4) Bečvár J., Bečvářová M., Vymazalová H.(ed.): Matematika ve starověku Egypt a Mezopotámie. Prometheus, Praha 2003, s. 69. Dostupné Tu.
1) Erlangenský program je v matematice metoda, charakterizující geometrie na základě teorie grup. Dostupné Tu
2) Erndnijev, P. M.:Prepodavanije matematiky v škole. Moskva, Prosvedčenije 1978
3) Rhindov papyrus bol napísaný pisárom Ahmosem asi v 1650 pred naším letopočtom (prepis od Amenehmet III z 19. storočia p.n.l.). Viac Tu.
4) Bečvár J., Bečvářová M., Vymazalová H.(ed.): Matematika ve starověku Egypt a Mezopotámie. Prometheus, Praha 2003, s. 69. Dostupné Tu.
Poznávací proces
Mark Twain:
"Vysoká škola je miestom, kde poznámky z prednášok profesorov idú rovno do študentovho zápisníka bez toho, aby prešli mozgom."
Profesor Hejný:
"Matematické poznání člověka má dvě rozsáhle oblasti, které pokrývají většinu tohoto teritoria lidského intelektu: obsah a schopnosti."1)
"Matematické poznání člověka má dvě rozsáhle oblasti, které pokrývají většinu tohoto teritoria lidského intelektu: obsah a schopnosti."1)
Naša znalosť obsahu matematického poznania (znalostí) je dosť bohatá, ale naša znalosť súboru matematických schopností zatiaľ zaostáva za obsahom.
Problémom je aj skutočnosť, že schopnosti (napr. experimentovanie, analyzovanie situácie, objavovanie, argumentácia, ...) presahujú oblasť matematiky. Z toho plynie, že rozvoj schopností je dôležitejšia než rozvoj znalostí.
Problémom je aj skutočnosť, že schopnosti (napr. experimentovanie, analyzovanie situácie, objavovanie, argumentácia, ...) presahujú oblasť matematiky. Z toho plynie, že rozvoj schopností je dôležitejšia než rozvoj znalostí.
Osvojovanie matematických schopností je úzko spojené s duševným výkonom žiaka, ktorého dôležitou súčasťou je proces abstrakcie.
Poznávací proces bol skúmaný mnohými bádateľmi. Pokúsime sa v krátkosti charakterizovať konštruktivistický prístup profesora Hejného. Vychádza z toho, že vo vzdelávacom procese žiak/študent
- najskôr vníma a pochopí elementárne javy a súvislosti na viacerých konkrétnych situáciách (separované modely)
- neskôr hľadá čo majú spoločné tieto elementárne javy (generické modely) a následne objavuje obecnejšie javy a vzťahy, pričom prichádza k abstraktnému poznaniu
Motivácia - príbeh o slávnom matematikovi K. F. Gaussovi.
"Ide o pomerne známy príbeh, v ktorom sa hovorí, že keď Gauss navštevoval národnú školu, žiaci jeho triedy dostali za úlohu vypočítať súčet:
1 + 2 + 3 + .......+ 100 = ?
Učiteľ sa domnieval, že si urobí krátku pauzu. Toto mu však zmaril žiak Gauss, ktorý sa vzápätí prihlásil so správnym výsledkom 5050."
"Ide o pomerne známy príbeh, v ktorom sa hovorí, že keď Gauss navštevoval národnú školu, žiaci jeho triedy dostali za úlohu vypočítať súčet:
1 + 2 + 3 + .......+ 100 = ?
Učiteľ sa domnieval, že si urobí krátku pauzu. Toto mu však zmaril žiak Gauss, ktorý sa vzápätí prihlásil so správnym výsledkom 5050."
Pokúste sa urobiť analýzu poznávacieho procesu tejto situácie. Pozrite si text, ktorý analyzuje Gaussovo riešenie Tu.
Matematická obec nie je jednotná v názore na postavenie didaktiky matematiky. Niektorí autori preferujú dôležitosť odborného matematického vzdelania. Podľa ich názoru "byť dobrým učiteľom matematiky" znamená perfektnú odbornú úroveň matematiky.
Na opačnom konci sa nachádza extrémny názor, že dobrým učiteľom matematiky môže byť človek s minimálnymi znalosťami matematiky (približne na úrovni strednej školy).
Podľa profesora Hejného: Dobrý učiteľ matematiky hľadá harmonickú rovnováhu medzi matematikou a vyučovaním.
Veľmi výstižne o "mizernom" učiteľovi matematiky sa vyjadril Karel Čapek takto:
Na opačnom konci sa nachádza extrémny názor, že dobrým učiteľom matematiky môže byť človek s minimálnymi znalosťami matematiky (približne na úrovni strednej školy).
Podľa profesora Hejného: Dobrý učiteľ matematiky hľadá harmonickú rovnováhu medzi matematikou a vyučovaním.
Tvrdenie. (Karel Čapek)
Najmizernejšími učiteľmi matematiky sú "odborní hnidopiši zarajtovaní do uzoučkého okruhu vědátorství" a na druhom póle sú to "školskí řemeselníci, kterí taktak ovládají svou látku ... jejich vyučovaní záleží v tom, že tabule musí být čiste umyta, žáci tiši jako kameny a jednou za čas musejí dostat pumu, kuli ..."
Najmizernejšími učiteľmi matematiky sú "odborní hnidopiši zarajtovaní do uzoučkého okruhu vědátorství" a na druhom póle sú to "školskí řemeselníci, kterí taktak ovládají svou látku ... jejich vyučovaní záleží v tom, že tabule musí být čiste umyta, žáci tiši jako kameny a jednou za čas musejí dostat pumu, kuli ..."
Ukážka deformácie poznávacieho procesu.
- Najčastejšou deformáciou poznávacieho procesu je nedostatočná motivácia. Pri jej zanedbávaní žiaci sa nesnažia preberanú látku pochopiť ale snažia sa hlavne vyhovieť učiteľovi. Často sa potom na hodinách matematiky stretávame s učením spamäti, odpisovaniu, výhovorkách a pod.
- Druhým vážnym nedostatkom poznávacieho procesu je formalizmus v poznávacom procese. V práci Rendl, M., Vondrová, N. a kol. 2013) sa uvádza názor učiteľky z praxe:
"Jedna polovina, krát jedna polovina a ona z toho vyleze jedna štvrtina. Takže jak to ukázat?"
Profesor Kuřina k tomu dodáva, že dotyčná pani učiteľka má medzery v didaktickom vzdelaní resp. pri preberaní zlomkov sa zamerala len na formálnosť (predpis) násobenia zlomkov (súčin čitateľov lomene súčin menovateľov). Zároveň pripomína možnosť interpretovať násobenie reálnych čísel pomocou veľkostí úsečiek, pri ktorej sa súčin interpretuje ako obsah obdĺžnika.
Grafický súčin zlomkov
Cvičenie
Vytvorte applet v GeoGebre pre súčin zlomkov, v ktorom je možné meniť vstupné zlomky pomocou posuvníkov. Pozrite si návrh od Colm Duffin a preklad do SK.
Vytvorte applet v GeoGebre pre súčin zlomkov, v ktorom je možné meniť vstupné zlomky pomocou posuvníkov. Pozrite si návrh od Colm Duffin a preklad do SK.
__________________________________________________________________________
1) Hejný, M. a kol,: Dvacet pět kapitol z didaktiky matematiky.Praha 2004.ISBN 80-7290-189-3 (1. sv.). Dostupné Tu.
2) Rendl, M., Vondrová, N. a kol.: Kritická místa atematiky na základní škole očima učitelu. UK Praha 2013.
1) Hejný, M. a kol,: Dvacet pět kapitol z didaktiky matematiky.Praha 2004.ISBN 80-7290-189-3 (1. sv.). Dostupné Tu.
2) Rendl, M., Vondrová, N. a kol.: Kritická místa atematiky na základní škole očima učitelu. UK Praha 2013.
Poučenie z histórie
V súčasnosti sa pri zavádzaní zlomkov na základnej škole stále stretávame s problémami. Žiaci majú pravidlá práce so zlomkami uchované v pamäti, ale nedokážu:
- použiť jazyk zlomkov pri modelovaní reálnych situácií,
- argumentačne zdôvodniť pravidlá práce so zlomkami.
V predchádzajúcej časti sme poukázali na pomerne dobré zručnosti pri počítaní so zlomkami v starovekom Egypte. Uvedieme ešte jednu ukážku z histórie, ktorá môže slúžiť aj ako motivácia pri experimentovaní so zlomkami na ZŠ. Nasledujúcu úlohu z egyptského papyrusu sa pokúste experimentálne spracovať na rozdeľovanie ( chlebov pre
chlebov pre  ľudí) pomocou separovaného modelu - štvorčekovaného papiera.
ľudí) pomocou separovaného modelu - štvorčekovaného papiera.
 chlebov pre
chlebov pre  ľudí) pomocou separovaného modelu - štvorčekovaného papiera.
ľudí) pomocou separovaného modelu - štvorčekovaného papiera.Úloha z egyptských papyrusov
Spravodlivo rozdeľ 5 chlebov medzi 21 mužov.
Egyptský pisár uviedol, že každý človek by dostal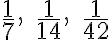 chleba. Ako na to prišiel?
chleba. Ako na to prišiel?
Vytvorte modelovú situáciu, v ktorej významnú úlohu zohrá separovaný model - kmeňové zlomky. Pozrite si študentskú prezentáciu o zlomkoch Tu.
Spravodlivo rozdeľ 5 chlebov medzi 21 mužov.
Egyptský pisár uviedol, že každý človek by dostal
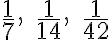 chleba. Ako na to prišiel?
chleba. Ako na to prišiel?
Riešenie úlohy o delení chlebov
Dnešný žiak by úlohu vyriešil tak, že každému mužovi by dal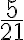 chleba. Také zlomky však v Egypte nepoužívali, egyptskí pisári pracovali len s kmeňovými zlomkami
chleba. Také zlomky však v Egypte nepoužívali, egyptskí pisári pracovali len s kmeňovými zlomkami 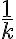 alebo so zlomkami typu
alebo so zlomkami typu 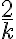 , pre ktoré mali tabuľky rozkladov1). Najskôr urobili rozklad čitateľa
, pre ktoré mali tabuľky rozkladov1). Najskôr urobili rozklad čitateľa 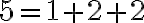 .
.
Dnešný žiak by úlohu vyriešil tak, že každému mužovi by dal
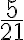 chleba. Také zlomky však v Egypte nepoužívali, egyptskí pisári pracovali len s kmeňovými zlomkami
chleba. Také zlomky však v Egypte nepoužívali, egyptskí pisári pracovali len s kmeňovými zlomkami 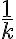 alebo so zlomkami typu
alebo so zlomkami typu 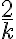 , pre ktoré mali tabuľky rozkladov1). Najskôr urobili rozklad čitateľa
, pre ktoré mali tabuľky rozkladov1). Najskôr urobili rozklad čitateľa 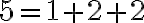 .
. - V tabuľkách vyhľadali, ako je možné 2 chleby rozdeliť medzi 21 ľudí.
- Našli vzťah
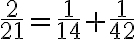 .
. - Podľa takéhoto delenia by každý muž dostal
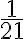 z prvého chleba a
z prvého chleba a 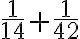 z prvej dvojice chlebov a to isté z druhej dvojice chlebov.
z prvej dvojice chlebov a to isté z druhej dvojice chlebov. - Čo v súčte znamená
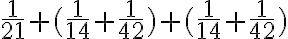 .
. - Po úprave za pomoci spomínaných tabuliek
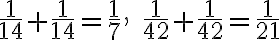 dostali výsledok
dostali výsledok 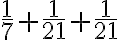 .
. - Opäť za pomoci tabuliek upravili na tvar
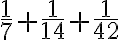 .
.
___________________________________________________________________________
1) Pozri prácu: Bečvár, J.: Matematika ve starém Egyptě, str 55-56. Dostupné Tu.
1) Pozri prácu: Bečvár, J.: Matematika ve starém Egyptě, str 55-56. Dostupné Tu.
Zlomky na ZŠ
Obsahové a výkonové štandardy pre tematický okruh Zlomky na ZŠ zahŕňajú:
- Zlomok ako časť celku, chápať, prečítať, zapísať, znázorniť diagramom
- Zlomok ako číslo, umiestniť na osi. Nulový a jednotkový, pravý a nepravý zlomok. Prevod na zmiešané číslo. Vyjadrenie desatinným číslom.
- Porovnávanie a usporiadanie. Rovnaké zlomky v inom tvare. Základný tvar. Rozširovanie a krátenie.
- Sčítanie a odčítanie zlomkov s rovnakým a rôznym menovateľom.
- Násobenie a delenie zlomkov prirodzeným číslom a zlomkom. Krátenie do kríža. Úprava výsledku na základný tvar, resp. zmiešané číslo.
Na zlomok sa môžeme pozerať z hľadiska mnohosti, operátora a adresy. (Hejný a kol., 1989)
- Mnohosť odpovedá na otázku „Koľko?“
- Operátor sa chápe ako príkaz zmeny, napr. zober z toho 3/4.
- Adresa hovorí o usporiadaní, o zaradení do štruktúry, v matematike ide najčastejšie o umiestnenie na číselnú os.
Applet je dostupný Tu, stiahnite si ho a preložte do slovenčiny!
Profesor Hejný identifikuje kritické miesta vo vyučovaní zlomkov.
- Prvá predstava zlomku je vo forme operátora – nie 3/4 ako číslo, ale ako vziať 3/4 z niečoho. Ako časť koláča, ktorú si odkrojím.
- Pochopiť zlomok ako mnohosť vyžaduje abstrakciu. Pomôžeme si číselnou osou. Zlomok 3/4 predstavuje primárne adresu na číselnej osi. Avšak reprezentuje aj mnohosť – dĺžka úsečky od začiatku osi v čísle 0 po číslo 3/4. A tiež reprezentuje operátor – vyčlenenie troch štvrtín z úsečky s krajnými bodmi 0, 1.
- Pred zavedením súčtu a súčinu zlomkov je potrebné doviesť žiaka od predstavy zlomku ako operátora ku zlomku ako mnohosti.
Pri interpretácii zlomkov využívame tri praktické (klasické) modely :
Ďalší krok je vziať 3/4 z dvoch tort, potom 3/4 z ľubovoľného celočíselného počtu tort a napokon 3/4 z torty, ktorá už raz bola rozkrájaná. Napríklad 3/4 z polovice torty. Názorná dynamická vizualizácia týchto krokov je práve hlavným cieľom DGS.
- úsečka (tyč, doska)
- kruh (torta, pizza)
- obdĺžnik rozdelený na štvorčeky (čokoláda).
Ďalší krok je vziať 3/4 z dvoch tort, potom 3/4 z ľubovoľného celočíselného počtu tort a napokon 3/4 z torty, ktorá už raz bola rozkrájaná. Napríklad 3/4 z polovice torty. Názorná dynamická vizualizácia týchto krokov je práve hlavným cieľom DGS.
Z pohľadu vyššej matematiky (Teoretická aritmetika) zlomky v školskej matematike chápeme ako racionálne čísla, pričom dva zlomky
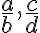 budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
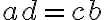
Počas štúdia na VŠ sme zistili, že množina racionálnych čísel obsahuje všetky zlomky, ktorých čitateľ je celé číslo a menovateľ je kladné prirodzené číslo.
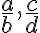 budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
budú predstavovať to isté racionálne číslo, ak bude platiť rovnosť
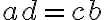
Počas štúdia na VŠ sme zistili, že množina racionálnych čísel obsahuje všetky zlomky, ktorých čitateľ je celé číslo a menovateľ je kladné prirodzené číslo.
Pri zavádzaní operácií sčítania a násobenia racionálnych čísel v školskej matematike sa opierame o sčítanie a násobenie zlomkov. Pre ľubovoľné dva zlomky 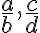 platí:
platí:
sčítanie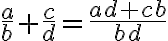
násobenie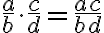
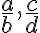 platí:
platí:
sčítanie
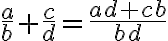
násobenie
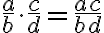
Úloha
Posúďte Cilkino uvažovanie resp. jej riešenie.
Posúďte Cilkino uvažovanie resp. jej riešenie.
Ukážka z práce "Hejný, M. a kol., 25 kapitol z didaktiky matematiky".
Cilka chodí do 6. triedy a doteraz mala samé jednotky. V druhom polroku došlo k zmene učiteľa matematiky, ktorý ku koncu prvej hodiny dal náročnú úlohu.
Úloh
Koľko šestín je nutné pridať k dvom tretinám, aby sme dostali štyri štvrtiny?
Cilkino riešenie
Cilka chcela od pána učiteľa vysvetliť návod na riešenie takýchto úloh. Keď sa dozvedela, že návod neexistuje, zneistela. Za pomoci pána učiteľa a množstva obrázkov, ktoré jej pán učiteľ ponúkol, Cilka nedokázala určiť správny výsledok.
Nevzdávala sa. Nakoniec však zažiarila a zvolala: "Už to viem! Je to na odčítanie zlomkov. Akože 4/4 mínus 2/3. To som vyrátala a dostala som 4/12. Ale to (zvýši hlas) treba ešte vykrátiť dvomi, aby sme mali šestiny. To sú dve šestiny. Takže sú to dva. Je to tak?
Záver - zhodnotenie učiteľa: "Radosť Cilky a moja bezmocnosť spôsobili, že som túto polopravdu zbabelo odsúhlasil a vzdal som sa ďalšieho vysvetľovania."
Úloh
Koľko šestín je nutné pridať k dvom tretinám, aby sme dostali štyri štvrtiny?
Cilkino riešenie
Cilka chcela od pána učiteľa vysvetliť návod na riešenie takýchto úloh. Keď sa dozvedela, že návod neexistuje, zneistela. Za pomoci pána učiteľa a množstva obrázkov, ktoré jej pán učiteľ ponúkol, Cilka nedokázala určiť správny výsledok.
Nevzdávala sa. Nakoniec však zažiarila a zvolala: "Už to viem! Je to na odčítanie zlomkov. Akože 4/4 mínus 2/3. To som vyrátala a dostala som 4/12. Ale to (zvýši hlas) treba ešte vykrátiť dvomi, aby sme mali šestiny. To sú dve šestiny. Takže sú to dva. Je to tak?
Záver - zhodnotenie učiteľa: "Radosť Cilky a moja bezmocnosť spôsobili, že som túto polopravdu zbabelo odsúhlasil a vzdal som sa ďalšieho vysvetľovania."
Poznámky.
- Podľa prof. Hejného: "Zrejme pre Cilku zlomok nie je objekt, ale len dvojica čísel oddelená vodorovnou čiarou." Súhlasíte s týmto názorom?
- V čom je výnimočný Cilkin algebraický postup?
- Pokúste sa vytvoriť vhodný separovaný model, ktorý by pomohol Cilke vyriešiť túto úlohu a argumentačne zdôvodniť riešenie. Náš návrh modelu si stiahnite Tu.
- Analyzujte situáciu keby sme pozmenili úlohu takto: Koľko tretín je nutné pridať k dvom pätinám, aby sme dostali štyri štvrtiny?
- Ktorú z metód v takto pozmenenej úlohe je výhodnejšie aplikovať - Cilkinu, či (nezverejnenú) metódu "nového" učiteľa?
- Nájdite univerzálny (generický) model na interpretáciu úloh typu: Koľko
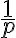 treba pridať k
treba pridať k 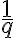 , aby sme dostali
, aby sme dostali 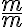 ?
?
Pozrite si knihu appletov ku zlomkom Tu
a prácu Zlomky a Geogebra1)
Seminárne zadania
Domáca úloha.
Vytvorenie appletu - návrh od Colm Duffin - preklad do SK.
Pri riešení nasledujúcich úloh aplikujte konštruktivistický prístup podľa profesora Hejného, v ktorom žiak
- najskôr vníma a pochopí elementárne javy a súvislosti na viacerých konkrétnych situáciách (separované modely),
- neskôr hľadá čo majú spoločné tieto elementárne javy (generické modely),
- a následne objavuje obecnejšie vzťahy, pričom prichádza k abstraktnému poznaniu.
Seminárne cvičenie.
- Analyzujte modifikovanú Celkinu úlohu o zlomkoch: "Koľko tretín je nutné pridať k dvom pätinám, aby sme dostali štyri štvrtiny?"
V GeoGebre vytvorte univerzálny (generický) model na interpretáciu úloh typu: Koľko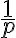 treba pridať k
treba pridať k 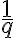 , aby sme dostali
, aby sme dostali 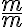 ?
?
Separovaný model pre pôvodnú Celkinu úlohu. - (Domáca úloha) Navrhnite demonštračný applet na prezentáciu podielu dvoch prirodzených čísel pomocou egyptského rozpoľovania a tvorenia iných kmeňových zlomkov1),
ktorá bude vhodná pre žiakov základnej školy.
Inšpirujte sa úlohami z Rhindovho papyrusu zo starovekého Egypta. Prezrite si kurz2). Ukážka egyptského násobenia: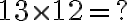 :
:
- (Domáca úloha) Premyslite spôsob ako priblížiť žiakom tvrdenie: Súčin dvoch záporných čísel je kladné reálne číslo. Poznáte nejaké separované modely pre operácie s reálnymi číslami? Aký model by ste pri zdôvodňovaní tvrdenia o súčine dvoch záporných čísel použili?
- (Domáca úloha) Vymyslite príbeh alebo problém, ktorý by viedol k riešeniu
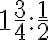 .
.
Pokúste sa najskôr transformovať podiel na súčin a k nemu hľadať vhodnú interpretáciu.
Úloha
Vytvorte alebo nájdite vhodný applet, ktorý vám pomôže zodpovedať otázky:
Ako sa mení hodnota zlomku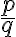 , keď zväčšujeme číslo
, keď zväčšujeme číslo  ?
?
Ako ovplyvňuje hodnotu zlomku zväčšenie menovateľa ?
?
Vytvorte alebo nájdite vhodný applet, ktorý vám pomôže zodpovedať otázky:
Ako sa mení hodnota zlomku
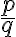 , keď zväčšujeme číslo
, keď zväčšujeme číslo  ?
?
Ako ovplyvňuje hodnotu zlomku zväčšenie menovateľa
 ?
?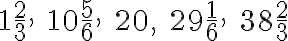
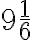
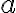
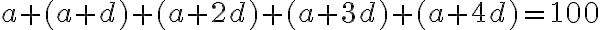
![a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )] a + ( a + d ) = 1/7 [( a + 2d ) + ( a + 3d ) + ( a + 4d )]](https://lms.umb.sk/filter/tex/pix.php/219e6357055177f12e194534998ec02b.png)
