Kubovčík, M.: Kužeľosečky
7. Riadiaca priamka kužeľosečky
7.2. Dôkaz vety pre singulárne kužeľosečky
Nech súradnicová os 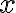 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza pevným bodom
a prechádza pevným bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X [x; y] X [x; y]](https://lms.umb.sk/filter/tex/pix.php/77046f7175b62e08861002c3fc77c3a3.png) platí, že neležia na riadiacej priamke
platí, že neležia na riadiacej priamke  , preto
, preto 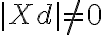 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
:
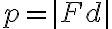 .
.
Súradnice pevne zvoleného bodu sú![F[e;0] F[e;0]](https://lms.umb.sk/filter/tex/pix.php/d45ce59d231cd820e6eddd0c9b0e2176.png) , pričom
, pričom 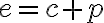 a koeficient
a koeficient 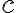 je z rovnice popisujúcu riadiacu priamku
je z rovnice popisujúcu riadiacu priamku 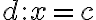 . Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny
. Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny 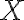 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  platí:
platí:
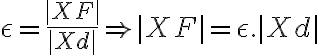
Podrobnejšie si rozoberieme dané vzdialenosti:
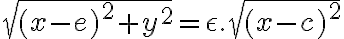
Vytvoríme kvadratickú rovnicu s neznámymi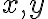 , keďže kužeľosečky sú algebrické krivky 2. stupňa:
, keďže kužeľosečky sú algebrické krivky 2. stupňa:
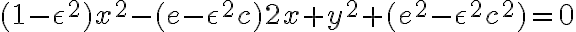
Keďže pevný bod leží na riadiacej priamke
leží na riadiacej priamke  , tak platí
, tak platí 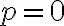 . Riadiaca priamka
. Riadiaca priamka  je vzdialená od počiatku KSS o konštantu
je vzdialená od počiatku KSS o konštantu 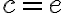 . Vytvorená kvadratická rovnica s neznámymi
. Vytvorená kvadratická rovnica s neznámymi 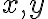 nadobudne nasledujúci tvar:
nadobudne nasledujúci tvar:
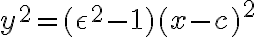
Pomocou poslednej odvodenej rovnice sa budeme zaoberať prípadmi s veľkosťami numerickej excentricity:
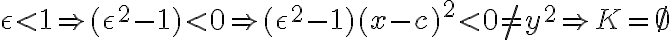 - dostali sme prázdnu množinu
- dostali sme prázdnu množinu
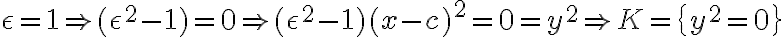 - dostali sme totožné rovnobežky
- dostali sme totožné rovnobežky
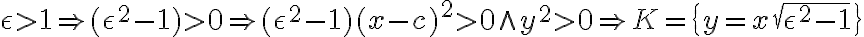 - dostali sme zjednotenie rôznobežiek.
- dostali sme zjednotenie rôznobežiek.
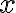 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza pevným bodom
a prechádza pevným bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X [x; y] X [x; y]](https://lms.umb.sk/filter/tex/pix.php/77046f7175b62e08861002c3fc77c3a3.png) platí, že neležia na riadiacej priamke
platí, že neležia na riadiacej priamke  , preto
, preto 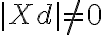 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
: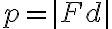 .
.Súradnice pevne zvoleného bodu sú
![F[e;0] F[e;0]](https://lms.umb.sk/filter/tex/pix.php/d45ce59d231cd820e6eddd0c9b0e2176.png) , pričom
, pričom 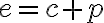 a koeficient
a koeficient 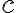 je z rovnice popisujúcu riadiacu priamku
je z rovnice popisujúcu riadiacu priamku 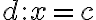 . Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny
. Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny 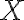 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  platí:
platí: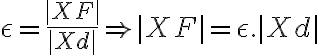
Podrobnejšie si rozoberieme dané vzdialenosti:
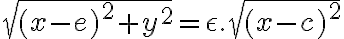
Vytvoríme kvadratickú rovnicu s neznámymi
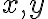 , keďže kužeľosečky sú algebrické krivky 2. stupňa:
, keďže kužeľosečky sú algebrické krivky 2. stupňa: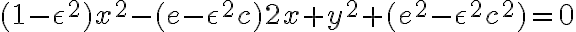
Keďže pevný bod
 leží na riadiacej priamke
leží na riadiacej priamke  , tak platí
, tak platí 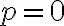 . Riadiaca priamka
. Riadiaca priamka  je vzdialená od počiatku KSS o konštantu
je vzdialená od počiatku KSS o konštantu 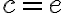 . Vytvorená kvadratická rovnica s neznámymi
. Vytvorená kvadratická rovnica s neznámymi 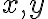 nadobudne nasledujúci tvar:
nadobudne nasledujúci tvar: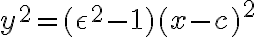
Pomocou poslednej odvodenej rovnice sa budeme zaoberať prípadmi s veľkosťami numerickej excentricity:
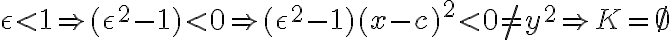 - dostali sme prázdnu množinu
- dostali sme prázdnu množinu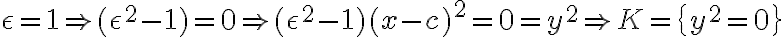 - dostali sme totožné rovnobežky
- dostali sme totožné rovnobežky 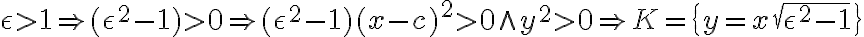 - dostali sme zjednotenie rôznobežiek.
- dostali sme zjednotenie rôznobežiek.