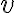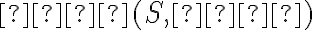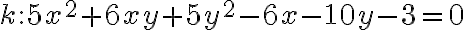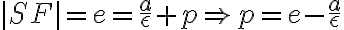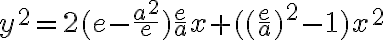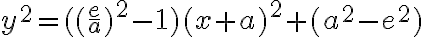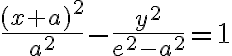Kubovčík, M.: Kužeľosečky
| Portál: | Virtuálna Univerzita Mateja Bela |
| Kurz: | Didaktika matematiky |
| Kniha: | Kubovčík, M.: Kužeľosečky |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | streda, 3 júla 2024, 13:22 |
Opis
Študijný materiál v elektronickej podobe bol vytvorený v rámci diplomovej práce Tvorba študijných materiálov z geometrie pre budúcich učiteľov matematiky. Čitateľ v ňom nájde problematiku kvadratických geometrických útvarov (kužeľosečiek), ktoré sú skúmané syntetickou a analytickou metódou.
1. Elipsa
Majme dva rôzne body roviny  . Označne vzdialenosť týchto bodov reálnym číslo
. Označne vzdialenosť týchto bodov reálnym číslo  .
.
Elipsa je množina všetkých bodov roviny , ktoré majú rovnaký súčet vzdialeností
, ktoré majú rovnaký súčet vzdialeností
od týchto dvoch pevne zvolených bodov a tento súčet je väčší, ako vzdialenosť týchto bodov:
a tento súčet je väčší, ako vzdialenosť týchto bodov:
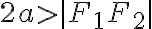
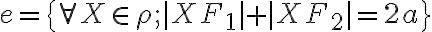
 . Označne vzdialenosť týchto bodov reálnym číslo
. Označne vzdialenosť týchto bodov reálnym číslo 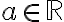 .
. Elipsa je množina všetkých bodov roviny
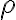 , ktoré majú rovnaký súčet vzdialeností
, ktoré majú rovnaký súčet vzdialeností od týchto dvoch pevne zvolených bodov
 a tento súčet je väčší, ako vzdialenosť týchto bodov:
a tento súčet je väčší, ako vzdialenosť týchto bodov: 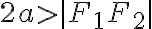
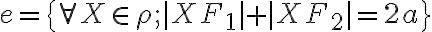
Priamky prechádzajúce ľubovoľným bodom elipsy  a jej ohniskami
a jej ohniskami 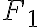 alebo
alebo 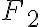 sa nazývajú sprievodiče bodu
sa nazývajú sprievodiče bodu  .
.
Sprievodiče bodu tvoria dva uhly so spoločným
vrcholom v bode
tvoria dva uhly so spoločným
vrcholom v bode  .
.
Vnútorným uhlom sprievodičov nazývame taký uhol, v ktorom leží stred elipsy , vo vonkajšom uhle sprievodičov ležia hlavné vrcholy elipsy
, vo vonkajšom uhle sprievodičov ležia hlavné vrcholy elipsy 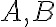 .
.
 a jej ohniskami
a jej ohniskami 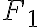 alebo
alebo 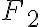 sa nazývajú sprievodiče bodu
sa nazývajú sprievodiče bodu  .
. Sprievodiče bodu
 tvoria dva uhly so spoločným
vrcholom v bode
tvoria dva uhly so spoločným
vrcholom v bode  .
.Vnútorným uhlom sprievodičov nazývame taký uhol, v ktorom leží stred elipsy
 , vo vonkajšom uhle sprievodičov ležia hlavné vrcholy elipsy
, vo vonkajšom uhle sprievodičov ležia hlavné vrcholy elipsy 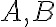 .
.
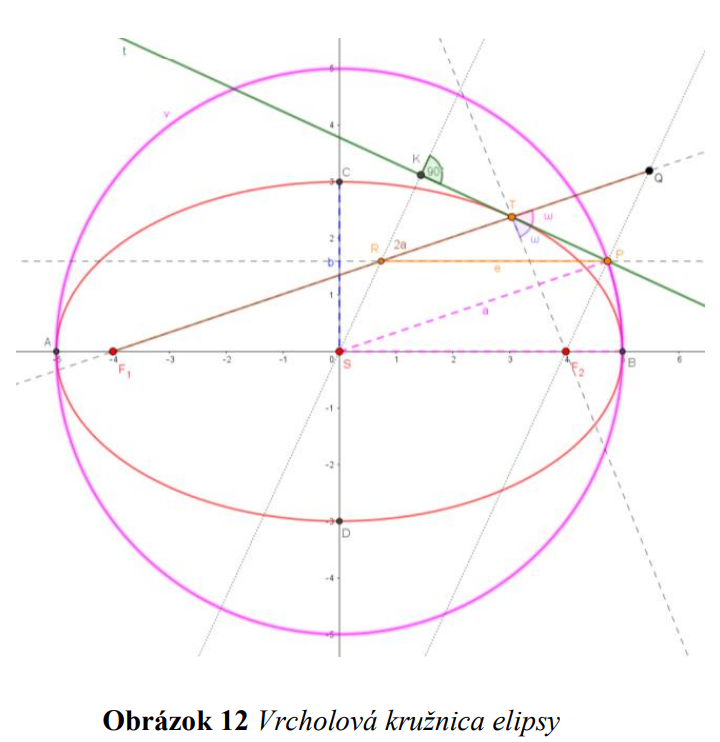
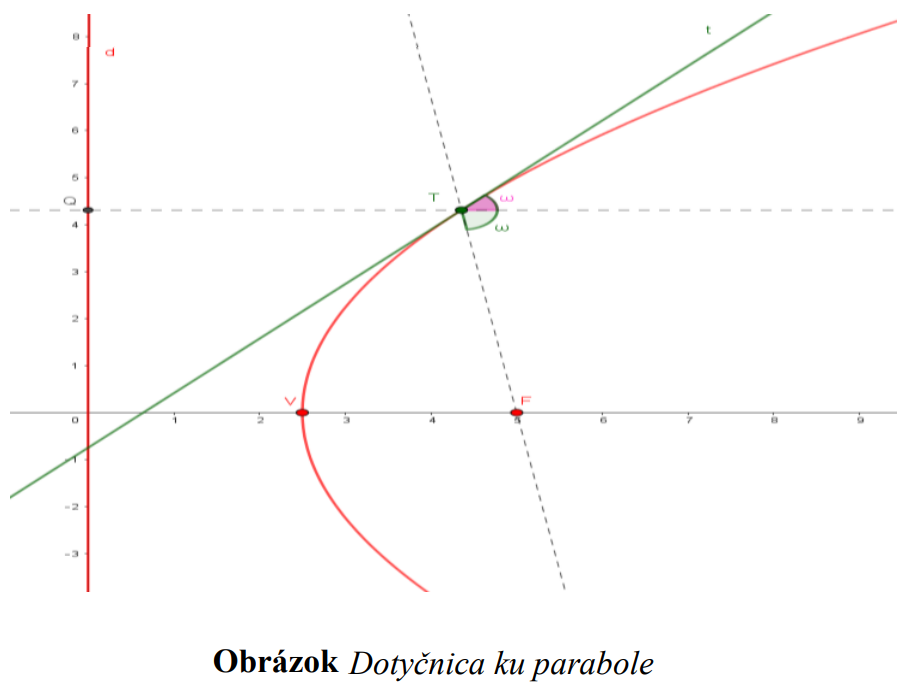
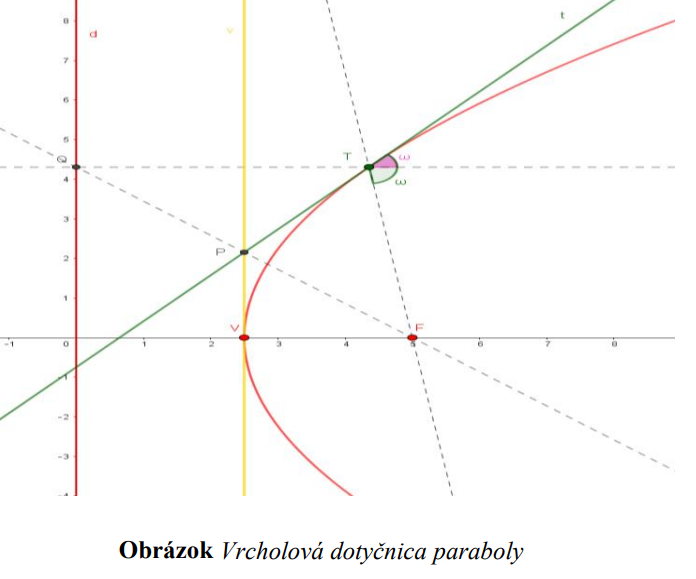
Priamka 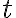 je dotyčnicou ku elipse v dotykovom bode
je dotyčnicou ku elipse v dotykovom bode 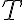 práve vtedy,
práve vtedy,
keď je osou vonkajšieho uhla 𝜔 sprievodičov bodu dotyku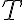 .
.
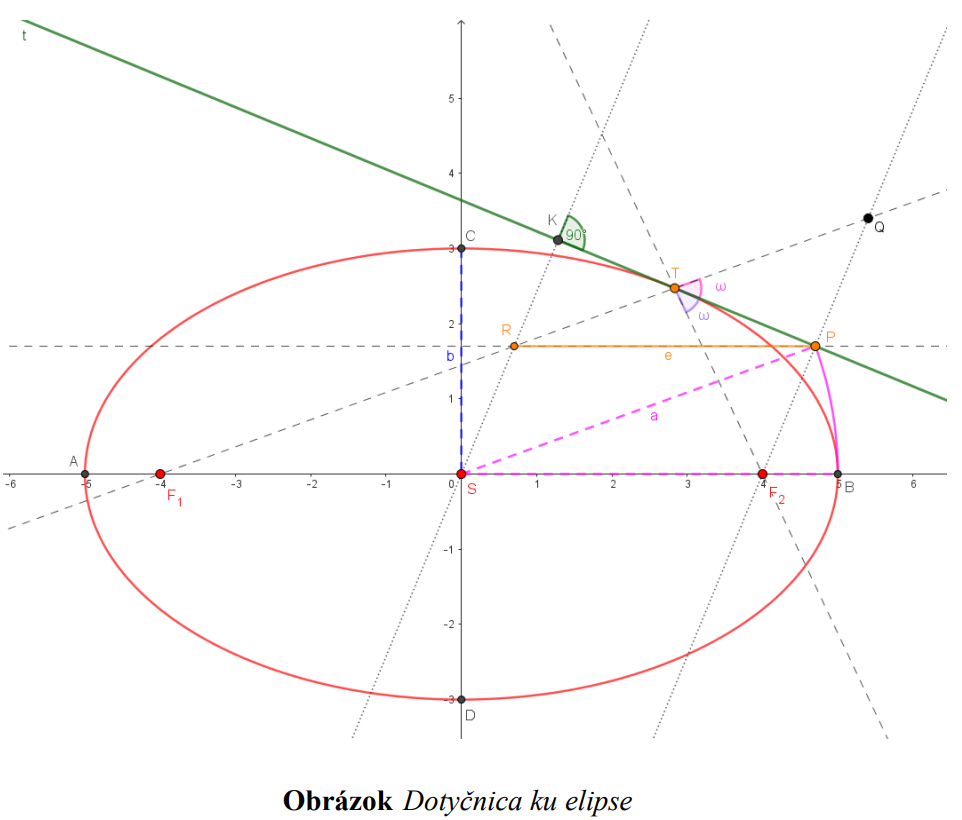
 je dotyčnicou ku elipse v dotykovom bode
je dotyčnicou ku elipse v dotykovom bode  práve vtedy,
práve vtedy,keď je osou vonkajšieho uhla 𝜔 sprievodičov bodu dotyku
 .
. 
Združené priemery elipsy nazývame také dva priemery elipsy, pre ktoré platí,
že dotyčnice v krajných bodoch jedného priemeru sú rovnobežné s priemerom k nemu združenému.
že dotyčnice v krajných bodoch jedného priemeru sú rovnobežné s priemerom k nemu združenému.
Riadiace kružnice elipsy 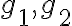 sú množiny bodov súmerných s jedným ohniskom elipsy podľa všetkých dotyčníc ku elipse,
sú množiny bodov súmerných s jedným ohniskom elipsy podľa všetkých dotyčníc ku elipse,
pričom stred tejto kružnice je v druhom ohnisku a polomer kružnice je o veľkosti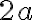 :
:
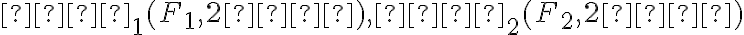 .
.
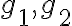 sú množiny bodov súmerných s jedným ohniskom elipsy podľa všetkých dotyčníc ku elipse,
sú množiny bodov súmerných s jedným ohniskom elipsy podľa všetkých dotyčníc ku elipse,
pričom stred tejto kružnice je v druhom ohnisku a polomer kružnice je o veľkosti
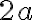 :
: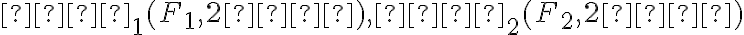 .
.
1.1. Konštrukcia elipsy
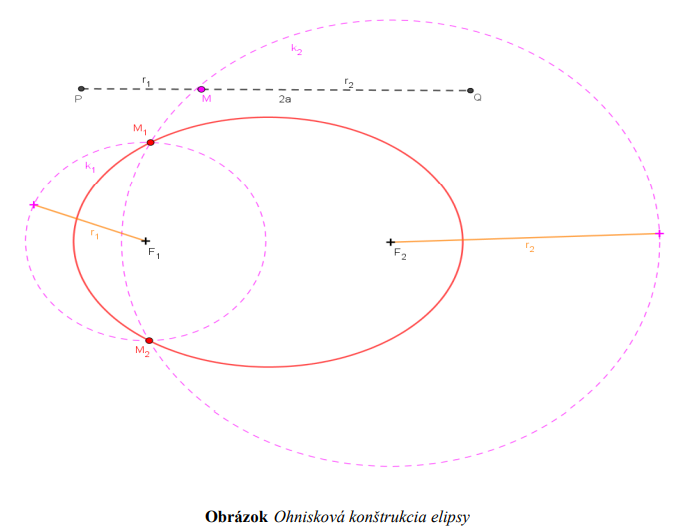
Ohnisková (bodová) konštrukcia:
najprv zostrojíme úsečku 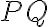 o veľkosti \2a\) a na nej si zvolíme ľubovoľný bod
o veľkosti \2a\) a na nej si zvolíme ľubovoľný bod 
potom zostrojíme tzv. hyperoskulačné kružnice 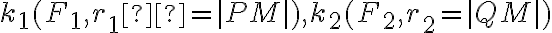
takto získame body 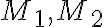 patriace hľadanej elipsy ako prienik hyperoskulačných kružníc
patriace hľadanej elipsy ako prienik hyperoskulačných kružníc
ďalšie body elipsy získame podobným postupom ľubovoľnou voľbou bodu  na úsečke
na úsečke 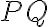
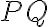 o veľkosti \2a\) a na nej si zvolíme ľubovoľný bod
o veľkosti \2a\) a na nej si zvolíme ľubovoľný bod 
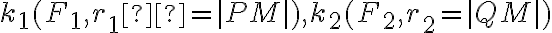
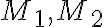 patriace hľadanej elipsy ako prienik hyperoskulačných kružníc
patriace hľadanej elipsy ako prienik hyperoskulačných kružníc
 na úsečke
na úsečke 
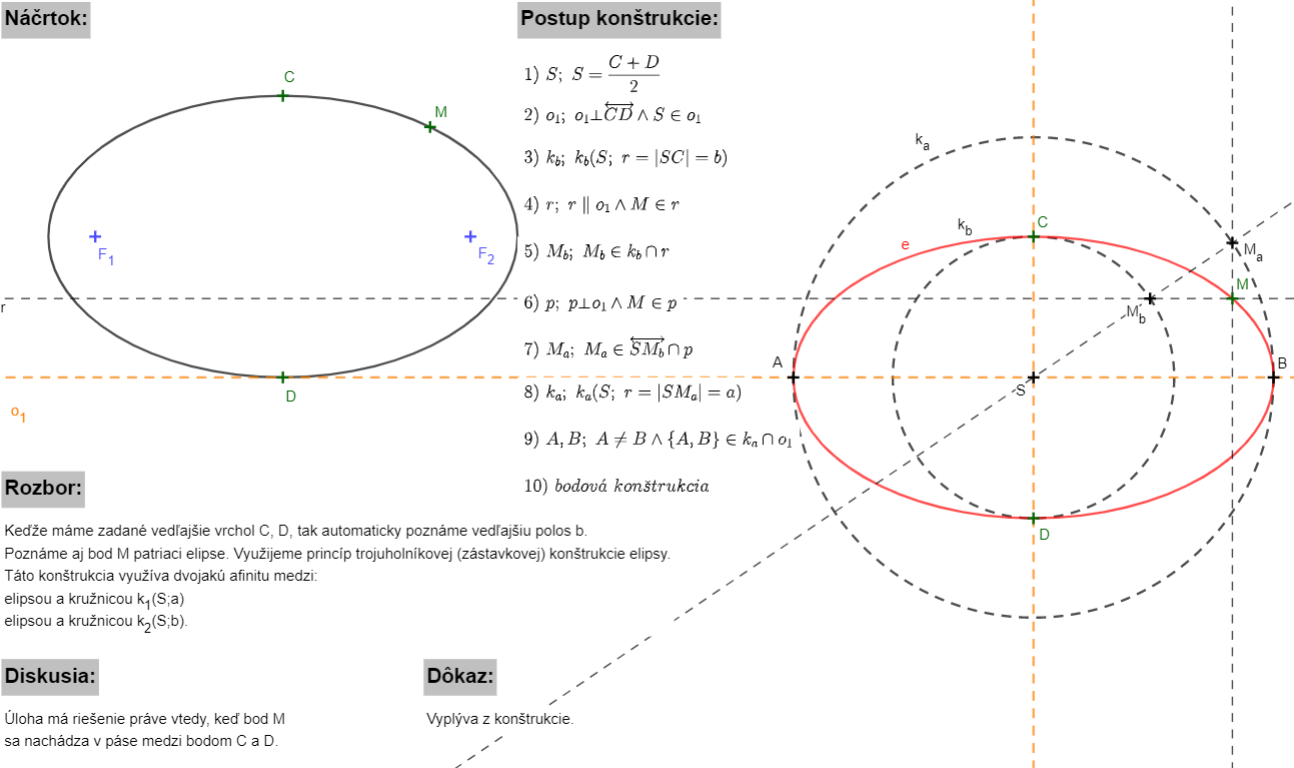
Trojuholníková (zástavková) konštrukcia:
- využívame vtedy, ak máme zadané stred elipsy
 , veľkosti hlavnej a vedľajšej polosi
, veľkosti hlavnej a vedľajšej polosi 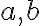 , hlavnú a vedľajšiu os
, hlavnú a vedľajšiu os 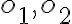
- zostrojíme sústredné kružnice
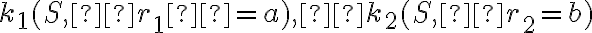
- vedieme ľubovoľnú priamku p prechádzajúcu stredom elipsy

- získame priesečníky polpriamky a sústredných kružníc:
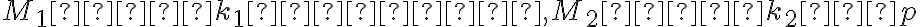
- zostrojíme takéto priamky
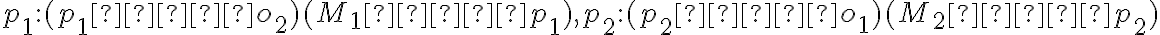
- získame bod elipsy
 ako priesečník zostrojených priamok:
ako priesečník zostrojených priamok: 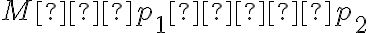
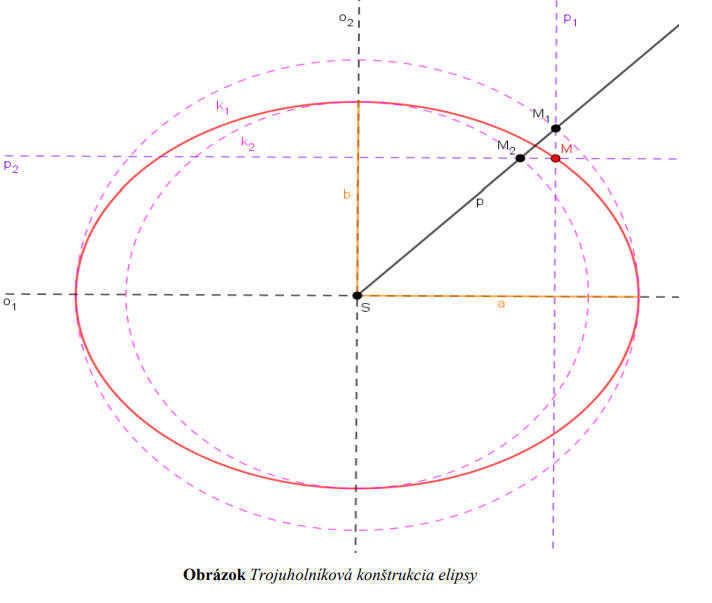
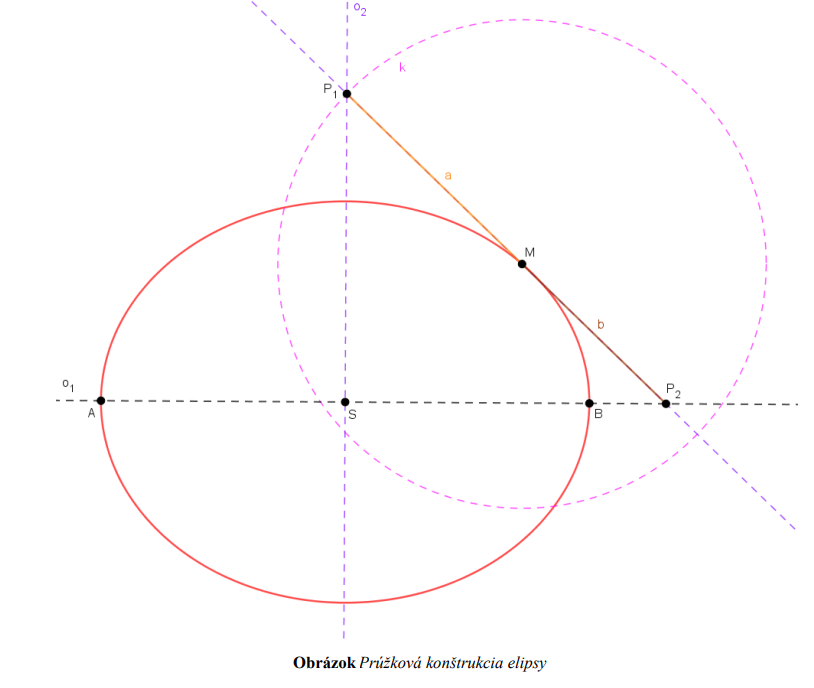
Prúžková konštrukcia:
- využívame vtedy, ak máme zadanú hlavnú os
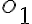 , hlavné vrcholy
, hlavné vrcholy 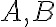 a bod
a bod  , ktorý patrí elipse, ale nie je vrcholom tejto elipsy
, ktorý patrí elipse, ale nie je vrcholom tejto elipsy
- nájdeme stred elipsy
 ako stred úsečky
ako stred úsečky 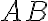
- takto poznáme veľkosť hlavnej polosi
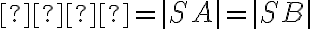 , teraz nám stačí nájsť veľkosť vedľajšej polosi
, teraz nám stačí nájsť veľkosť vedľajšej polosi 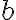
- najprv zostrojíme vedľajšiu os
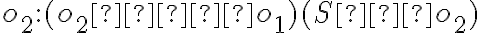
- potom zostrojíme kružnicu
 so stredom v bode
so stredom v bode  a polomerom
a polomerom 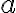 , t. j.
, t. j. 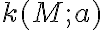
- získame priesečník
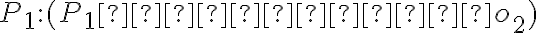
- zostrojíme priamku
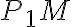 a získame priesečník
a získame priesečník 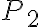 tejto priamky a hlavnej osi
tejto priamky a hlavnej osi
- hľadaná veľkosť vedľajšej polosi
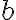 je
je 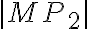
- obdobne postupujeme, keď poznáme vedľajšie vrcholy
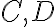 , s rozdielom, že hľadáme veľkosť hlavnej polosi
, s rozdielom, že hľadáme veľkosť hlavnej polosi 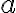
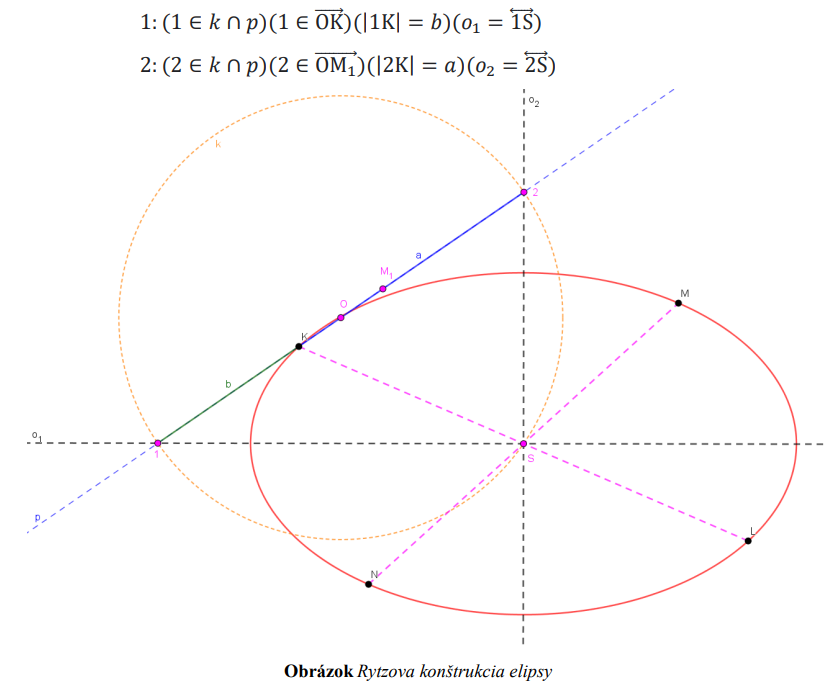
Rytzova konštrukcia:
- využívame vtedy, keď poznáme združené priemery elipsy
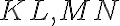
- keďže združené priemery sa pretínajú v strede elipsy, tak najprv nájdeme tento stred elipsy
 , a potom otočíme bod
, a potom otočíme bod  o
o 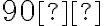 okolo bodu
okolo bodu  , t. j.
, t. j. 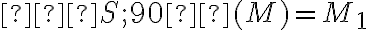
- nájdeme bod
 ako stred úsečky
ako stred úsečky 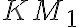
- zostrojíme kružnicu \(𝑘(O; r = |OS|)\)a priamku
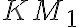
- získame priesečníky
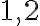 kružnice
kružnice  a priamky
a priamky 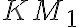 také, pre ktoré platí:
také, pre ktoré platí:
1.2. Konštrukčné úlohy na elipsu
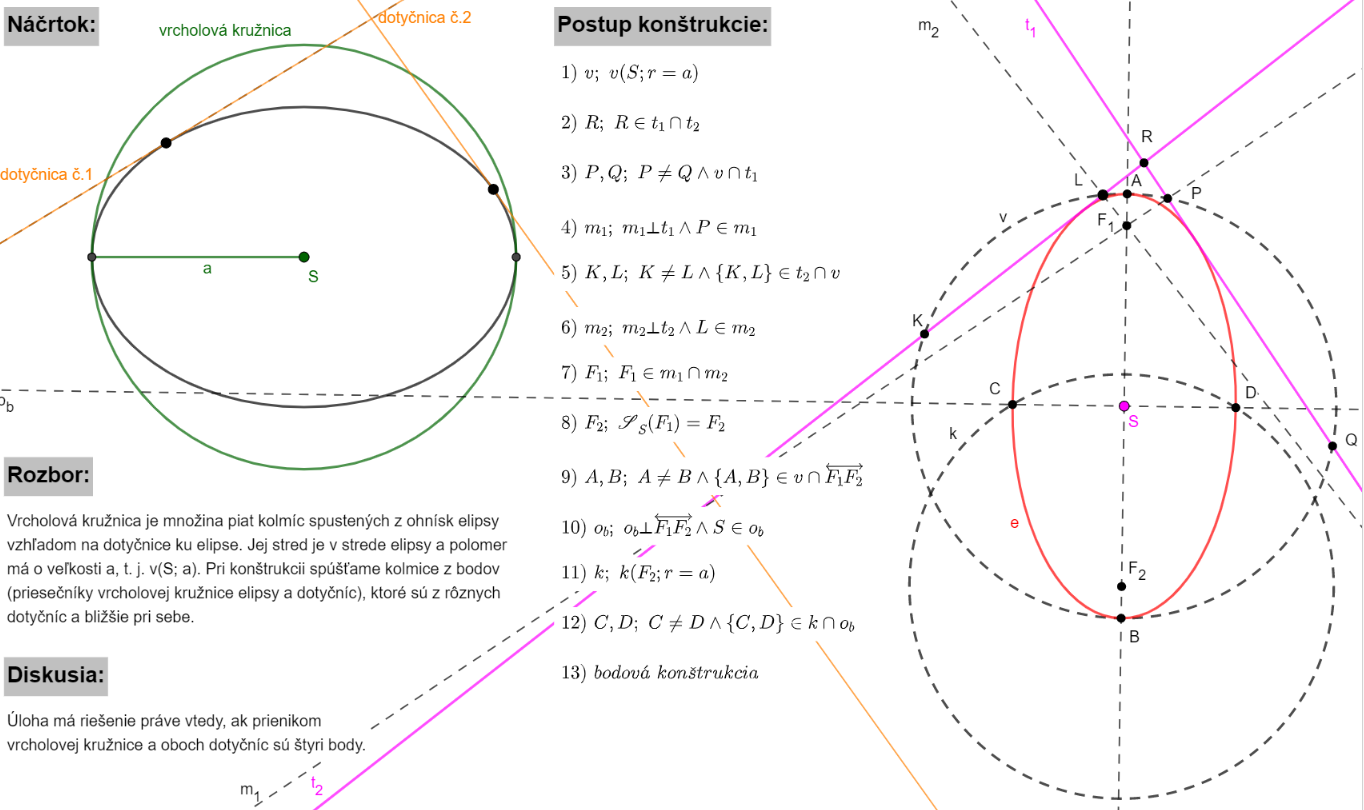
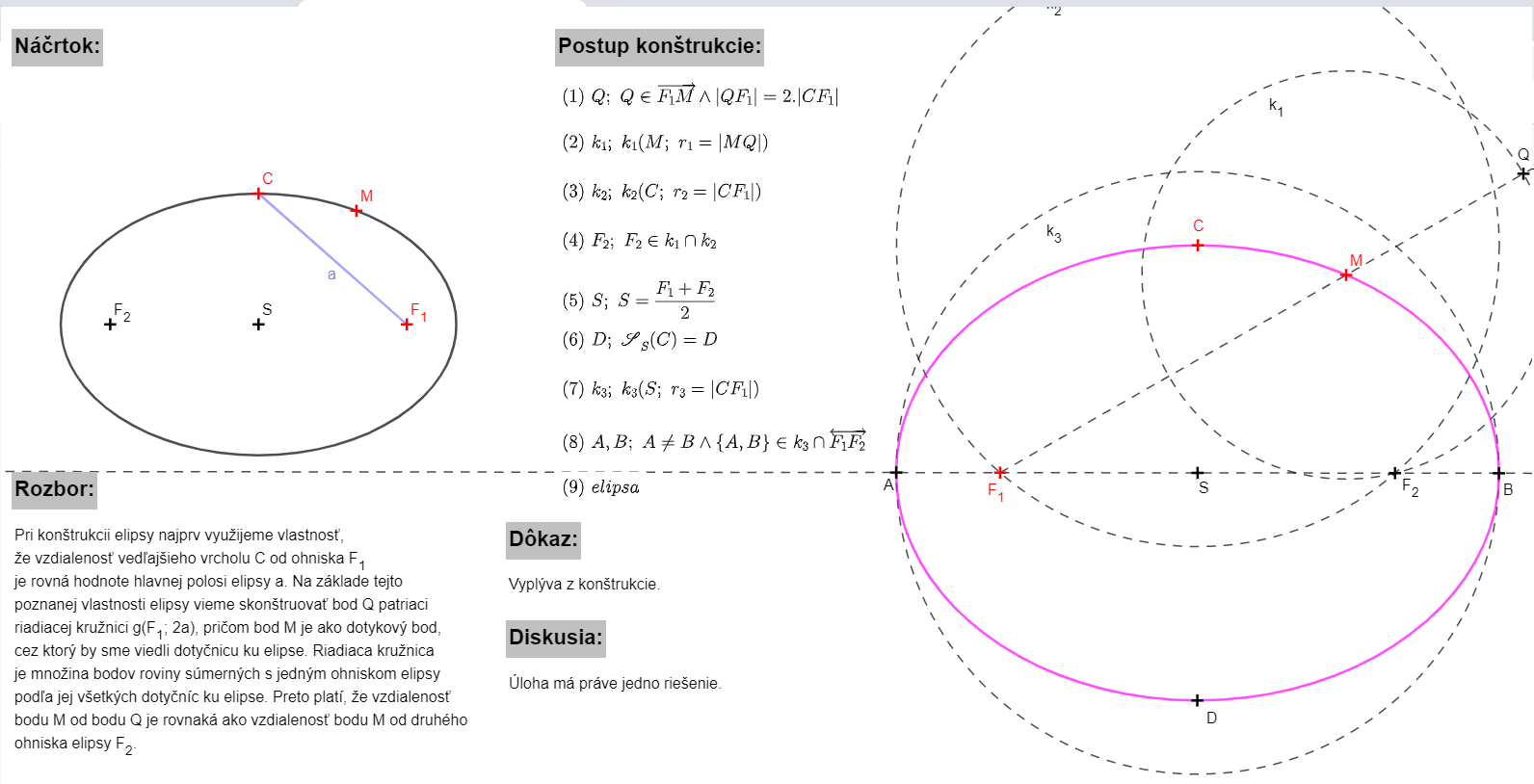
Príklad 1: Zostrojte elipsu, ak sú dané jej dve dotyčnice  , stred elipsy
, stred elipsy  a hlavná polos
a hlavná polos 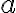 .
Riešenie príkladu v GeoGebre.
.
Riešenie príkladu v GeoGebre.
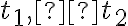 , stred elipsy
, stred elipsy  a hlavná polos
a hlavná polos 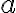 .
Riešenie príkladu v GeoGebre.
.
Riešenie príkladu v GeoGebre.

Príklad 2: Zostrojte elipsu, ak je dané ohnisko 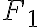 , vedľajší vrchol
, vedľajší vrchol  a bod
a bod  patriaci elipse. Riešenie príkladu v GeoGebre.
patriaci elipse. Riešenie príkladu v GeoGebre.
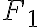 , vedľajší vrchol
, vedľajší vrchol  a bod
a bod  patriaci elipse. Riešenie príkladu v GeoGebre.
patriaci elipse. Riešenie príkladu v GeoGebre.

Príklad 3: Zostrojte elipsu, ak sú dané jej vedľajšie vrcholy  a bod
a bod  patriaci tejto elipse. Riešenie príkladu v GeoGebre.
patriaci tejto elipse. Riešenie príkladu v GeoGebre.
 a bod
a bod  patriaci tejto elipse. Riešenie príkladu v GeoGebre.
patriaci tejto elipse. Riešenie príkladu v GeoGebre.

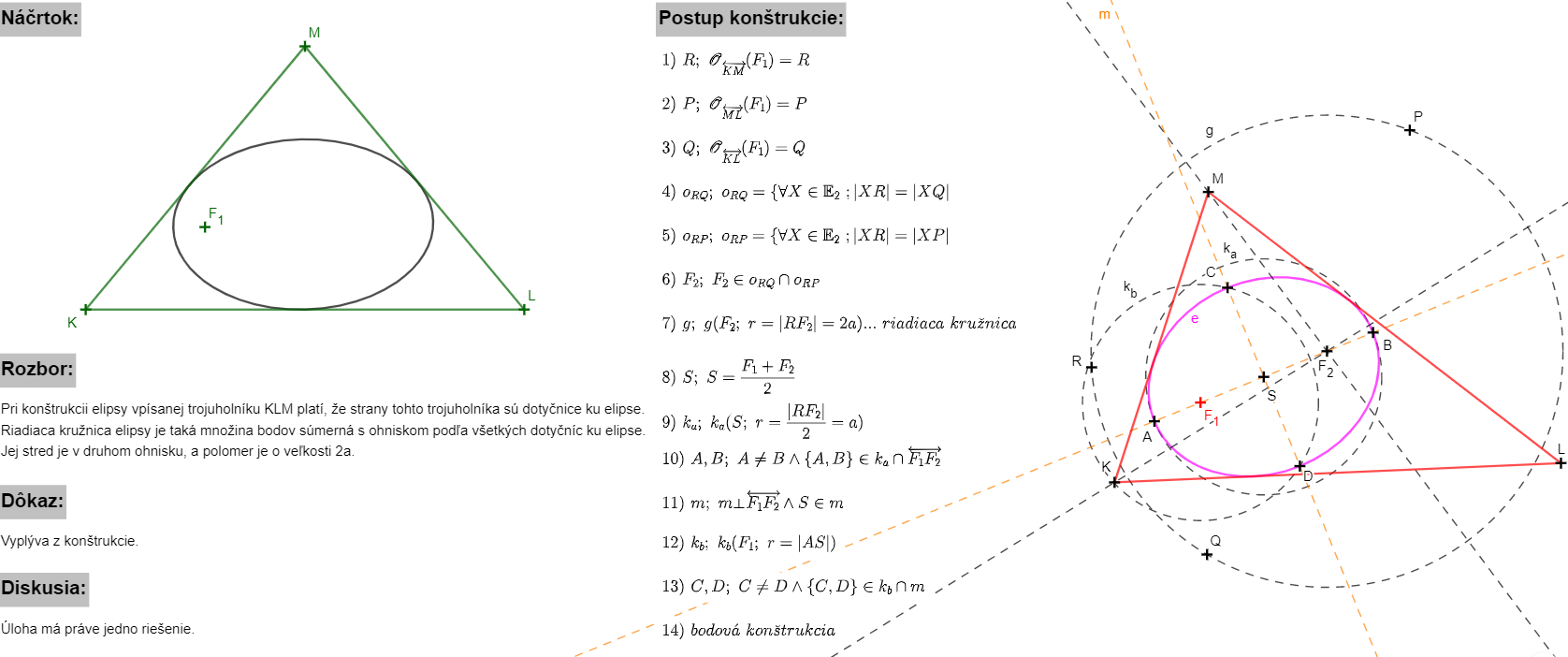
Príklad 4: Daný je trojuholník 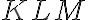 a jeho vnútorný bod
a jeho vnútorný bod 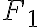 . Zostrojte elipsu vpísanú trojuholníku
. Zostrojte elipsu vpísanú trojuholníku 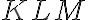 tak,
aby bod
tak,
aby bod 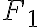 bol jej ohniskom. Riešenie úlohy v GeoGebre.
bol jej ohniskom. Riešenie úlohy v GeoGebre.
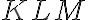 a jeho vnútorný bod
a jeho vnútorný bod 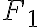 . Zostrojte elipsu vpísanú trojuholníku
. Zostrojte elipsu vpísanú trojuholníku 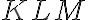 tak,
aby bod
tak,
aby bod 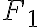 bol jej ohniskom. Riešenie úlohy v GeoGebre.
bol jej ohniskom. Riešenie úlohy v GeoGebre.

2. Hyperbola
Majme dva rôzne body roviny  a reálne číslo
a reálne číslo 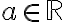 .
.
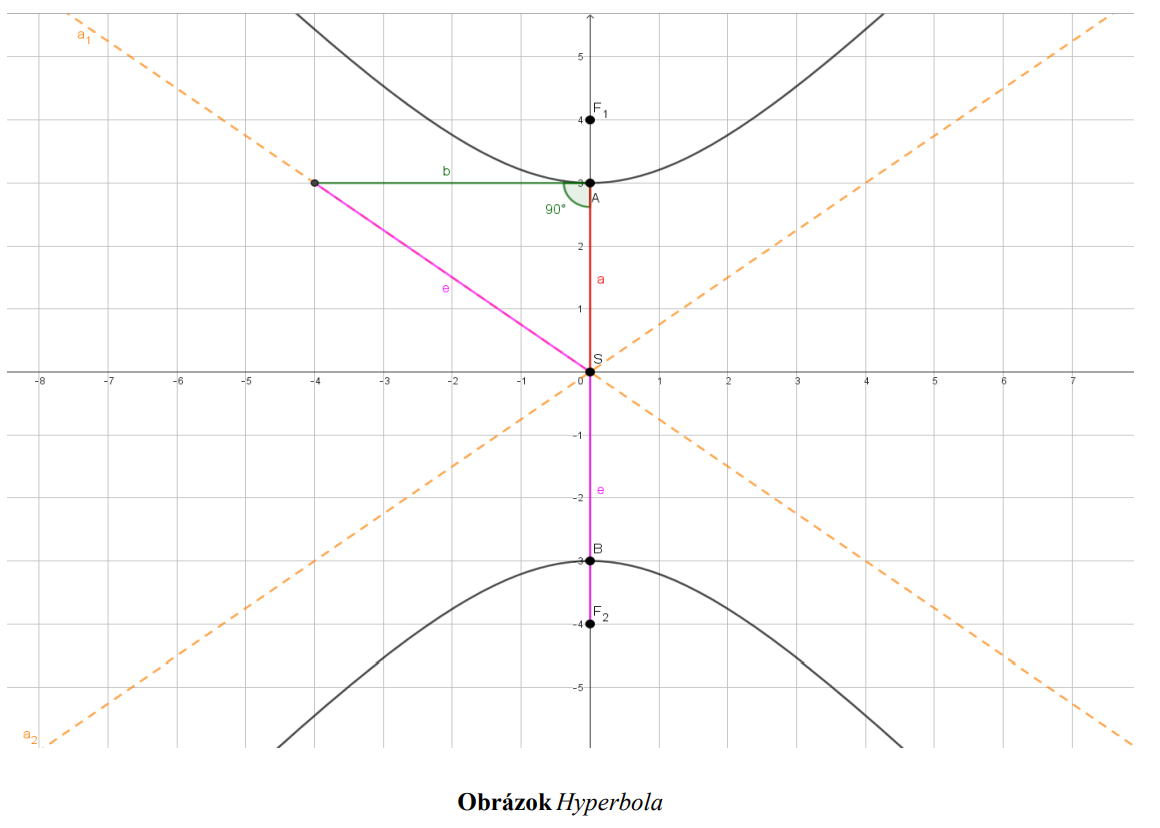
Hyperbola ℌ je množina všetkých bodov v rovine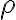 , ktoré majú rovnaký rozdiel vzdialeností
, ktoré majú rovnaký rozdiel vzdialeností
od týchto dvoch zvolených bodov a tento absolútny rozdiel je menší, ako je vzdialenosť ohnísk:
a tento absolútny rozdiel je menší, ako je vzdialenosť ohnísk:
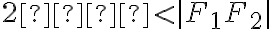
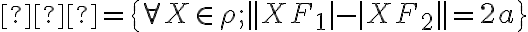
 a reálne číslo
a reálne číslo 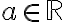 .
.
Hyperbola ℌ je množina všetkých bodov v rovine
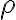 , ktoré majú rovnaký rozdiel vzdialeností
, ktoré majú rovnaký rozdiel vzdialeností
od týchto dvoch zvolených bodov
 a tento absolútny rozdiel je menší, ako je vzdialenosť ohnísk:
a tento absolútny rozdiel je menší, ako je vzdialenosť ohnísk:
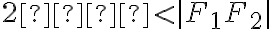
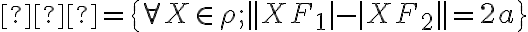

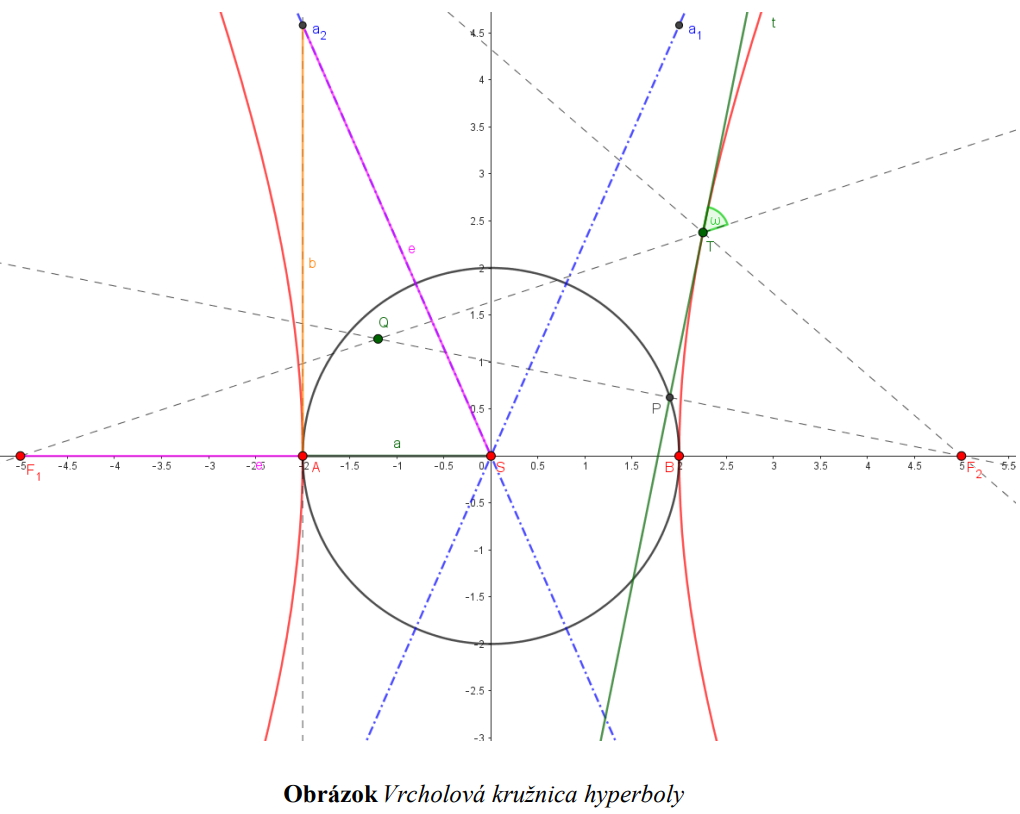
Asymptoty hyperboly 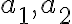 sú priamky, ktoré prechádzajú stredom hyperboly
sú priamky, ktoré prechádzajú stredom hyperboly 
a zvierajú s hlavnou osou hyperboly uhol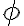 , pre ktorý platí
, pre ktorý platí 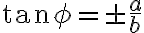 .
.
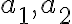 sú priamky, ktoré prechádzajú stredom hyperboly
sú priamky, ktoré prechádzajú stredom hyperboly 
a zvierajú s hlavnou osou hyperboly uhol
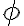 , pre ktorý platí
, pre ktorý platí 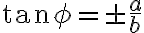 .
.

Priamky prechádzajúce ľubovoľným bodom hyperboly  a jej ohniskami
a jej ohniskami 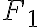 alebo
alebo 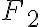 sa nazývajú sprievodiče bodu
sa nazývajú sprievodiče bodu  .
.
Sprievodiče bodu tvoria dva uhly so spoločným vrcholom v bode
tvoria dva uhly so spoločným vrcholom v bode  .
.
Vnútorným uhlom sprievodičov nazývame taký uhol, v ktorom ležia ohniská hyperboly , inak ide o vonkajší uhol sprievodičov.
, inak ide o vonkajší uhol sprievodičov.
 a jej ohniskami
a jej ohniskami 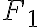 alebo
alebo 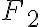 sa nazývajú sprievodiče bodu
sa nazývajú sprievodiče bodu  .
.
Sprievodiče bodu
 tvoria dva uhly so spoločným vrcholom v bode
tvoria dva uhly so spoločným vrcholom v bode  .
.
Vnútorným uhlom sprievodičov nazývame taký uhol, v ktorom ležia ohniská hyperboly
 , inak ide o vonkajší uhol sprievodičov.
, inak ide o vonkajší uhol sprievodičov.
Priamka 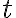 je dotyčnicou ku hyperbole v dotykovom bode
je dotyčnicou ku hyperbole v dotykovom bode 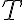 práve vtedy, keď je osou vonkajšieho uhla
práve vtedy, keď je osou vonkajšieho uhla 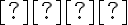 sprievodičov bodu dotyku
sprievodičov bodu dotyku 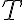 .
.
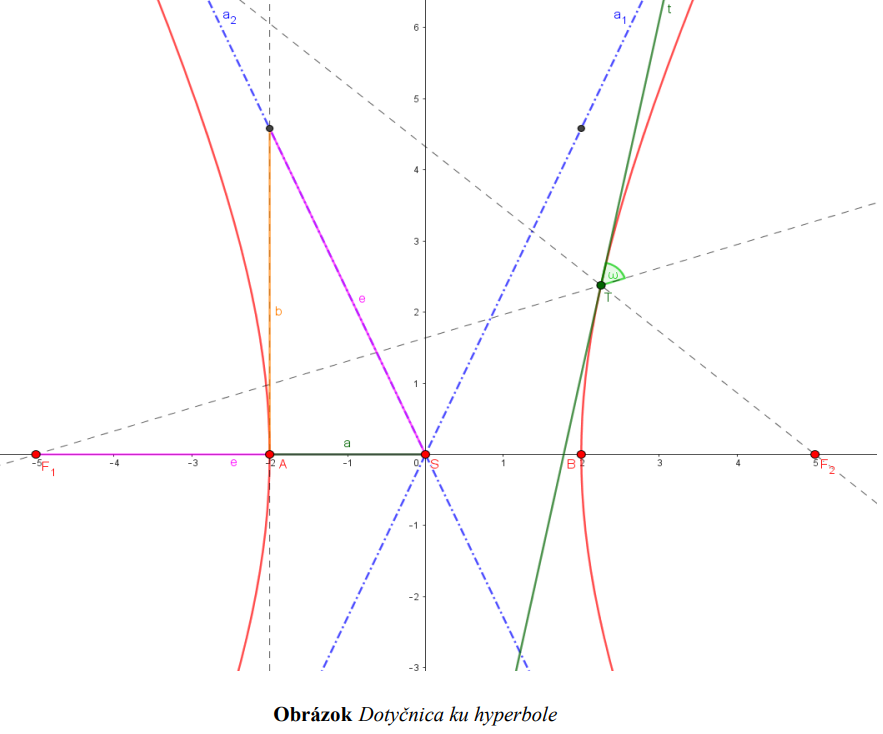
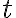 je dotyčnicou ku hyperbole v dotykovom bode
je dotyčnicou ku hyperbole v dotykovom bode 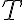 práve vtedy, keď je osou vonkajšieho uhla
práve vtedy, keď je osou vonkajšieho uhla 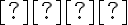 sprievodičov bodu dotyku
sprievodičov bodu dotyku 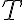 .
.

Riadiace kružnice hyperboly 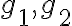 sú množiny bodov súmerných s jedným ohniskom hyperboly
sú množiny bodov súmerných s jedným ohniskom hyperboly
podľa všetkých dotyčníc ku hyperbole, pričom stred tejto kružnice je v druhom ohnisku a polomer kružnice je o veľkosti 2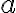 :
:
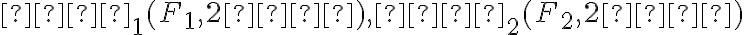 .
.
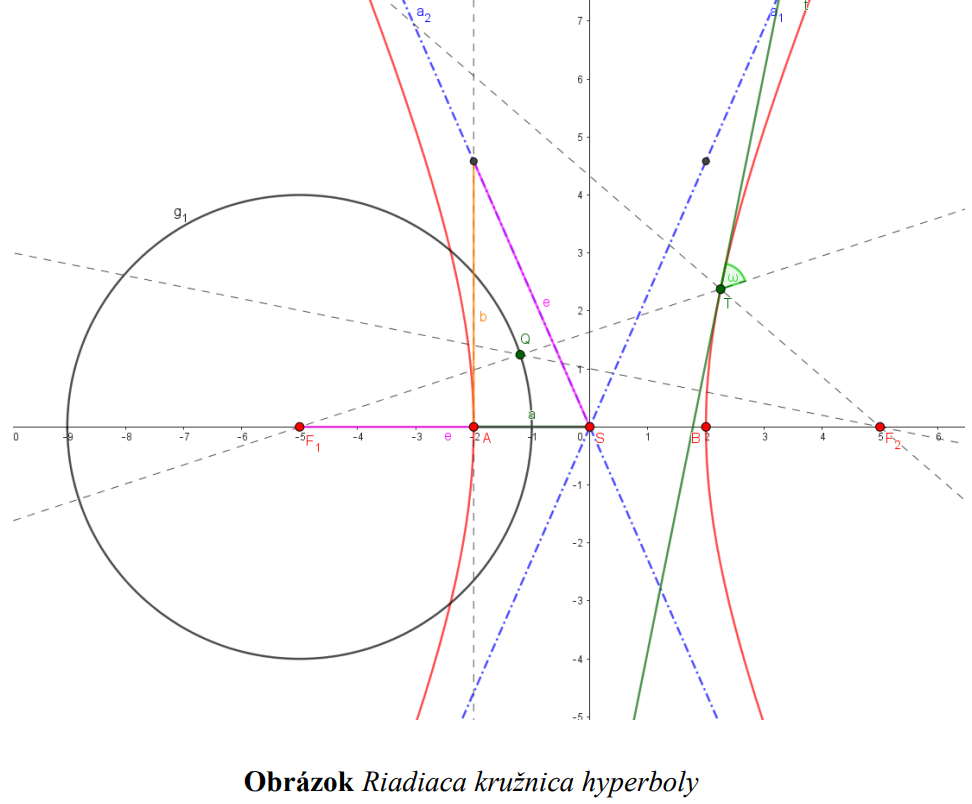
 sú množiny bodov súmerných s jedným ohniskom hyperboly
sú množiny bodov súmerných s jedným ohniskom hyperboly
podľa všetkých dotyčníc ku hyperbole, pričom stred tejto kružnice je v druhom ohnisku a polomer kružnice je o veľkosti 2
 :
:
 .
.

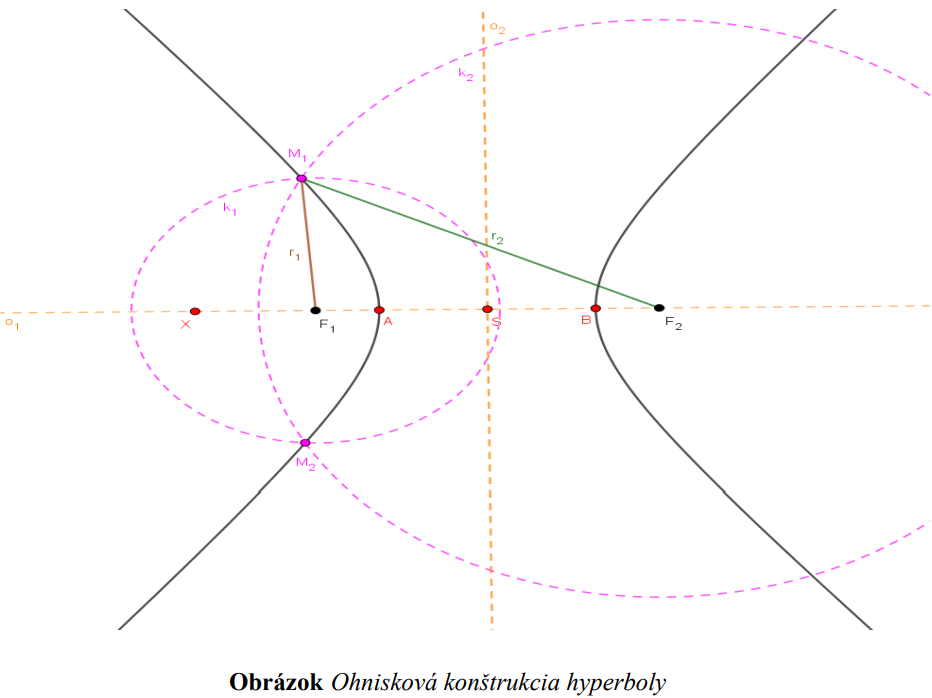
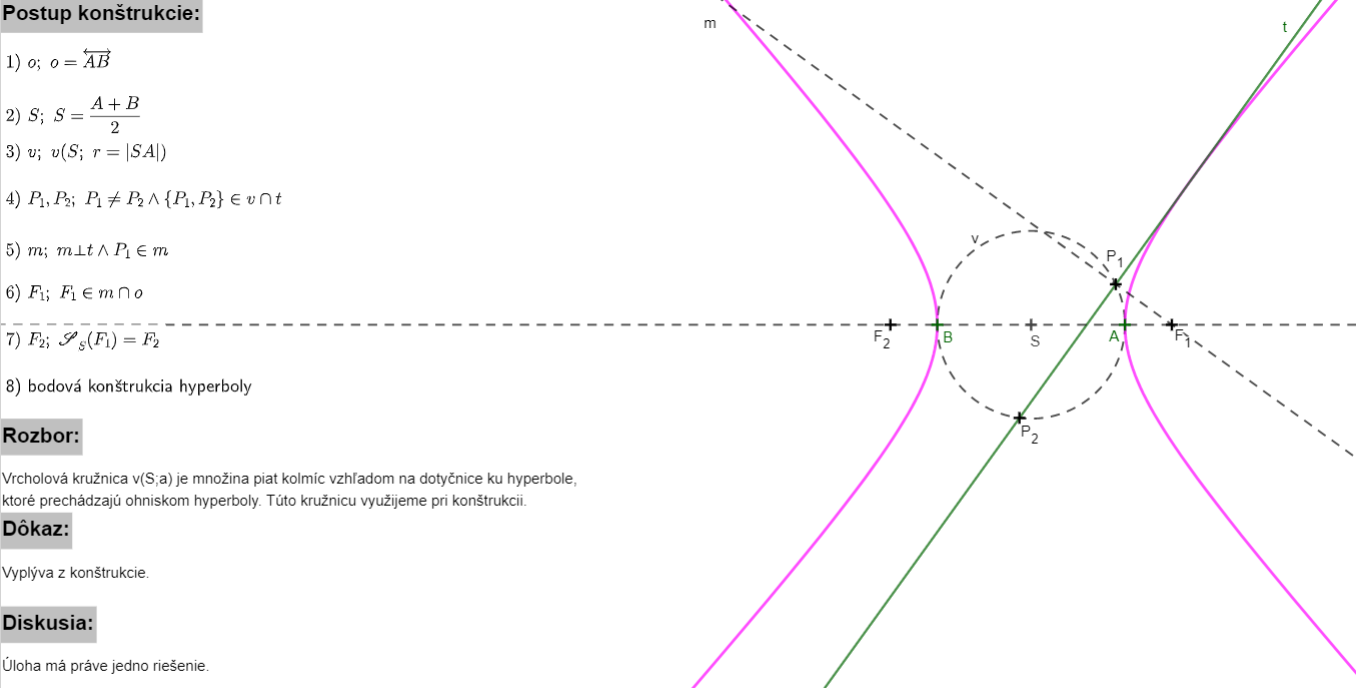
2.1. Konštrukcia hyperboly
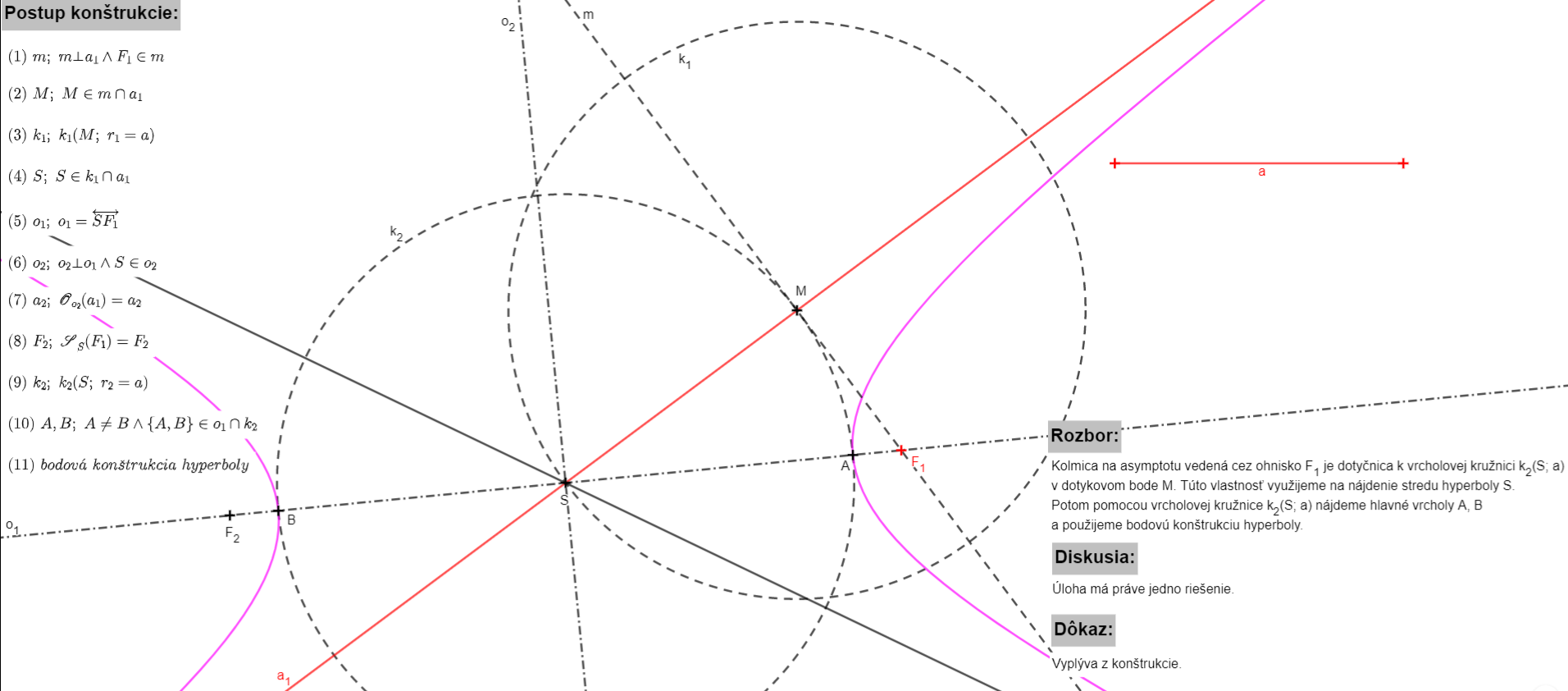
Ohnisková (bodová) konštrukcia:
- využívame vtedy, ak máme zadané
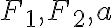
- nájdeme stred hyperboly
 ako stred úsečky
ako stred úsečky 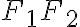
- zostrojíme kružnicu
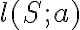 a hlavné vrcholy
a hlavné vrcholy 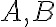 nájdeme ako priesečník kružnice
nájdeme ako priesečník kružnice 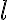 a priamky
a priamky 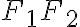
- zvolíme si ľubovoľný bod
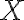 na priamke
na priamke 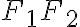
- potom zostrojíme kružnice
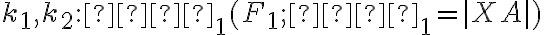 ,
, 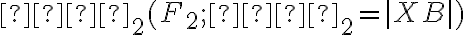
- nájdeme body
 patriace hyperbole ako priesečníky kružníc
patriace hyperbole ako priesečníky kružníc 
2.2. Konštrukčné úlohy na hyperbolu
Príklad 1: Zostrojte hyperbolu, ak sú dané jej dva hlavné vrcholy 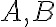 a dotyčnica ku hyperbole
a dotyčnica ku hyperbole 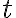 . Riešenie príkladu v GeoGebre.
. Riešenie príkladu v GeoGebre.
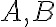 a dotyčnica ku hyperbole
a dotyčnica ku hyperbole 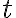 . Riešenie príkladu v GeoGebre.
. Riešenie príkladu v GeoGebre.
Príklad 2: Zostrojte hyperbolu, ak je daná jej asymptota 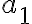 , ohnisko
, ohnisko 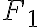 a hlavná polos
a hlavná polos 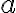 . Riešenie príkladu v GeoGebre.
. Riešenie príkladu v GeoGebre.
 , ohnisko
, ohnisko  a hlavná polos
a hlavná polos 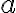 . Riešenie príkladu v GeoGebre.
. Riešenie príkladu v GeoGebre.
Príklad 3: Zostrojte hyperbolu, ak je daná hlavná os  , na nej ohnisko
, na nej ohnisko  , lineárna excentricita
, lineárna excentricita 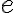 a bod
a bod  patriaci hyperbole. Riešenie príkladu v GeoGebre.
patriaci hyperbole. Riešenie príkladu v GeoGebre.
 , na nej ohnisko
, na nej ohnisko  , lineárna excentricita
, lineárna excentricita 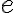 a bod
a bod  patriaci hyperbole. Riešenie príkladu v GeoGebre.
patriaci hyperbole. Riešenie príkladu v GeoGebre.
3. Parabola
Majme bod roviny  a priamku
a priamku  ležiacu v tejto rovine
ležiacu v tejto rovine 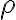 , pričom
, pričom  .
.
Parabola je množina všetkých bodov v rovine
je množina všetkých bodov v rovine 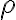 ,
,
ktoré majú rovnakú vzdialenosť od danej priamky a pevne zvoleného bodu
a pevne zvoleného bodu  :
:
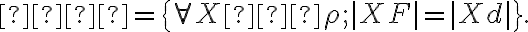
 a priamku
a priamku  ležiacu v tejto rovine
ležiacu v tejto rovine  , pričom
, pričom  .
.
Parabola
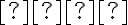 je množina všetkých bodov v rovine
je množina všetkých bodov v rovine 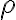 ,
,
ktoré majú rovnakú vzdialenosť od danej priamky
 a pevne zvoleného bodu
a pevne zvoleného bodu  :
:
Priamky prechádzajúce ľubovoľným bodom hyperboly  a jej ohniskom
a jej ohniskom  kolmicou prechádzajúcou bodom
kolmicou prechádzajúcou bodom 
vzhľadom na riadiacu priamku s priesečníkom
s priesečníkom 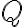 nazývame sprievodiče bodu
nazývame sprievodiče bodu  .
.
Sprievodiče bodu tvoria dva uhly so spoločným vrcholom v bode
tvoria dva uhly so spoločným vrcholom v bode  .
.
Vnútorným uhlom sprievodičov nazývame taký uhol, v ktorom leží ohnisko , inak ide o vonkajšie uhly sprievodičov.
, inak ide o vonkajšie uhly sprievodičov.
 a jej ohniskom
a jej ohniskom  kolmicou prechádzajúcou bodom
kolmicou prechádzajúcou bodom 
vzhľadom na riadiacu priamku
 s priesečníkom
s priesečníkom 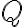 nazývame sprievodiče bodu
nazývame sprievodiče bodu  .
.
Sprievodiče bodu
 tvoria dva uhly so spoločným vrcholom v bode
tvoria dva uhly so spoločným vrcholom v bode  .
.
Vnútorným uhlom sprievodičov nazývame taký uhol, v ktorom leží ohnisko
 , inak ide o vonkajšie uhly sprievodičov.
, inak ide o vonkajšie uhly sprievodičov.
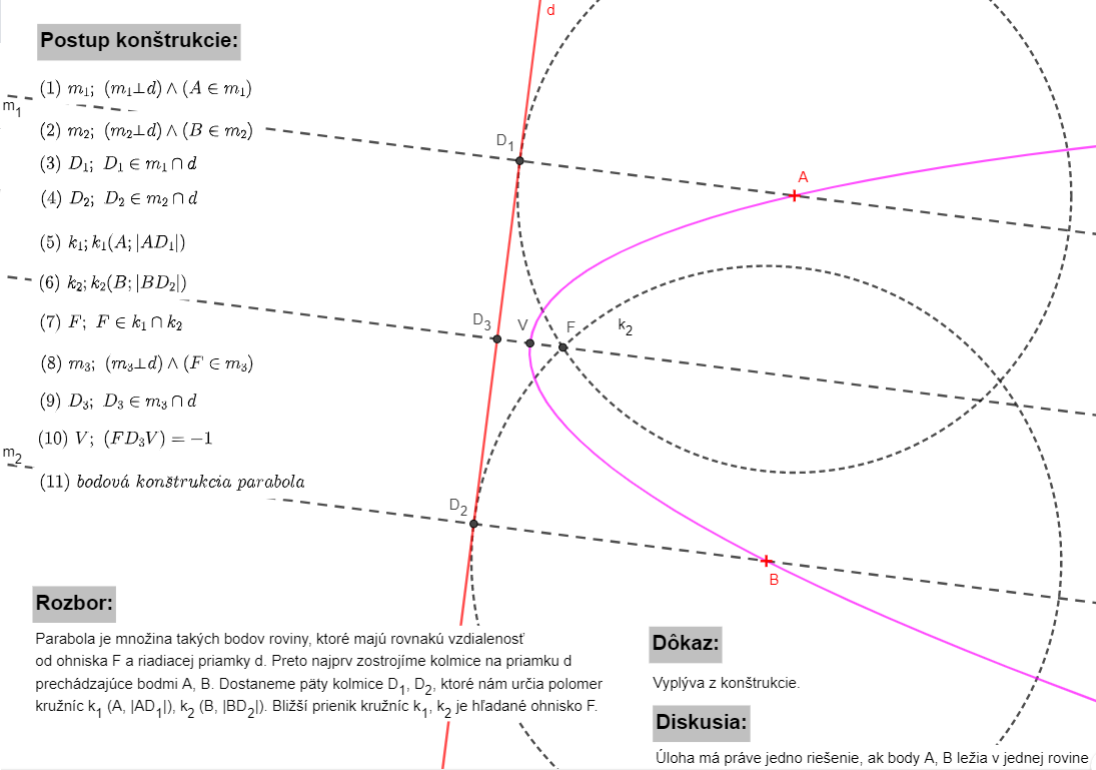
3.1. Konštrukcia paraboly
Teraz uvedieme ohniskovú (bodovú) konštrukciu paraboly, ktorá vychádza z predpokladu, že parabola je množina bodov danej vlastnosti:
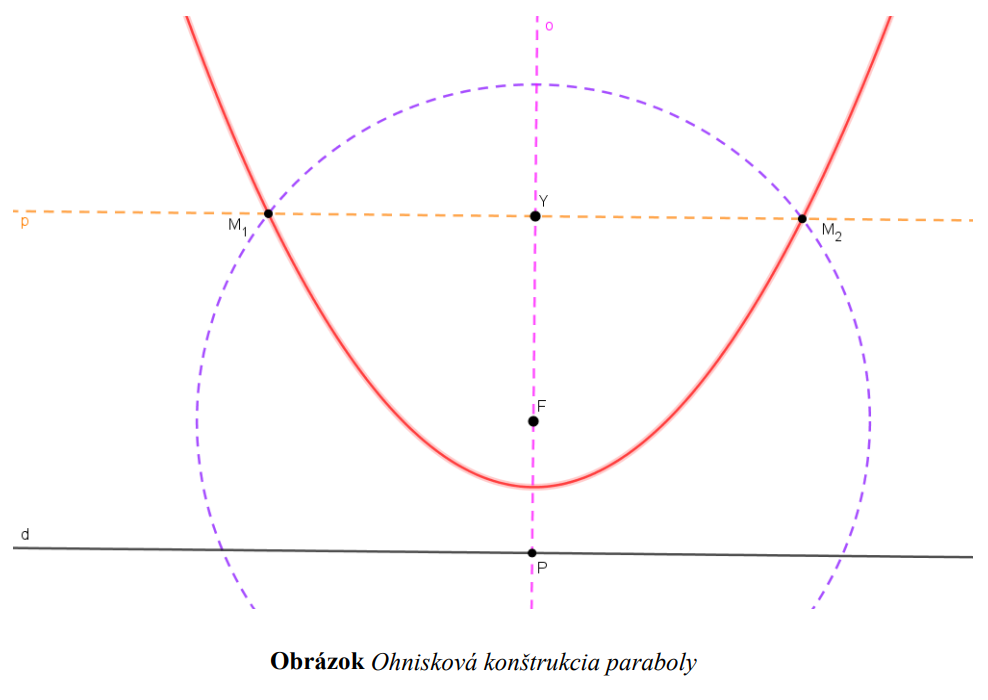
- využívame vtedy, keď poznáme ohnisko
 a riadiacu priamku
a riadiacu priamku 
- zostrojíme kolmicu
 na riadiacu priamku
na riadiacu priamku  prechádzajúcu cez ohnisko
prechádzajúcu cez ohnisko  , pätu tejto kolmice označíme
, pätu tejto kolmice označíme 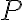
- na polpriamke
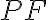 si zvolíme ľubovoľný bod
si zvolíme ľubovoľný bod 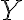
- cez bod
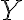 vedieme rovnobežnú priamku
vedieme rovnobežnú priamku  s riadiacou priamkou
s riadiacou priamkou 
- zostrojíme kružnicu
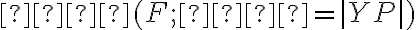
- hľadané body paraboly
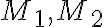 sú priesečníky kružnice
sú priesečníky kružnice  a priamky
a priamky 

3.2. Konštrukčné úlohy na parabolu
Príklad 1: Zostrojte parabolu, ak je dané jej ohnisko  a dva rôzne body
a dva rôzne body 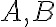 patriace tejto parabole. Riešenie príkladu v GeoGebre.
patriace tejto parabole. Riešenie príkladu v GeoGebre.
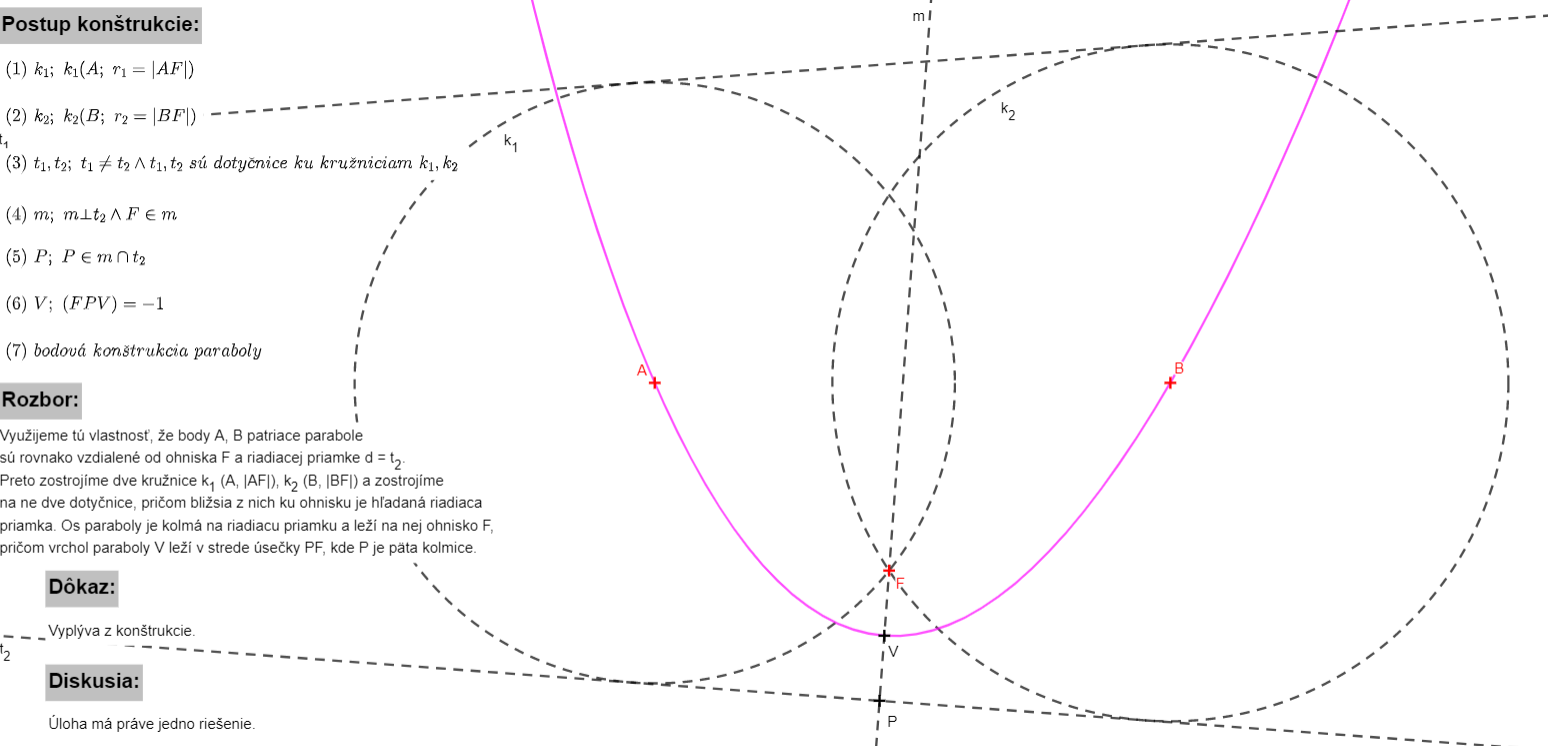
 a dva rôzne body
a dva rôzne body 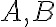 patriace tejto parabole. Riešenie príkladu v GeoGebre.
patriace tejto parabole. Riešenie príkladu v GeoGebre.
Príklad 2: Daná je priamka  a dva rôzne body
a dva rôzne body 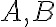 neležiace na priamke
neležiace na priamke  . Zostrojte parabolu, aby priamka
. Zostrojte parabolu, aby priamka  bola jej riadiaca priamka a body
bola jej riadiaca priamka a body 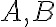 boli jej
body. Riešenie príkladu v GeoGebre.
boli jej
body. Riešenie príkladu v GeoGebre.
 a dva rôzne body
a dva rôzne body 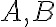 neležiace na priamke
neležiace na priamke  . Zostrojte parabolu, aby priamka
. Zostrojte parabolu, aby priamka  bola jej riadiaca priamka a body
bola jej riadiaca priamka a body 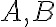 boli jej
body. Riešenie príkladu v GeoGebre.
boli jej
body. Riešenie príkladu v GeoGebre. 
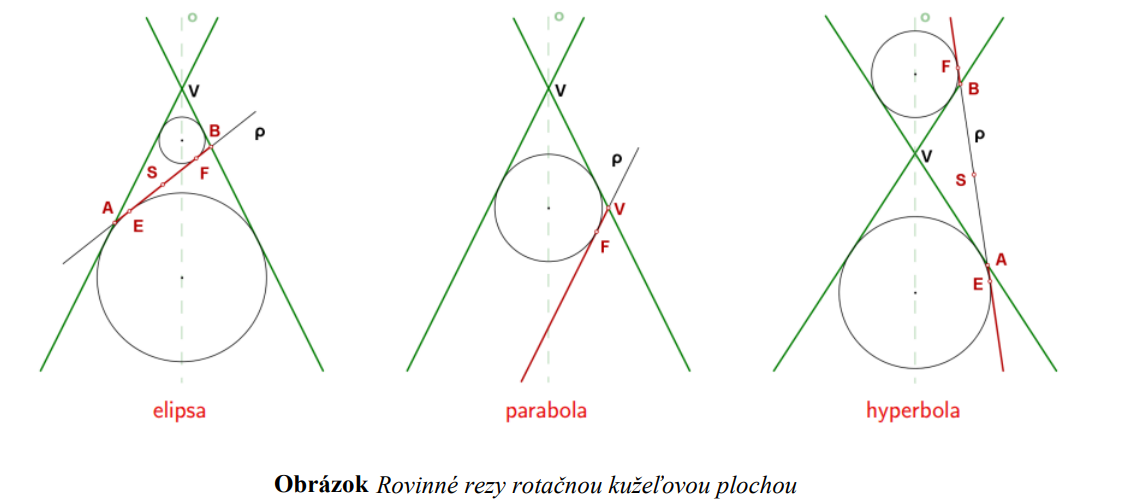
4. Kužeľosečka ako rovinný rez rotačnej kužeľovej plochy
Quételetova – Dandelinova veta:
Rezom rotačnou kužeľovou plochou neprechádzajúcou jej vrcholom, je:
• elipsa práve vtedy, keď rovinný rez pretína všetky tvoriace priamky kužeľovej plochy;
• parabola práve vtedy, keď rovinný rez je rovnobežný práve s jednou tvoriacou priamkou kužeľovej plochy;
• hyperbola práve vtedy, keď rovinný rez je rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
Tieto kužeľosečky majú ohniská v dotykových bodoch guľových plôch vpísaných rotačnej kužeľovej ploche a dotýkajúcich sa rovinných rezov.
Rezom rotačnou kužeľovou plochou neprechádzajúcou jej vrcholom, je:
• elipsa práve vtedy, keď rovinný rez pretína všetky tvoriace priamky kužeľovej plochy;
• parabola práve vtedy, keď rovinný rez je rovnobežný práve s jednou tvoriacou priamkou kužeľovej plochy;
• hyperbola práve vtedy, keď rovinný rez je rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
Tieto kužeľosečky majú ohniská v dotykových bodoch guľových plôch vpísaných rotačnej kužeľovej ploche a dotýkajúcich sa rovinných rezov.

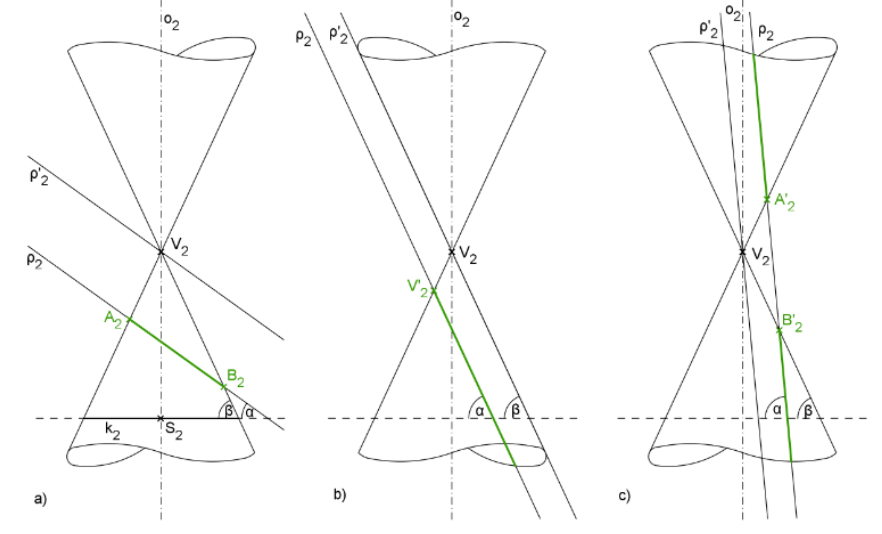
Nech  je rovinný rez neprechádzajúci vrcholom rotačnej kužeľovej plochy
je rovinný rez neprechádzajúci vrcholom rotačnej kužeľovej plochy  .
.
Nech je uhol, ktorý zvierajú tvoriace priamky rotačnej kužeľovej plochy s rovinou kolmou na os kužeľovej plochy.
je uhol, ktorý zvierajú tvoriace priamky rotačnej kužeľovej plochy s rovinou kolmou na os kužeľovej plochy.
Nech je uhol, ktorý zviera rovinný rez s rovinou kolmou na os kužeľovej plochy. Rezom
je uhol, ktorý zviera rovinný rez s rovinou kolmou na os kužeľovej plochy. Rezom  je:
je:
• elipsa práve vtedy, keď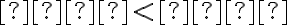 ;
;
• parabola práve vtedy, keď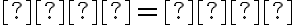 ;
;
• hyperbola práve vtedy, keď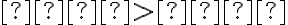 .
.
 je rovinný rez neprechádzajúci vrcholom rotačnej kužeľovej plochy
je rovinný rez neprechádzajúci vrcholom rotačnej kužeľovej plochy  .
.
Nech
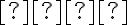 je uhol, ktorý zvierajú tvoriace priamky rotačnej kužeľovej plochy s rovinou kolmou na os kužeľovej plochy.
je uhol, ktorý zvierajú tvoriace priamky rotačnej kužeľovej plochy s rovinou kolmou na os kužeľovej plochy.
Nech
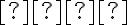 je uhol, ktorý zviera rovinný rez s rovinou kolmou na os kužeľovej plochy. Rezom
je uhol, ktorý zviera rovinný rez s rovinou kolmou na os kužeľovej plochy. Rezom 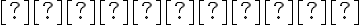 je:
je:
• elipsa práve vtedy, keď
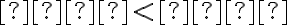 ;
;
• parabola práve vtedy, keď
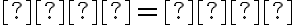 ;
;
• hyperbola práve vtedy, keď
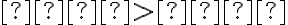 .
.

4.1. Dôkaz vety pre elipsu
Ak chceme dokázať, že prienik rovinného rezu  a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je elipsa,
je elipsa,
tak nám stačí ukázať, že body tohto prieniku majú konštantný súčet vzdialeností od dvoch pevných bodov (ohnísk).
Do rotačnej kužeľovej plochy vpíšeme dve guľové plochy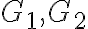
dotýkajúce sa tejto kužeľovej plochy pozdĺž kružníc
pozdĺž kružníc 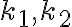 tak,
tak,
aby rovinný rez bol ich spoločná dotyková rovina s bodmi dotyku
bol ich spoločná dotyková rovina s bodmi dotyku  .
.
Zvoľme ľubovoľný bod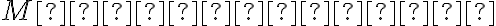 a ukážeme, že tento bod
a ukážeme, že tento bod  patrí elipse.
patrí elipse.
Ďalej nech priamka (povrchová cez kužeľovú plochu) je taká,
je taká,
že prechádza obomi kružnicami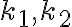 a zároveň
a zároveň 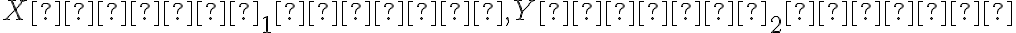 . Platí:
. Platí:
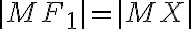 ,
,
pretože priamky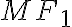 ,
, 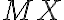 sú dotyčnice guľovej plochy
sú dotyčnice guľovej plochy 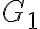 a zároveň body
a zároveň body 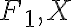 na tejto guľovej ploche ležia.
na tejto guľovej ploche ležia.
Obdobne platí:
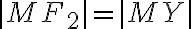 .
.
Pre vzdialenosť bodov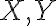 dostávame nasledujúcu rovnosť:
dostávame nasledujúcu rovnosť:
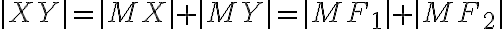 .
.
Takto sme dostali, že všetky také body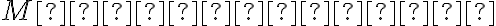 sú vzdialené od dvoch pevných bodov
sú vzdialené od dvoch pevných bodov  o konštantný súčet vzdialeností.
o konštantný súčet vzdialeností.
Takúto množinu bodov danej vlastnosti nazývame elipsa.
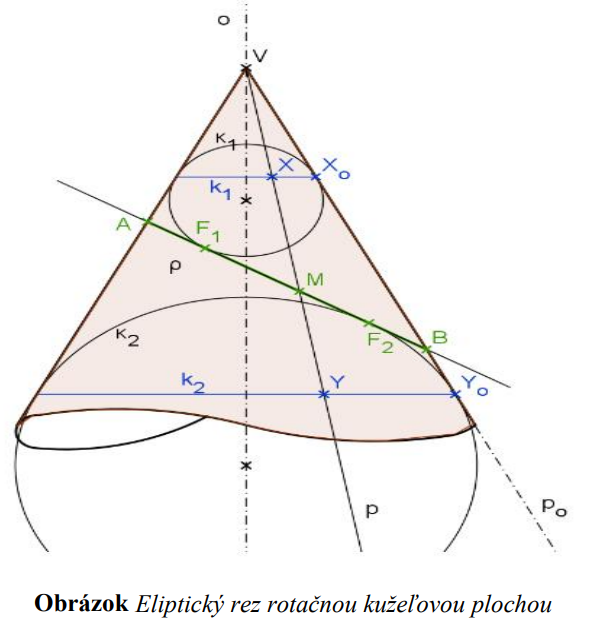
 a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je elipsa,
je elipsa,
tak nám stačí ukázať, že body tohto prieniku majú konštantný súčet vzdialeností od dvoch pevných bodov (ohnísk).
Do rotačnej kužeľovej plochy vpíšeme dve guľové plochy
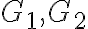
dotýkajúce sa tejto kužeľovej plochy
 pozdĺž kružníc
pozdĺž kružníc 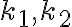 tak,
tak,
aby rovinný rez
 bol ich spoločná dotyková rovina s bodmi dotyku
bol ich spoločná dotyková rovina s bodmi dotyku  .
.
Zvoľme ľubovoľný bod
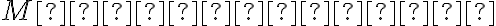 a ukážeme, že tento bod
a ukážeme, že tento bod  patrí elipse.
patrí elipse.
Ďalej nech priamka (povrchová cez kužeľovú plochu)
 je taká,
je taká,
že prechádza obomi kružnicami
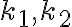 a zároveň
a zároveň 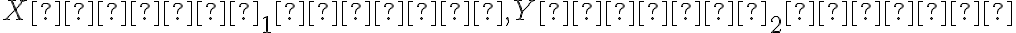 . Platí:
. Platí: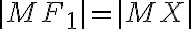 ,
,
pretože priamky
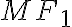 ,
, 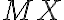 sú dotyčnice guľovej plochy
sú dotyčnice guľovej plochy 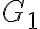 a zároveň body
a zároveň body 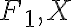 na tejto guľovej ploche ležia.
na tejto guľovej ploche ležia.
Obdobne platí:
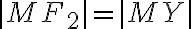 .
.
Pre vzdialenosť bodov
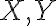 dostávame nasledujúcu rovnosť:
dostávame nasledujúcu rovnosť:
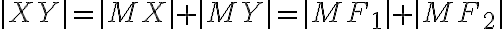 .
.
Takto sme dostali, že všetky také body
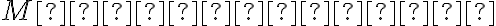 sú vzdialené od dvoch pevných bodov
sú vzdialené od dvoch pevných bodov  o konštantný súčet vzdialeností.
o konštantný súčet vzdialeností.
Takúto množinu bodov danej vlastnosti nazývame elipsa.

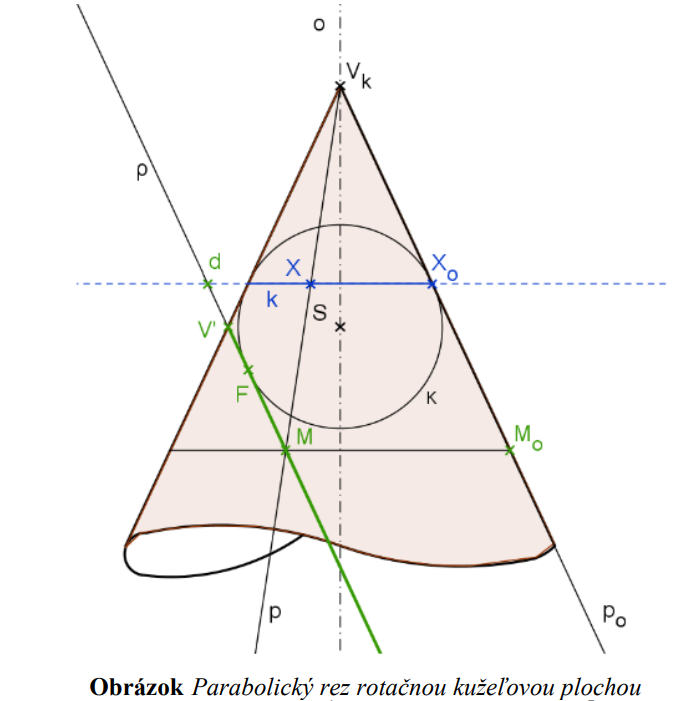
4.2. Dôkaz vety pre parabolu
Nech je daná rotačná kužeľová plocha  a rovinný rez
a rovinný rez  rovnobežný práve s jednou tvoriacou priamkou kužeľovej plochy.
rovnobežný práve s jednou tvoriacou priamkou kužeľovej plochy.
Ak chceme dokázať, že prienik rovinného rezu a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je parabola,
je parabola,
tak nám stačí ukázať, že body tohto prieniku majú konštantnú vzdialenosť od pevného bodu (ohnisko) a (riadiacej) priamky.
Do rotačnej kužeľovej plochy vpíšeme guľovú plochu
vpíšeme guľovú plochu 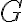 tak, aby rovinný rez
tak, aby rovinný rez  bola dotyková rovina tejto guľovej plochy.
bola dotyková rovina tejto guľovej plochy.
Bod dotyku označme . Guľová plocha
. Guľová plocha 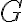 sa dotýka rotačnej kužeľovej plochy v podobe kružnice
sa dotýka rotačnej kužeľovej plochy v podobe kružnice  , pričom rovina, v ktorej leží kružnica, pretína rovinný rez
, pričom rovina, v ktorej leží kružnica, pretína rovinný rez  v priamke
v priamke  .
.
Ľubovoľným bodom rovinného rezu vedieme povrchovú priamku
vedieme povrchovú priamku  rotačnej kužeľovej plochy
rotačnej kužeľovej plochy  . Priamka
. Priamka  je dotyčnicou guľovej plochy
je dotyčnicou guľovej plochy 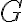 a dotýka sa v bode
a dotýka sa v bode 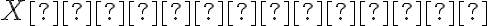 . Ďalšou dotyčnicou guľovej plochy
. Ďalšou dotyčnicou guľovej plochy  prechádzajúcou bodom
prechádzajúcou bodom  je priamka
je priamka 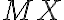 .
.
Keďže dĺžky dotyčníc z bodu ku guľovej ploche sú rovnaké, tak platí:
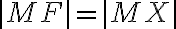 .
.
Dostali sme, že všetky body sú rovnako vzdialené od pevne zvoleného bodu
sú rovnako vzdialené od pevne zvoleného bodu  a priamky
a priamky  .
.
Takúto množinu bodov danej vlastnosti nazývame parabola.
 a rovinný rez
a rovinný rez  rovnobežný práve s jednou tvoriacou priamkou kužeľovej plochy.
rovnobežný práve s jednou tvoriacou priamkou kužeľovej plochy.
Ak chceme dokázať, že prienik rovinného rezu
 a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je parabola,
je parabola,
tak nám stačí ukázať, že body tohto prieniku majú konštantnú vzdialenosť od pevného bodu (ohnisko) a (riadiacej) priamky.
Do rotačnej kužeľovej plochy
 vpíšeme guľovú plochu
vpíšeme guľovú plochu  tak, aby rovinný rez
tak, aby rovinný rez  bola dotyková rovina tejto guľovej plochy.
bola dotyková rovina tejto guľovej plochy.
Bod dotyku označme
 . Guľová plocha
. Guľová plocha  sa dotýka rotačnej kužeľovej plochy v podobe kružnice
sa dotýka rotačnej kužeľovej plochy v podobe kružnice  , pričom rovina, v ktorej leží kružnica, pretína rovinný rez
, pričom rovina, v ktorej leží kružnica, pretína rovinný rez  v priamke
v priamke  .
.
Ľubovoľným bodom rovinného rezu
 vedieme povrchovú priamku
vedieme povrchovú priamku  rotačnej kužeľovej plochy
rotačnej kužeľovej plochy  . Priamka
. Priamka  je dotyčnicou guľovej plochy
je dotyčnicou guľovej plochy 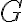 a dotýka sa v bode
a dotýka sa v bode 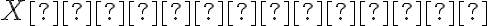 . Ďalšou dotyčnicou guľovej plochy
. Ďalšou dotyčnicou guľovej plochy 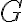 prechádzajúcou bodom
prechádzajúcou bodom  je priamka
je priamka 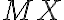 .
.
Keďže dĺžky dotyčníc z bodu ku guľovej ploche sú rovnaké, tak platí:
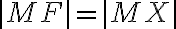 .
.
Dostali sme, že všetky body
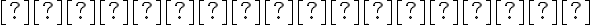 sú rovnako vzdialené od pevne zvoleného bodu
sú rovnako vzdialené od pevne zvoleného bodu  a priamky
a priamky  .
.
Takúto množinu bodov danej vlastnosti nazývame parabola.

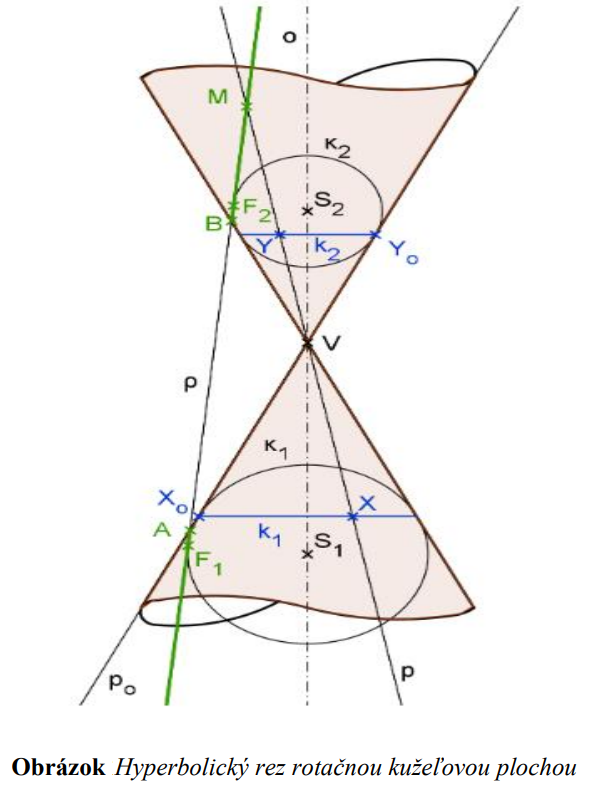
4.3. Dôkaz vety pre hyperbolu
Nech je daná rotačná kužeľová plocha  a rovinný rez
a rovinný rez  rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
Ak chceme dokázať, že prienik rovinného rezu a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je hyperbola, tak nám stačí ukázať,
je hyperbola, tak nám stačí ukázať,
že body tohto prieniku majú konštantný rozdiel vzdialeností od dvoch pevných bodov (ohniská).
(ohniská).
Do rotačnej kužeľovej plochy vpíšeme guľové plochy
vpíšeme guľové plochy 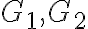 (dotýkajúce sa kužeľovej plochy pozdĺž kružníc
(dotýkajúce sa kužeľovej plochy pozdĺž kružníc 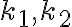 ) tak,
) tak,
aby rovinný rez bol ich dotyková rovina. Body dotyku označíme
bol ich dotyková rovina. Body dotyku označíme  .
.
Zvolíme si ľubovoľný bod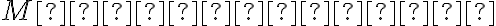 . Budeme viesť povrchovú priamku rotačnej kužeľovej plochy
. Budeme viesť povrchovú priamku rotačnej kužeľovej plochy  prechádzajúcu týmto bodom.
prechádzajúcu týmto bodom.
Označme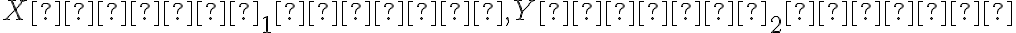 . Platí:
. Platí:
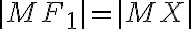 ,
,
pretože priamky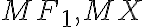 sú dotyčnice guľovej plochy
sú dotyčnice guľovej plochy 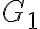 a zároveň body
a zároveň body 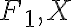 na tejto guľovej ploche ležia. Obdobne platí:
na tejto guľovej ploche ležia. Obdobne platí:
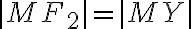 .
.
Dostávame, že:
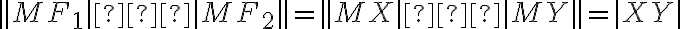 .
.
Takto sme dostali, že všetky také body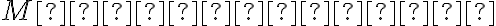 sú vzdialené od dvoch pevných bodov
sú vzdialené od dvoch pevných bodov  o konštantný rozdiel vzdialeností.
o konštantný rozdiel vzdialeností.
Takúto množinu bodov danej vlastnosti nazývame hyperbola.
 a rovinný rez
a rovinný rez  rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
rovnobežný práve s dvomi tvoriacimi priamkami kužeľovej plochy.
Ak chceme dokázať, že prienik rovinného rezu
 a rotačnej kužeľovej plochy
a rotačnej kužeľovej plochy  je hyperbola, tak nám stačí ukázať,
je hyperbola, tak nám stačí ukázať,
že body tohto prieniku majú konštantný rozdiel vzdialeností od dvoch pevných bodov
 (ohniská).
(ohniská).
Do rotačnej kužeľovej plochy
 vpíšeme guľové plochy
vpíšeme guľové plochy 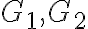 (dotýkajúce sa kužeľovej plochy pozdĺž kružníc
(dotýkajúce sa kužeľovej plochy pozdĺž kružníc 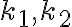 ) tak,
) tak,
aby rovinný rez
 bol ich dotyková rovina. Body dotyku označíme
bol ich dotyková rovina. Body dotyku označíme  .
.
Zvolíme si ľubovoľný bod
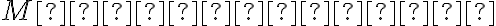 . Budeme viesť povrchovú priamku rotačnej kužeľovej plochy
. Budeme viesť povrchovú priamku rotačnej kužeľovej plochy  prechádzajúcu týmto bodom.
prechádzajúcu týmto bodom.
Označme
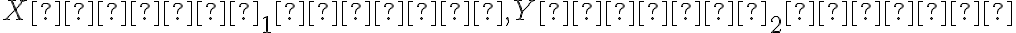 . Platí:
. Platí:
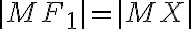 ,
,
pretože priamky
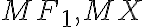 sú dotyčnice guľovej plochy
sú dotyčnice guľovej plochy 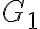 a zároveň body
a zároveň body 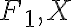 na tejto guľovej ploche ležia. Obdobne platí:
na tejto guľovej ploche ležia. Obdobne platí:
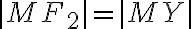 .
.
Dostávame, že:
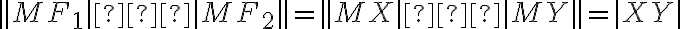 .
.
Takto sme dostali, že všetky také body
 sú vzdialené od dvoch pevných bodov
sú vzdialené od dvoch pevných bodov  o konštantný rozdiel vzdialeností.
o konštantný rozdiel vzdialeností.
Takúto množinu bodov danej vlastnosti nazývame hyperbola.

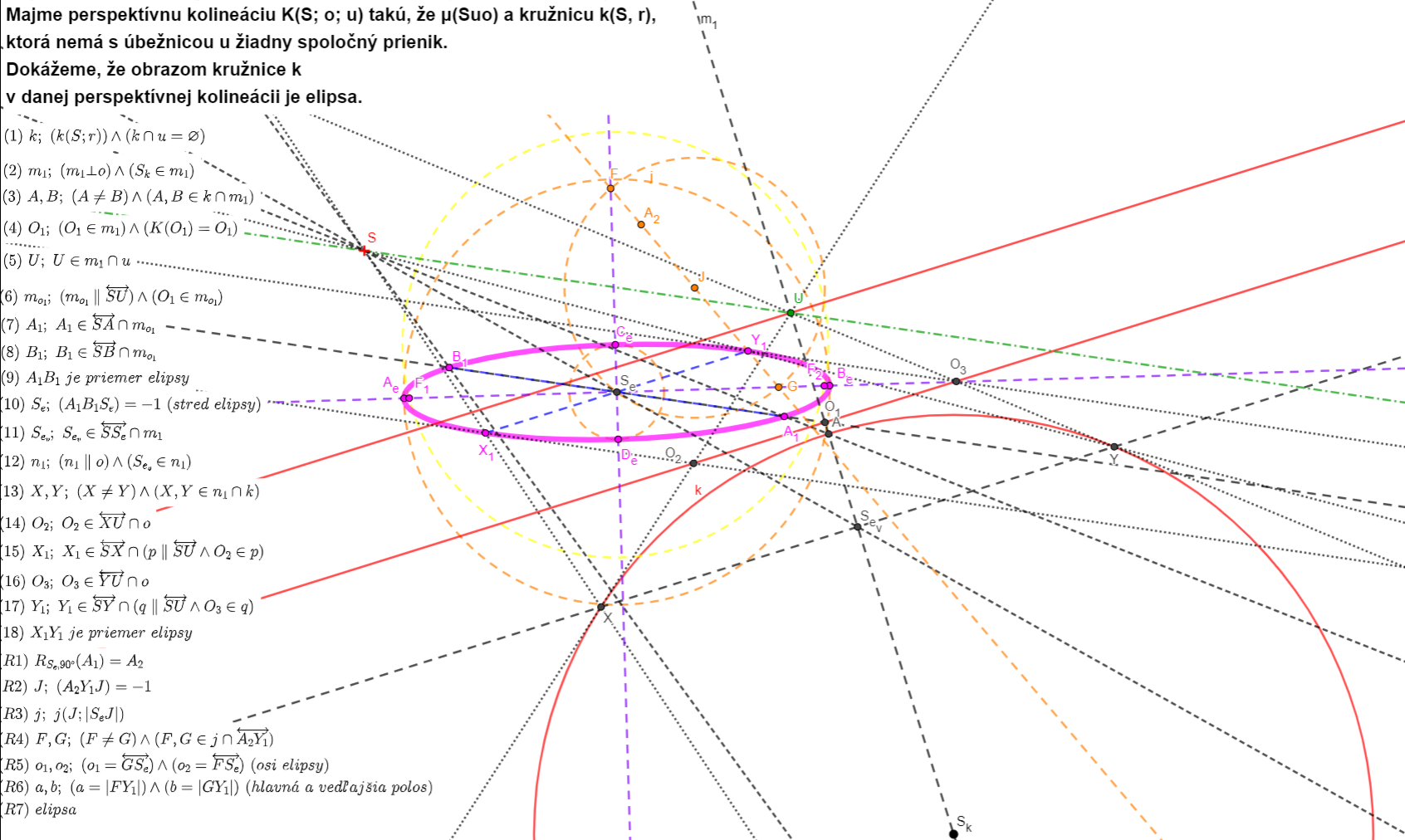
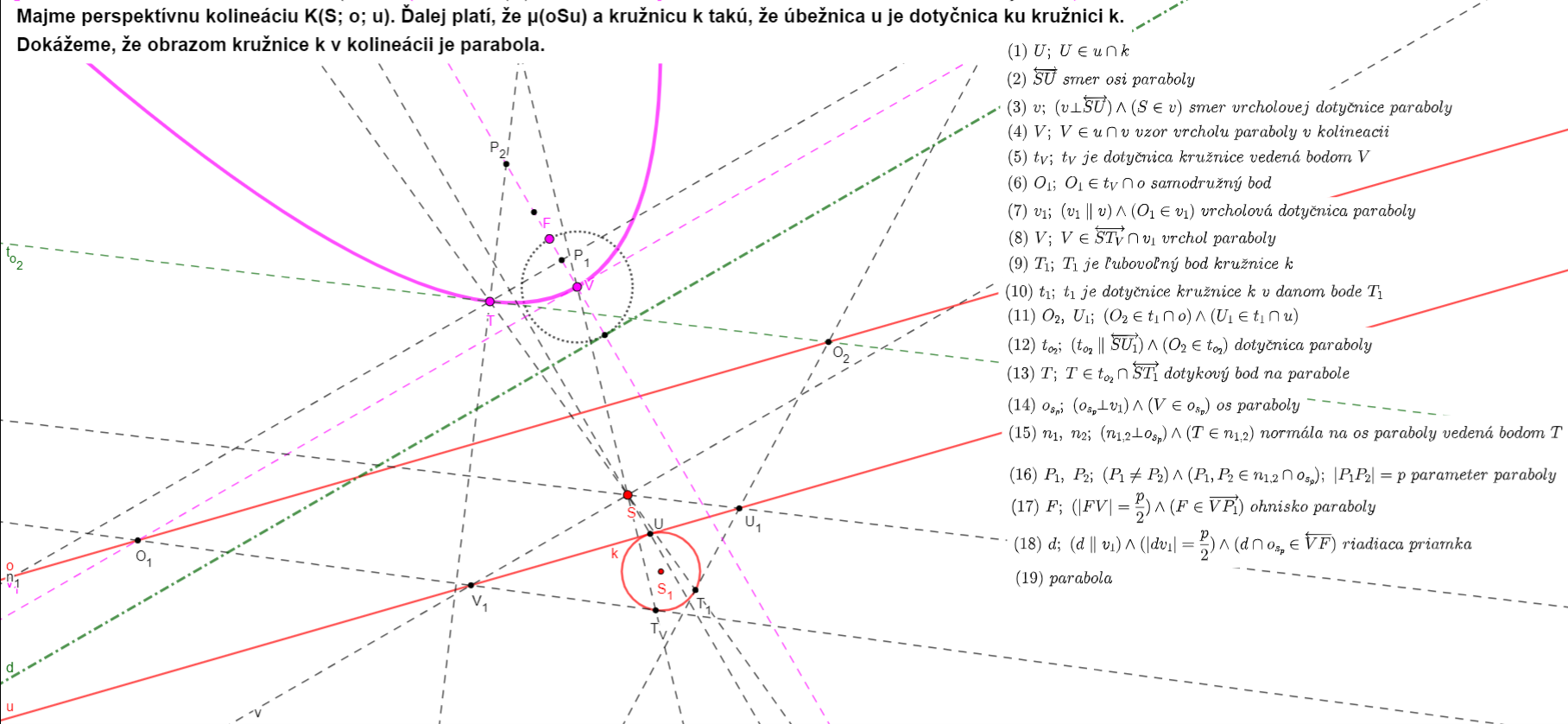
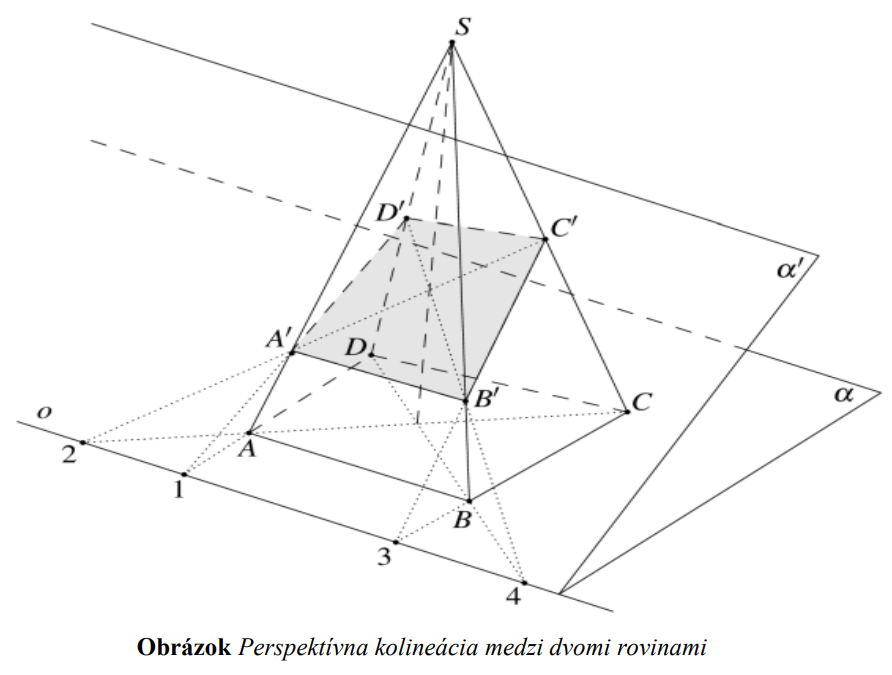
5. Kužeľosečka ako obraz kružnice v perspektívnej kolineácii
Nech 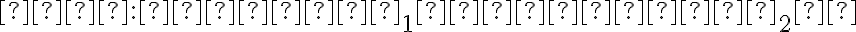 je perspektívna kolineácia daná stredom
je perspektívna kolineácia daná stredom  , osou perspektívnej kolineácie
, osou perspektívnej kolineácie  a úbežnicou
a úbežnicou 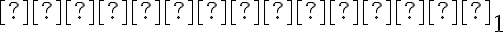 .
.
Potom obrazom kružnice v
v  je:
je:
• elipsa práve vtedy, keď úbežnica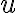 je nesečnica kružnice
je nesečnica kružnice 
• parabola práve vtedy, keď úbežnica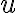 je dotyčnica kružnice
je dotyčnica kružnice 
• hyperbola práve vtedy, keď úbežnica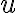 je sečnica kružnice
je sečnica kružnice  .
.
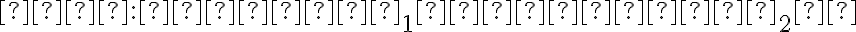 je perspektívna kolineácia daná stredom
je perspektívna kolineácia daná stredom  , osou perspektívnej kolineácie
, osou perspektívnej kolineácie  a úbežnicou
a úbežnicou 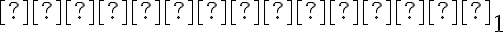 .
.
Potom obrazom kružnice
 v
v 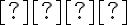 je:
je:
• elipsa práve vtedy, keď úbežnica
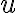 je nesečnica kružnice
je nesečnica kružnice 
• parabola práve vtedy, keď úbežnica
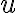 je dotyčnica kružnice
je dotyčnica kružnice 
• hyperbola práve vtedy, keď úbežnica
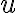 je sečnica kružnice
je sečnica kružnice  .
.Majme danú priamku 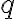 a bod
a bod 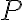 , ktorý na tejto priamke neleží. Zostrojme priamku
, ktorý na tejto priamke neleží. Zostrojme priamku  tak, aby prechádzala bodom
tak, aby prechádzala bodom 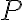 .
.
Postupne budeme otáčať priamku okolo bodu
okolo bodu 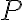 a dostávame priesečníky s priamkou
a dostávame priesečníky s priamkou 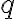 . V určitom okamihu priamky
. V určitom okamihu priamky 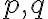 budú
navzájom rôzne rovnobežné a už nedostaneme ich priesečník.
budú
navzájom rôzne rovnobežné a už nedostaneme ich priesečník.
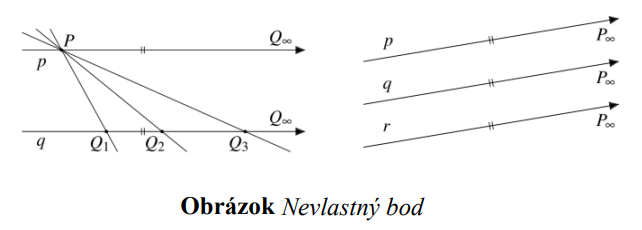
Túto situáciu neexistujúceho priesečníku rôzne rovnobežných priamok vyriešime tak, že zavedieme nevlastný bod ako priesečník rôzne rovnobežných priamok v nekonečne.
Nevlastné body označujeme dolným indexom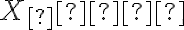 . Ďalej platí, že všetky navzájom rôzne rovnobežné priamky
. Ďalej platí, že všetky navzájom rôzne rovnobežné priamky
so spoločným smerom majú spoločný práve jeden nevlastný bod. Každá priamka má práve jeden nevlastný bod.
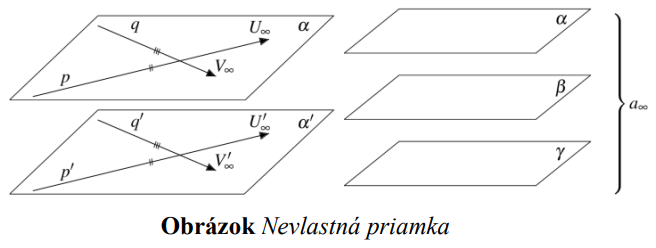
Obdobne vieme pre rôzne rovnobežné roviny zaviesť nevlastnú priamku ako priesečník rôznych rovnobežných rovín,
pričom nevlastná priama je daná dvomi smermi (tzv. zameraním roviny). Každá rovina má práve jednu nevlastnú priamku
Nevlastná rovina je množina všetkých nevlastných bodov a nevlastných priamok rozšíreného Euklidovského priestoru.
Každý priestor má práve jednu nevlastnú rovinu.
.
 a bod
a bod  , ktorý na tejto priamke neleží. Zostrojme priamku
, ktorý na tejto priamke neleží. Zostrojme priamku  tak, aby prechádzala bodom
tak, aby prechádzala bodom 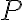 .
.
Postupne budeme otáčať priamku
 okolo bodu
okolo bodu 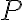 a dostávame priesečníky s priamkou
a dostávame priesečníky s priamkou 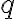 . V určitom okamihu priamky
. V určitom okamihu priamky 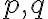 budú
navzájom rôzne rovnobežné a už nedostaneme ich priesečník.
budú
navzájom rôzne rovnobežné a už nedostaneme ich priesečník.
Túto situáciu neexistujúceho priesečníku rôzne rovnobežných priamok vyriešime tak, že zavedieme nevlastný bod ako priesečník rôzne rovnobežných priamok v nekonečne.
Nevlastné body označujeme dolným indexom
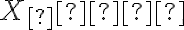 . Ďalej platí, že všetky navzájom rôzne rovnobežné priamky
. Ďalej platí, že všetky navzájom rôzne rovnobežné priamky
so spoločným smerom majú spoločný práve jeden nevlastný bod. Každá priamka má práve jeden nevlastný bod.

Obdobne vieme pre rôzne rovnobežné roviny zaviesť nevlastnú priamku ako priesečník rôznych rovnobežných rovín,
pričom nevlastná priama je daná dvomi smermi (tzv. zameraním roviny). Každá rovina má práve jednu nevlastnú priamku
Nevlastná rovina je množina všetkých nevlastných bodov a nevlastných priamok rozšíreného Euklidovského priestoru.
Každý priestor má práve jednu nevlastnú rovinu.
.

Nech sú dané dve rôzne roviny 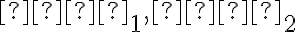 a bod
a bod  , ktorý neleží ani na jednej z daných rovín.
, ktorý neleží ani na jednej z daných rovín.
Perspektívna kolineácia 𝓚 je bijektívne zobrazenie dvoch rovín, pri ktorom každému bodu prvej roviny odpovedá jeho priemet zo stredu do roviny druhej.
do roviny druhej.
Bod nazývame stred kolineácie, priamku
nazývame stred kolineácie, priamku 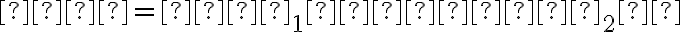 nazývame osou perspektívnej
kolineácie.
nazývame osou perspektívnej
kolineácie.
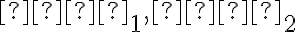 a bod
a bod  , ktorý neleží ani na jednej z daných rovín.
, ktorý neleží ani na jednej z daných rovín.
Perspektívna kolineácia 𝓚 je bijektívne zobrazenie dvoch rovín, pri ktorom každému bodu prvej roviny odpovedá jeho priemet zo stredu
 do roviny druhej.
do roviny druhej.
Bod
 nazývame stred kolineácie, priamku
nazývame stred kolineácie, priamku 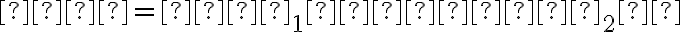 nazývame osou perspektívnej
kolineácie.
nazývame osou perspektívnej
kolineácie.

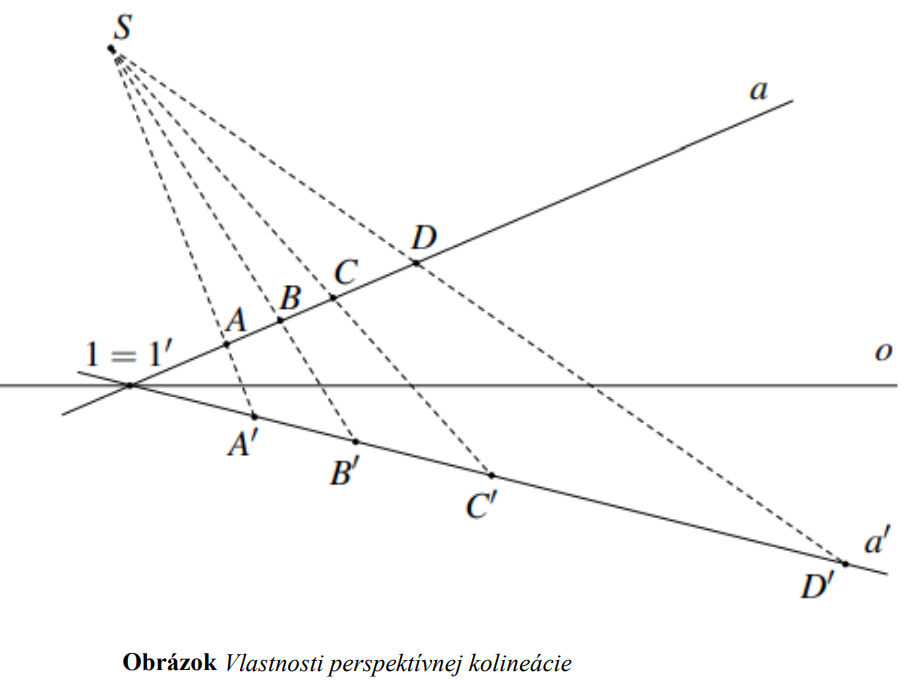
Medzi základné vlastnosti perspektívnej kolineácie medzi dvomi rovinami, vyplývajúce z toho, že ide o bijektívne zobrazenie, zaraďujeme:
• bod sa zobrazí na bod, priamka sa zobrazí na priamku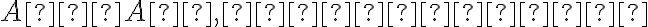
• kolineárne združené body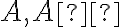 , ktoré si odpovedajú v kolineácii, ležia na priamke prechádzajúce stredom kolineácie
, ktoré si odpovedajú v kolineácii, ležia na priamke prechádzajúce stredom kolineácie 
• vlastnému bodu môže odpovedať nevlastný bod alebo naopak
• priamky odpovedajúce si v kolineácii sa pretínajú na osi perspektívnej kolineácii ,
,
pričom priesečníky týchto priamok sú samodružné body
• zachováva sa incidencia, takže ak jeden útvar patrí druhému útvaru, tak aj ich obrazy si zachovávajú tú istú vlastnosť
• nezachováva sa deliaci pomer troch bodov na priamke, z toho vyplýva, že ani rovnobežnosť nie je invariantom kolineácie
• deliaci dvojpomer štyroch bodov na priamke je invariantom kolineácie.
• bod sa zobrazí na bod, priamka sa zobrazí na priamku
• kolineárne združené body
 , ktoré si odpovedajú v kolineácii, ležia na priamke prechádzajúce stredom kolineácie
, ktoré si odpovedajú v kolineácii, ležia na priamke prechádzajúce stredom kolineácie 
• vlastnému bodu môže odpovedať nevlastný bod alebo naopak
• priamky odpovedajúce si v kolineácii sa pretínajú na osi perspektívnej kolineácii
 ,
,
pričom priesečníky týchto priamok sú samodružné body
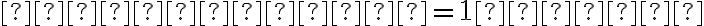
• zachováva sa incidencia, takže ak jeden útvar patrí druhému útvaru, tak aj ich obrazy si zachovávajú tú istú vlastnosť
• nezachováva sa deliaci pomer troch bodov na priamke, z toho vyplýva, že ani rovnobežnosť nie je invariantom kolineácie
• deliaci dvojpomer štyroch bodov na priamke je invariantom kolineácie.

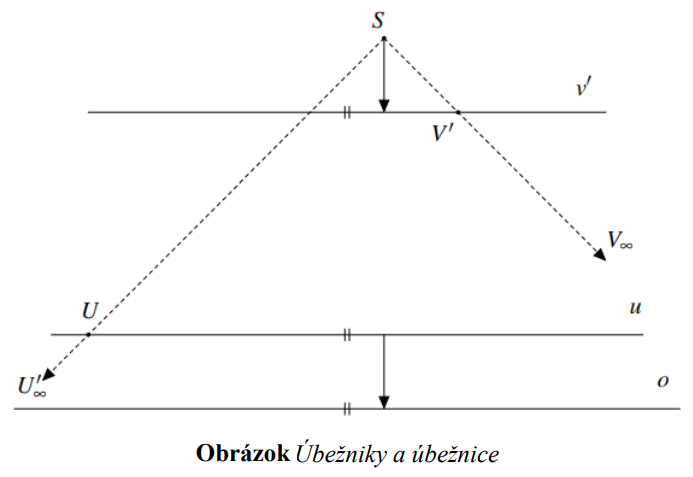
Body, ktoré sú v perspektívnej kolineácii obrazy alebo vzory nevlastných bodov, nazývame úbežníky.
Priamky, ktoré sú v perspektívnej kolineácii obrazom alebo vzorom nevlastnej priamky, nazývame úbežnice.
V perspektívnej kolineácii sú úbežnice dve. Úbežnica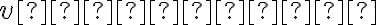 je obrazom nevlastnej priamky
je obrazom nevlastnej priamky 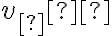 roviny
roviny 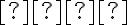 ,
,
úbežnica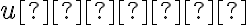 je vzor nevlastnej priamky
je vzor nevlastnej priamky 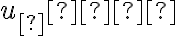 roviny
roviny 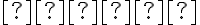 .
.
Ďalej platí, že úbežnice sú rovnobežné s osou perspektívnej kolineácie a všetky úbežníky ležia na
úbežniciach.
a všetky úbežníky ležia na
úbežniciach.
Obrazy rovnobežných priamok sa pretínajú na úbežnici. Orientovaná vzdialenosť stredu kolineácie
od jednej úbežnice sa rovná súhlasne orientovanej vzdialenosti druhej úbežnice od osi perspektívnej kolineácie .
.
Priamky, ktoré sú v perspektívnej kolineácii obrazom alebo vzorom nevlastnej priamky, nazývame úbežnice.
V perspektívnej kolineácii sú úbežnice dve. Úbežnica
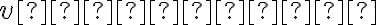 je obrazom nevlastnej priamky
je obrazom nevlastnej priamky 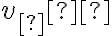 roviny
roviny  ,
,
úbežnica
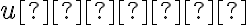 je vzor nevlastnej priamky
je vzor nevlastnej priamky 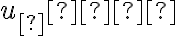 roviny
roviny 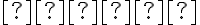 .
.
Ďalej platí, že úbežnice sú rovnobežné s osou perspektívnej kolineácie
 a všetky úbežníky ležia na
úbežniciach.
a všetky úbežníky ležia na
úbežniciach.
Obrazy rovnobežných priamok sa pretínajú na úbežnici. Orientovaná vzdialenosť stredu kolineácie

od jednej úbežnice sa rovná súhlasne orientovanej vzdialenosti druhej úbežnice od osi perspektívnej kolineácie
 .
.

5.1. Geometrický dôkaz vety pre elipsu
5.2. Geometrický dôkaz vety pre parabolu
5.3. Geometrický dôkaz vety pre hyperbolu
6. Analytické vyjadrenie kužeľosečiek
Kužeľosečka je množina bodov X[x; y] v rovine, ktoré vyhovujú nasledovnej rovnici lineárnej sústave súradníc:
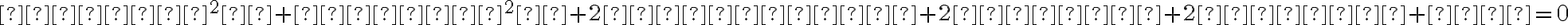 ,
,
pričom koeficienty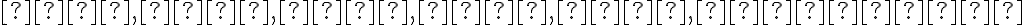 a jeden z koeficientov
a jeden z koeficientov 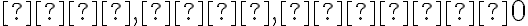 .
.
Túto rovnicu nazývame všeobecná rovnica kužeľosečiek.
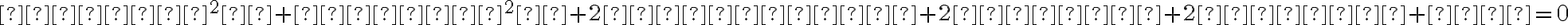 ,
,
pričom koeficienty
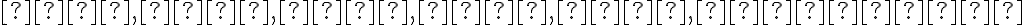 a jeden z koeficientov
a jeden z koeficientov 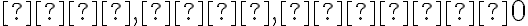 .
.
Túto rovnicu nazývame všeobecná rovnica kužeľosečiek.
Pod regulárnou kužeľosečkou rozumieme kružnicu, elipsu, hyperbolu a parabolu.
Pod singulárnou kužeľosečkou rozumieme každú dvojicu priamok (dve rôznobežné priamky, dve rôzne rovnobežné priamky) a bod.
Pod singulárnou kužeľosečkou rozumieme každú dvojicu priamok (dve rôznobežné priamky, dve rôzne rovnobežné priamky) a bod.
Všeobecnú rovnicu kužeľosečky vieme vyjadriť aj v maticovom tvare:
![\left[\begin{array}{ccc} x&y&1 \end{array}\right] \left[\begin{array}{ccc} x&y&1 \end{array}\right]](https://lms.umb.sk/filter/tex/pix.php/607490d7094c94725c35ed896d079e91.png)
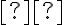
![\left[\begin{array}{ccc} x&y&1 \end{array}\right]^T \left[\begin{array}{ccc} x&y&1 \end{array}\right]^T](https://lms.umb.sk/filter/tex/pix.php/f9af86befe2d2125f2fc3013c9006d65.png) = 0,
= 0,
kde matica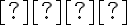 pozostáva z koeficientov všeobecnej rovnice a nazýva sa veľký diskriminant kužeľosečky:
pozostáva z koeficientov všeobecnej rovnice a nazýva sa veľký diskriminant kužeľosečky:
![σ = \left[\begin{array}{ccc} A&B&D \\ B&C&E \\ D&E&F\end{array}\right] σ = \left[\begin{array}{ccc} A&B&D \\ B&C&E \\ D&E&F\end{array}\right]](https://lms.umb.sk/filter/tex/pix.php/216defbb1f894f269e9362f88bd114cf.png) .
.
Malý diskriminant kužeľosečky má tvar:
![δ = \left[\begin{array}{cc} A&B\\ B&C\end{array}\right] δ = \left[\begin{array}{cc} A&B\\ B&C\end{array}\right]](https://lms.umb.sk/filter/tex/pix.php/034c74bac594332f63c514fb8d3869d1.png) .
.
![\left[\begin{array}{ccc} x&y&1 \end{array}\right] \left[\begin{array}{ccc} x&y&1 \end{array}\right]](https://lms.umb.sk/filter/tex/pix.php/607490d7094c94725c35ed896d079e91.png)
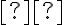
![\left[\begin{array}{ccc} x&y&1 \end{array}\right]^T \left[\begin{array}{ccc} x&y&1 \end{array}\right]^T](https://lms.umb.sk/filter/tex/pix.php/f9af86befe2d2125f2fc3013c9006d65.png) = 0,
= 0, kde matica
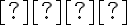 pozostáva z koeficientov všeobecnej rovnice a nazýva sa veľký diskriminant kužeľosečky:
pozostáva z koeficientov všeobecnej rovnice a nazýva sa veľký diskriminant kužeľosečky:
![σ = \left[\begin{array}{ccc} A&B&D \\ B&C&E \\ D&E&F\end{array}\right] σ = \left[\begin{array}{ccc} A&B&D \\ B&C&E \\ D&E&F\end{array}\right]](https://lms.umb.sk/filter/tex/pix.php/216defbb1f894f269e9362f88bd114cf.png) .
.
Malý diskriminant kužeľosečky má tvar:
![δ = \left[\begin{array}{cc} A&B\\ B&C\end{array}\right] δ = \left[\begin{array}{cc} A&B\\ B&C\end{array}\right]](https://lms.umb.sk/filter/tex/pix.php/034c74bac594332f63c514fb8d3869d1.png) .
.Na určenie konkrétneho druhu kužeľosečky pomocou veľkého a malého diskriminantu
všeobecnej rovnice kužeľosečiek sme zostavili kvôli priehľadnosti nasledujúci algoritmus:
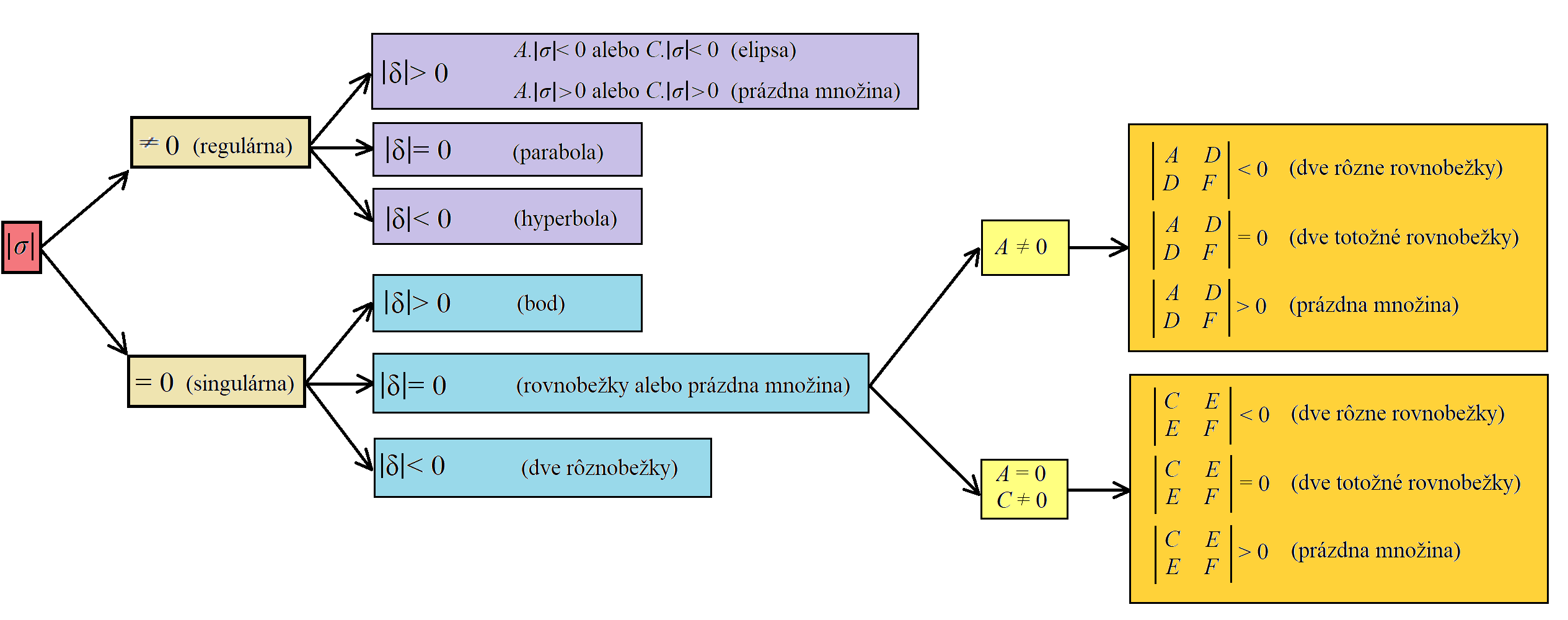
všeobecnej rovnice kužeľosečiek sme zostavili kvôli priehľadnosti nasledujúci algoritmus:

6.1. Stredová a vrcholová rovnica kužeľosečky
Elipsa  je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých súčet vzdialeností od dvoch pevných bodov (ohnísk) je stály a rovný
je stály a rovný  , pričom konštanta
, pričom konštanta  :
:
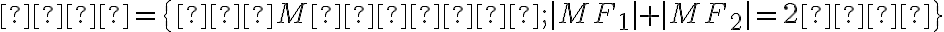 .
.
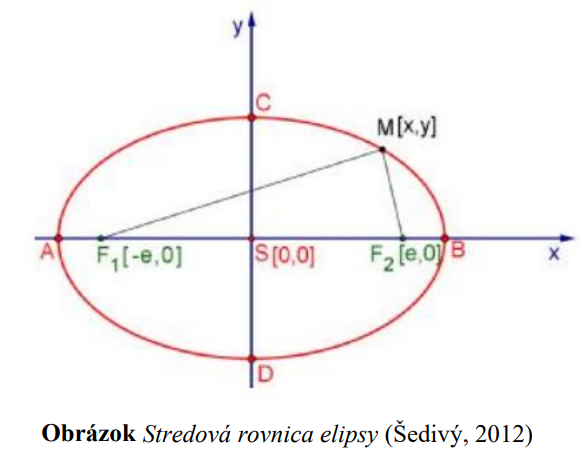
Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom elipsy, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme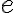 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod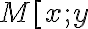 ] na elipse
] na elipse 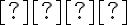 práve vtedy, keď platí:
práve vtedy, keď platí:
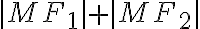 =
=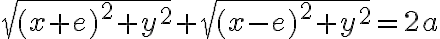 .
.
Ďalším umocňovaním a úpravami dostaneme:
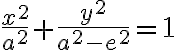 .
.
Ak stred elipsy je bod![S[m; n] S[m; n]](https://lms.umb.sk/filter/tex/pix.php/5052e1eedc1daed03437c681e8aa3d8e.png) a ohniská ležia na rovnobežke s osou
a ohniská ležia na rovnobežke s osou 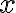 prechádzajúcou bodom
prechádzajúcou bodom  , potom stredová rovnica elipsy:
, potom stredová rovnica elipsy:
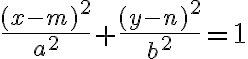 .
.
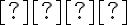 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých súčet vzdialeností od dvoch pevných bodov (ohnísk)
 je stály a rovný
je stály a rovný 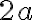 , pričom konštanta
, pričom konštanta 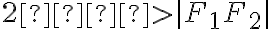 :
:
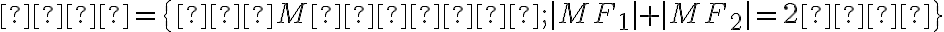 .
.

Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom elipsy, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme
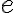 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod
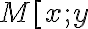 ] na elipse
] na elipse  práve vtedy, keď platí:
práve vtedy, keď platí:
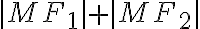 =
=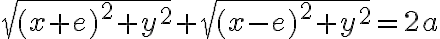 .
.
Ďalším umocňovaním a úpravami dostaneme:
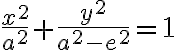 .
.
Ak stred elipsy je bod
![S[m; n] S[m; n]](https://lms.umb.sk/filter/tex/pix.php/5052e1eedc1daed03437c681e8aa3d8e.png) a ohniská ležia na rovnobežke s osou
a ohniská ležia na rovnobežke s osou 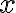 prechádzajúcou bodom
prechádzajúcou bodom  , potom stredová rovnica elipsy:
, potom stredová rovnica elipsy:
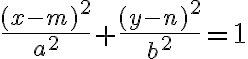 .
.
Hyperbola 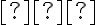 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
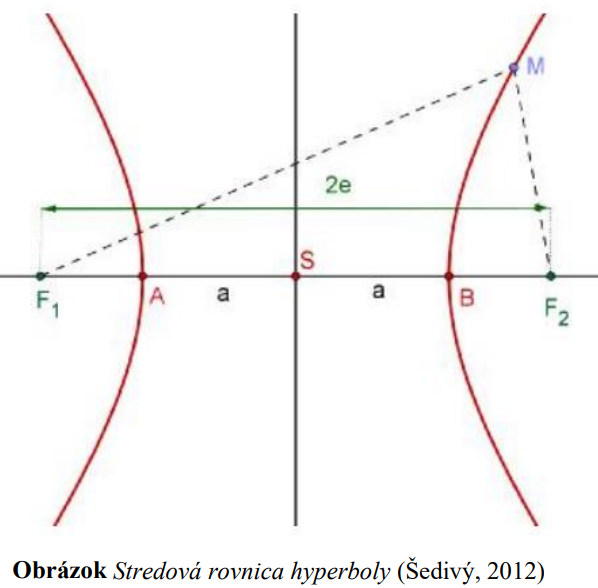
ktorých rozdiel vzdialeností od dvoch pevných bodov (ohnísk) je stály a rovný
je stály a rovný 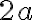 , pričom konštanta
, pričom konštanta 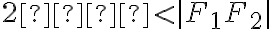 :
:
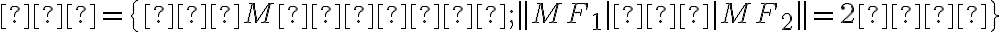 .
.
Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom hyperboly, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme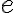 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/05b89453b51c3ac375aeacbc6a7f181d.png) na hyperbole
na hyperbole 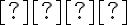 práve vtedy, keď platí:
práve vtedy, keď platí:
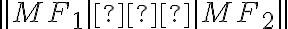 =|
=|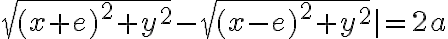 .
.
Ďalším umocňovaním a úpravami dostaneme:
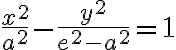 .
.
Ak stred hyperboly je bod S[m; n] a ohniská ležia na rovnobežke s osou x prechádzajúcou bodom S, potom stredová rovnica hyperboly:
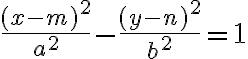 .
.
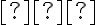 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých rozdiel vzdialeností od dvoch pevných bodov (ohnísk)
 je stály a rovný
je stály a rovný 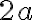 , pričom konštanta
, pričom konštanta 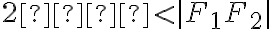 :
:
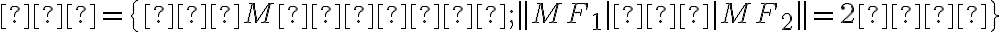 .
.

Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom hyperboly, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme
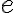 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod
![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/05b89453b51c3ac375aeacbc6a7f181d.png) na hyperbole
na hyperbole 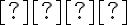 práve vtedy, keď platí:
práve vtedy, keď platí:
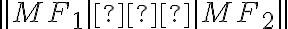 =|
=|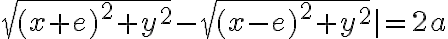 .
.
Ďalším umocňovaním a úpravami dostaneme:
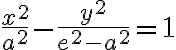 .
.
Ak stred hyperboly je bod S[m; n] a ohniská ležia na rovnobežke s osou x prechádzajúcou bodom S, potom stredová rovnica hyperboly:
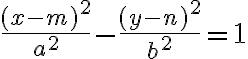 .
.
Parabola 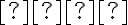 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktoré majú rovnakú vzdialenosť od pevného bodu (ohnisko) a pevnej (riadiacej) priamky
a pevnej (riadiacej) priamky  :
:
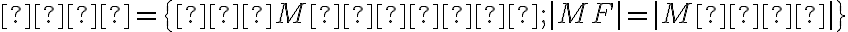 .
.
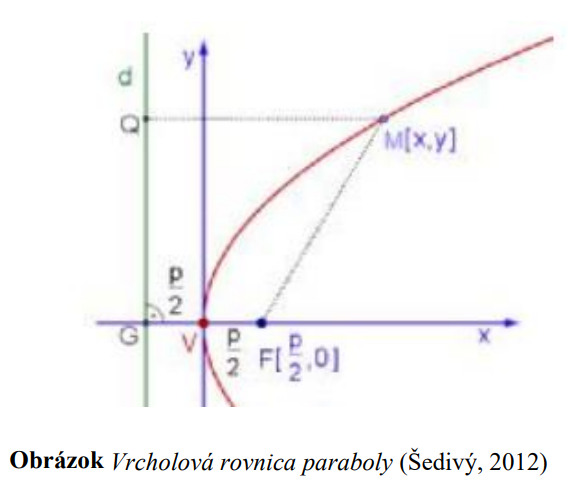
Parabolu v KSS umiestnime tak, aby vrchol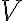 ležal na jej počiatku. Riadiacu priamku paraboly
ležal na jej počiatku. Riadiacu priamku paraboly  vieme popísať rovnicou
vieme popísať rovnicou
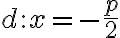 .
.
Ohnisko má súradnice![F[𝑝/2; 0] F[𝑝/2; 0]](https://lms.umb.sk/filter/tex/pix.php/a71f3cee78cfc5827342208f2a3b5e07.png) . Podľa definície leží bod
. Podľa definície leží bod ![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/cf2a1516111d0aba727db8b6611dc143.png) na parabole
na parabole 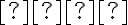 práve vtedy, keď platí:
práve vtedy, keď platí:
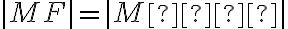 .
.
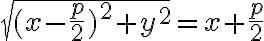 .
.
Ďalším umocňovaním a úpravami dostaneme:
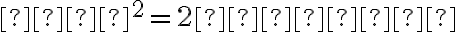 .
.
Ak vrchol paraboly je bod![V[m; n] V[m; n]](https://lms.umb.sk/filter/tex/pix.php/5088170b081e7fea2f4e42bface36dc0.png) a ohnisko leží na rovnobežke s osou
a ohnisko leží na rovnobežke s osou 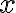 prechádzajúcou bodom
prechádzajúcou bodom 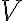 , potom vrcholová rovnica paraboly:
, potom vrcholová rovnica paraboly:
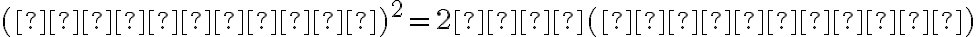 .
.
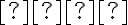 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktoré majú rovnakú vzdialenosť od pevného bodu (ohnisko)
 a pevnej (riadiacej) priamky
a pevnej (riadiacej) priamky  :
:
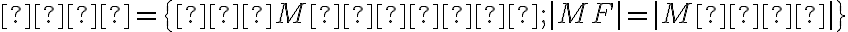 .
.

Parabolu v KSS umiestnime tak, aby vrchol
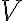 ležal na jej počiatku. Riadiacu priamku paraboly
ležal na jej počiatku. Riadiacu priamku paraboly  vieme popísať rovnicou
vieme popísať rovnicou
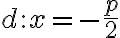 .
.
Ohnisko má súradnice
![F[𝑝/2; 0] F[𝑝/2; 0]](https://lms.umb.sk/filter/tex/pix.php/a71f3cee78cfc5827342208f2a3b5e07.png) . Podľa definície leží bod
. Podľa definície leží bod ![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/cf2a1516111d0aba727db8b6611dc143.png) na parabole
na parabole 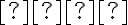 práve vtedy, keď platí:
práve vtedy, keď platí:
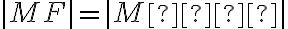 .
.
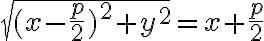 .
.
Ďalším umocňovaním a úpravami dostaneme:
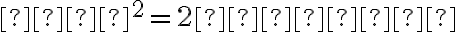 .
.
Ak vrchol paraboly je bod
![V[m; n] V[m; n]](https://lms.umb.sk/filter/tex/pix.php/5088170b081e7fea2f4e42bface36dc0.png) a ohnisko leží na rovnobežke s osou
a ohnisko leží na rovnobežke s osou 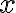 prechádzajúcou bodom
prechádzajúcou bodom 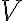 , potom vrcholová rovnica paraboly:
, potom vrcholová rovnica paraboly:
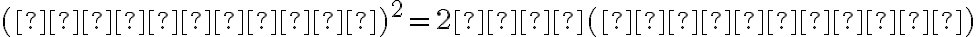 .
.
6.2. Transformácia karteziánskej sústavy súradníc
Nech karteziánska sústava súradníc je daná repérom 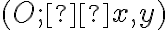 . Hovoríme, že nová sústava
. Hovoríme, že nová sústava 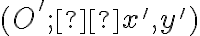 vznikla z pôvodnej sústavy
vznikla z pôvodnej sústavy 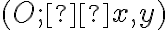
posunutím, ak platí medzi pôvodnými súradnicami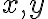 a novými súradnicami
a novými súradnicami 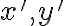 ľubovoľného bodu
ľubovoľného bodu  vzťah daný rovnicami:
vzťah daný rovnicami:
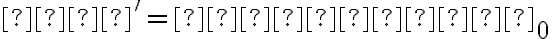
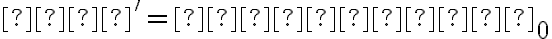
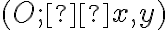 . Hovoríme, že nová sústava
. Hovoríme, že nová sústava 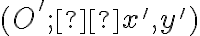 vznikla z pôvodnej sústavy
vznikla z pôvodnej sústavy 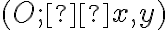
posunutím, ak platí medzi pôvodnými súradnicami
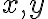 a novými súradnicami
a novými súradnicami 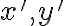 ľubovoľného bodu
ľubovoľného bodu  vzťah daný rovnicami:
vzťah daný rovnicami:
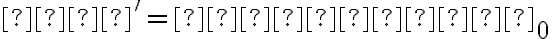
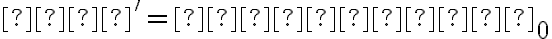
Nech karteziánska sústava súradníc je daná repérom 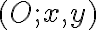 . Hovoríme, že nová sústava
. Hovoríme, že nová sústava 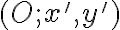 vznikla z pôvodnej sústavy
vznikla z pôvodnej sústavy 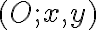
otočením okolo počiatku pôvodnej sústavy daným uhlom
daným uhlom 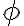 , ak platí medzi pôvodnými súradnicami
, ak platí medzi pôvodnými súradnicami 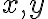
a novými súradnicami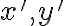 ľubovoľného bodu
ľubovoľného bodu  vzťah daný rovnicami:
vzťah daný rovnicami:
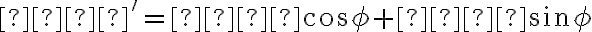
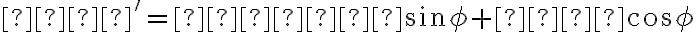
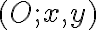 . Hovoríme, že nová sústava
. Hovoríme, že nová sústava 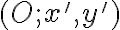 vznikla z pôvodnej sústavy
vznikla z pôvodnej sústavy 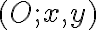
otočením okolo počiatku pôvodnej sústavy
 daným uhlom
daným uhlom 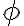 , ak platí medzi pôvodnými súradnicami
, ak platí medzi pôvodnými súradnicami 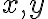
a novými súradnicami
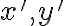 ľubovoľného bodu
ľubovoľného bodu  vzťah daný rovnicami:
vzťah daný rovnicami:
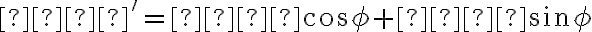
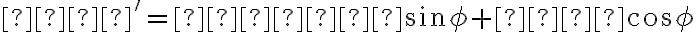
Všeobecná rovnica kužeľosečky obsahuje zmiešaný kvadratický člen 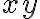 :
:
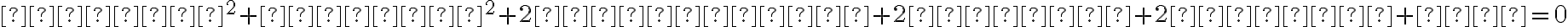 .
.
Ak chceme, aby vypadol zmiešaný kvadratický člen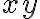 v príslušnej všeobecnej rovnici kužeľosečky,
v príslušnej všeobecnej rovnici kužeľosečky,
tak otočíme pôvodnú súradnicovú sústavu okolo počiatku o taký uhol
o taký uhol 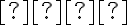 , aby koeficient
, aby koeficient 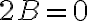 a všeobecná kužeľosečka mala tvar:
a všeobecná kužeľosečka mala tvar:
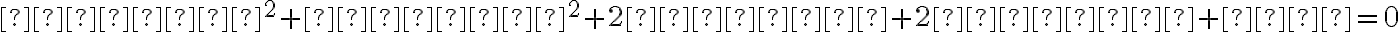 .
.
Najprv všeobecne transformujeme pôvodnú súradnicovú sústavu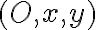 otočením na novú súradnicovú sústavu
otočením na novú súradnicovú sústavu 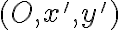 :
:
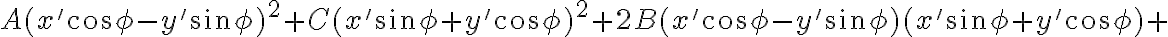
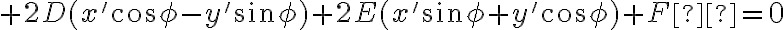 .
.
Pomocou algebrických úprav dostaneme nasledujúci tvar všeobecnej rovnice v otočení:
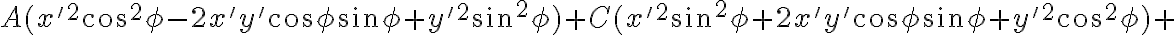
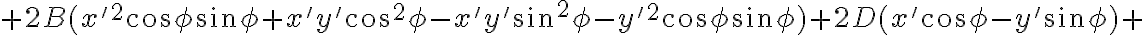
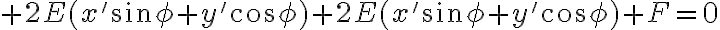
Vyjadríme si koeficient pri zmiešanom kvadratickom člene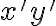 :
:
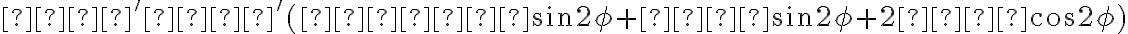 .
.
Keďže chceme odstrániť zmiešaný kvadratický člen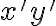 , tak potom musí platiť:
, tak potom musí platiť:
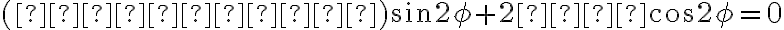 .
.
Vyjadríme si nakoniec, o aký uhol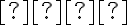 musíme otočiť príslušnú kužeľosečku,
musíme otočiť príslušnú kužeľosečku,
aby sme odstránili zmiešaný kvadratický člen zo všeobecnej rovnice danej kužeľosečky:
zo všeobecnej rovnice danej kužeľosečky:
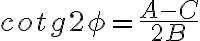
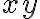 :
:
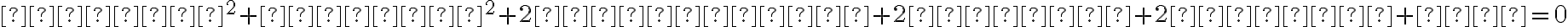 .
.
Ak chceme, aby vypadol zmiešaný kvadratický člen
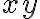 v príslušnej všeobecnej rovnici kužeľosečky,
v príslušnej všeobecnej rovnici kužeľosečky,
tak otočíme pôvodnú súradnicovú sústavu okolo počiatku
 o taký uhol
o taký uhol 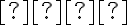 , aby koeficient
, aby koeficient 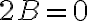 a všeobecná kužeľosečka mala tvar:
a všeobecná kužeľosečka mala tvar:
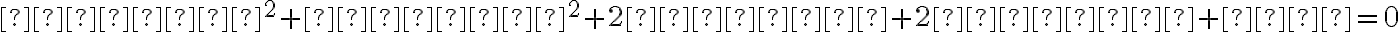 .
.
Najprv všeobecne transformujeme pôvodnú súradnicovú sústavu
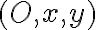 otočením na novú súradnicovú sústavu
otočením na novú súradnicovú sústavu 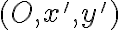 :
:
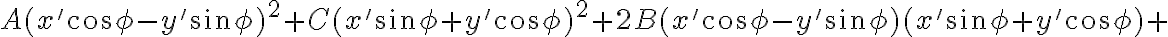
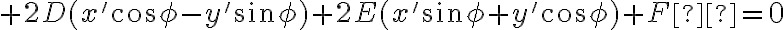 .
.
Pomocou algebrických úprav dostaneme nasledujúci tvar všeobecnej rovnice v otočení:
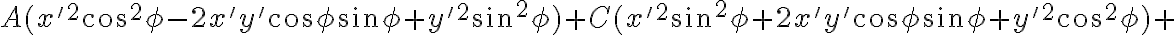
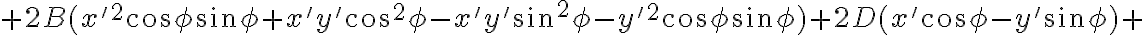
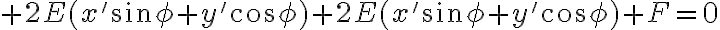
Vyjadríme si koeficient pri zmiešanom kvadratickom člene
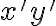 :
:
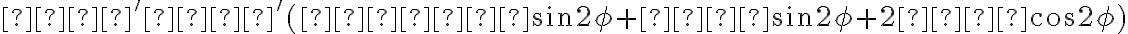 .
.
Keďže chceme odstrániť zmiešaný kvadratický člen
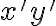 , tak potom musí platiť:
, tak potom musí platiť:
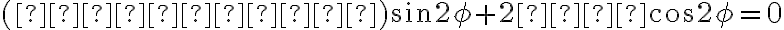 .
.
Vyjadríme si nakoniec, o aký uhol
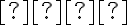 musíme otočiť príslušnú kužeľosečku,
musíme otočiť príslušnú kužeľosečku,
aby sme odstránili zmiešaný kvadratický člen
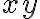 zo všeobecnej rovnice danej kužeľosečky:
zo všeobecnej rovnice danej kužeľosečky:
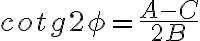
6.3. Výpočtové úlohy
Príklad 1: Určte prienik kružnice  a priamky
a priamky  v závislosti od parametra
v závislosti od parametra  :
:
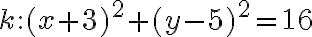
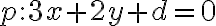
Riešenie príkladu v GeoGebre.

 a priamky
a priamky  v závislosti od parametra
v závislosti od parametra  :
:
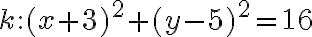
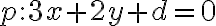
Riešenie príkladu v GeoGebre.

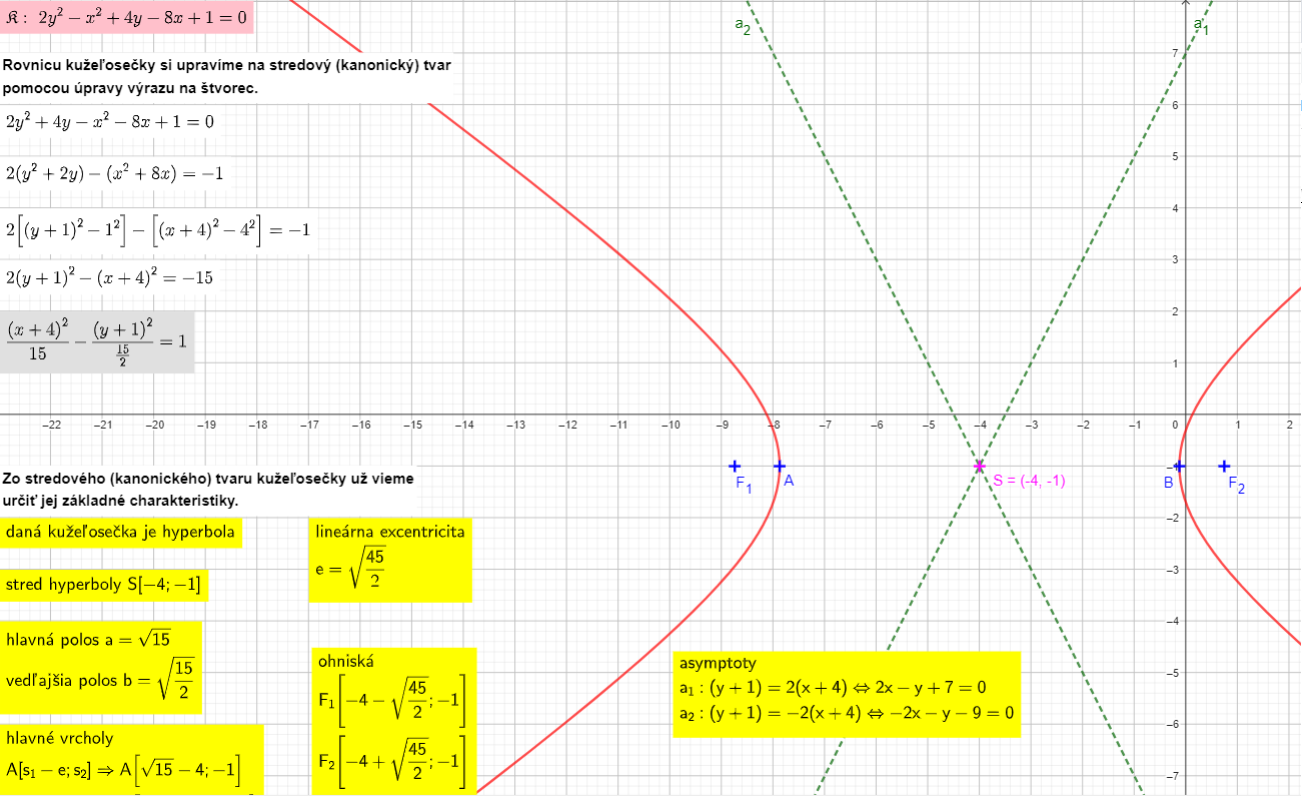
Príklad 2: Daná je kužeľosečka rovnicou 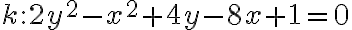 . Určte jej základné charakteristické prvky a načrtnite ju.
. Určte jej základné charakteristické prvky a načrtnite ju.
Riešenie príkladu v GeoGebre.
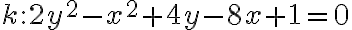 . Určte jej základné charakteristické prvky a načrtnite ju.
. Určte jej základné charakteristické prvky a načrtnite ju.
Riešenie príkladu v GeoGebre.

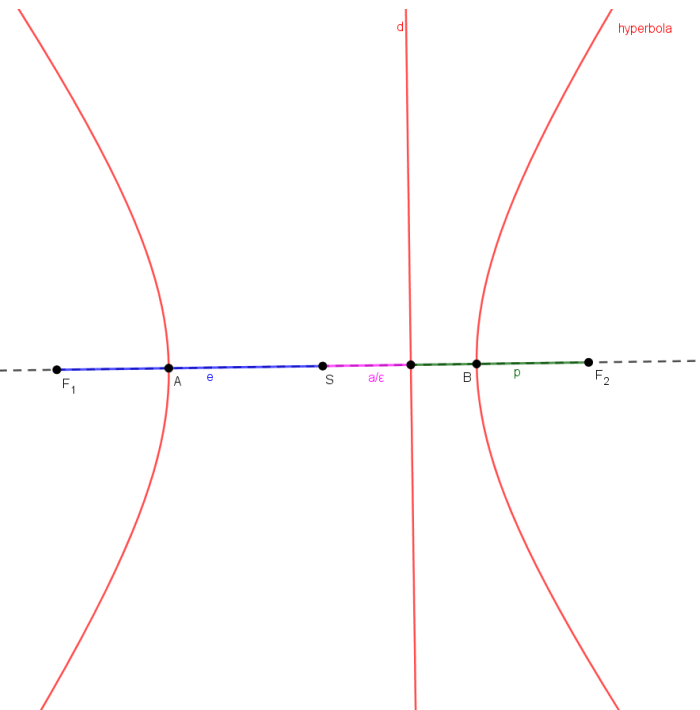
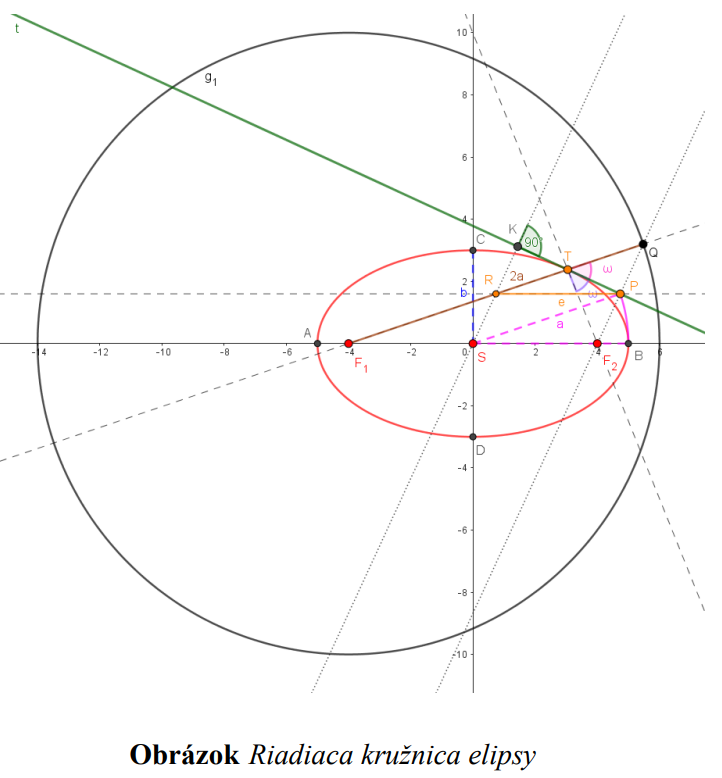
7. Riadiaca priamka kužeľosečky
Riadiacimi priamkami 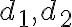 elipsy (hyperboly) nazývame také priamky, ktoré sú kolmé na hlavnú os
elipsy (hyperboly) nazývame také priamky, ktoré sú kolmé na hlavnú os  vo vzdialenosti
vo vzdialenosti 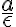
od stredu kužeľosečky , kde
, kde  je numerická výstrednosť (excentricita) elipsy, resp. hyperboly.
je numerická výstrednosť (excentricita) elipsy, resp. hyperboly.
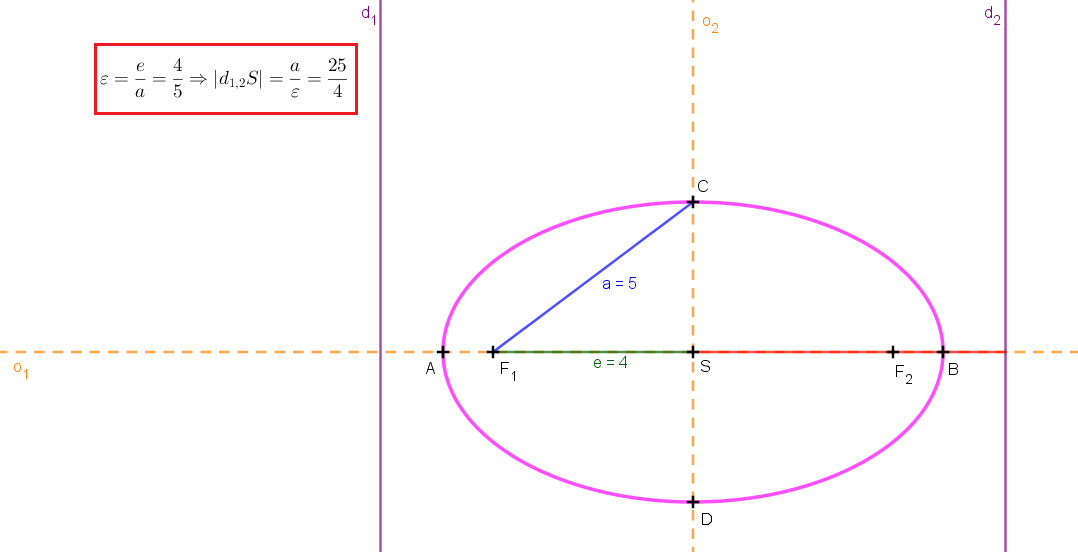
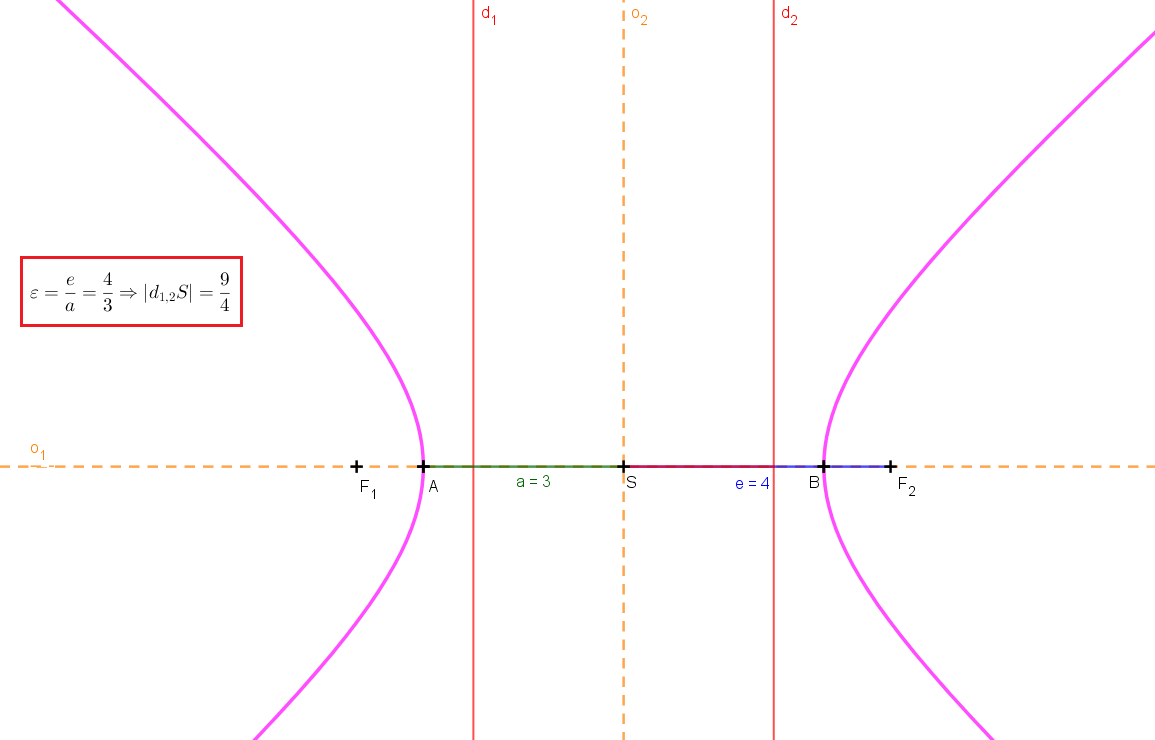
Obrázok Riadiace priamky hyperboly
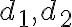 elipsy (hyperboly) nazývame také priamky, ktoré sú kolmé na hlavnú os
elipsy (hyperboly) nazývame také priamky, ktoré sú kolmé na hlavnú os  vo vzdialenosti
vo vzdialenosti 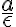
od stredu kužeľosečky
 , kde
, kde  je numerická výstrednosť (excentricita) elipsy, resp. hyperboly.
je numerická výstrednosť (excentricita) elipsy, resp. hyperboly.

Obrázok Riadiace priamky elipsy

Obrázok Riadiace priamky hyperboly
Regulárne kužeľosečky a ich riadiace priamky:
Regulárna kužeľosečka je množina bodov roviny, ktoré majú od pevne zvoleného bodu
a riadiacej priamky stály pomer vzdialeností rovný numerickej excentricite
stály pomer vzdialeností rovný numerickej excentricite  :
:
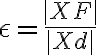 ,
,
kde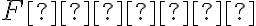 , pričom ďalej platí, že ak:
, pričom ďalej platí, že ak:
•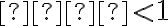 , potom kužeľosečka je elipsa
, potom kužeľosečka je elipsa
•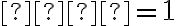 , potom kužeľosečka je parabola
, potom kužeľosečka je parabola
•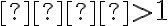 , potom kužeľosečka je hyperbola.
, potom kužeľosečka je hyperbola.
Regulárna kužeľosečka je množina bodov roviny, ktoré majú od pevne zvoleného bodu

a riadiacej priamky
 stály pomer vzdialeností rovný numerickej excentricite
stály pomer vzdialeností rovný numerickej excentricite 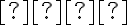 :
:
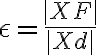 ,
,
kde
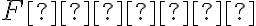 , pričom ďalej platí, že ak:
, pričom ďalej platí, že ak:
•
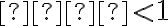 , potom kužeľosečka je elipsa
, potom kužeľosečka je elipsa
•
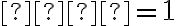 , potom kužeľosečka je parabola
, potom kužeľosečka je parabola
•
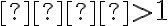 , potom kužeľosečka je hyperbola.
, potom kužeľosečka je hyperbola.
Singulárne kužeľosečky a ich riadiace priamky:
Singulárna kužeľosečka je množina bodov roviny, ktoré majú od pevne zvoleného bodu
a riadiacej priamky stály pomer vzdialeností rovný numerickej excentricite
stály pomer vzdialeností rovný numerickej excentricite 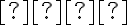 :
:
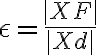 ,
,
kde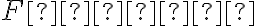 , pričom ďalej platí, že ak:
, pričom ďalej platí, že ak:
•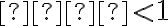 , potom kužeľosečka je prázdna množina
, potom kužeľosečka je prázdna množina
•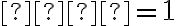 , potom kužeľosečka je totožné rovnobežky okrem bodu
, potom kužeľosečka je totožné rovnobežky okrem bodu 
•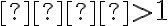 , potom kužeľosečka je zjednotenie rôznobežiek okrem bodu
, potom kužeľosečka je zjednotenie rôznobežiek okrem bodu  .
.
Singulárna kužeľosečka je množina bodov roviny, ktoré majú od pevne zvoleného bodu

a riadiacej priamky
 stály pomer vzdialeností rovný numerickej excentricite
stály pomer vzdialeností rovný numerickej excentricite 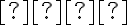 :
:
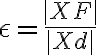 ,
,
kde
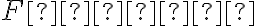 , pričom ďalej platí, že ak:
, pričom ďalej platí, že ak:
•
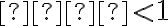 , potom kužeľosečka je prázdna množina
, potom kužeľosečka je prázdna množina
•
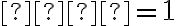 , potom kužeľosečka je totožné rovnobežky okrem bodu
, potom kužeľosečka je totožné rovnobežky okrem bodu 
•
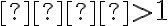 , potom kužeľosečka je zjednotenie rôznobežiek okrem bodu
, potom kužeľosečka je zjednotenie rôznobežiek okrem bodu  .
.
7.1. Dôkaz vety pre regulárne kužeľosečky
Nech súradnicová os 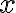 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza bodom
a prechádza bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X[x; y] X[x; y]](https://lms.umb.sk/filter/tex/pix.php/4ac2c3ad15e55af00f37154fc98bdc57.png) platí,
platí,
že neležia na riadiacej priamke , preto
, preto 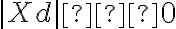 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
:
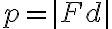 .
.
Pre označenie ďalších potrebných vzdialeností si pomôžeme nasledujúcim obrázkom
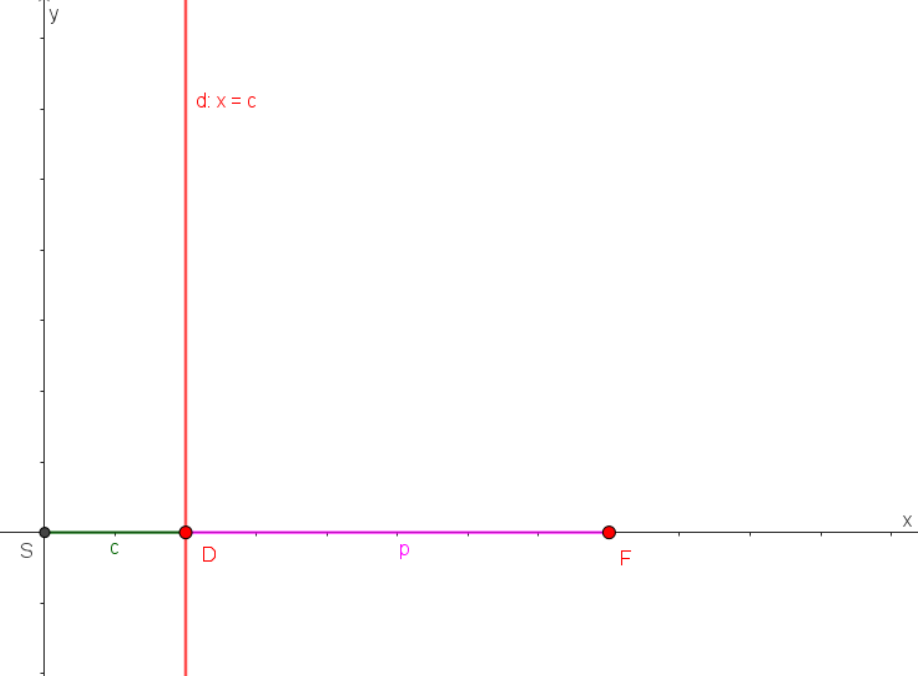
Vidíme na obrázku, že súradnice pevne zvoleného bodu sú![F[e; 0] F[e; 0]](https://lms.umb.sk/filter/tex/pix.php/053dae281ef4069bc7dab12eafb2a293.png) , kde
, kde 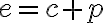 , riadiaca priamka
, riadiaca priamka  je
popísaná rovnicou
je
popísaná rovnicou 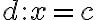 .
.
Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi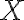 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  , platí:
, platí:
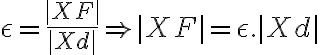
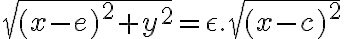
Vytvoríme kvadratickú rovnicu s neznámymi x, y, keďže kužeľosečky sú krivky 2. stupňa:
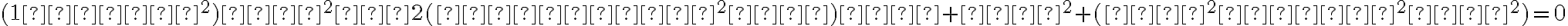 .
.
Nech počiatok KSS je zvolený tak, aby v kvadratickej rovnici vypadol absolútny člen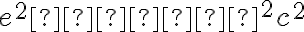 , takže potom
, takže potom 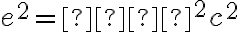 .
.
Keďže možnosť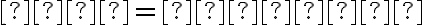 nevyhovuje pre ľubovoľné kladné
nevyhovuje pre ľubovoľné kladné 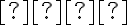 , tak budeme predpokladať, že
, tak budeme predpokladať, že 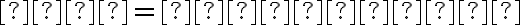 .
.
Odvodená kvadratická rovnica nadobudne tzv. vrcholový tvar všeobecnej rovnice kužeľosečky:
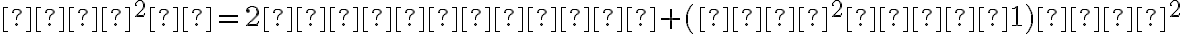 .
.
Z definície riadiacej priamky kužeľosečky vyplýva, že vzdialenosť stredu príslušnej kužeľosečky od riadiacej priamky
od riadiacej priamky  je rovná:
je rovná:
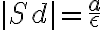
Ďalej sme si označili vzdialenosť pevne zvoleného bodu od riadiacej priamky
od riadiacej priamky 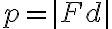 .
.
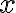 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza bodom
a prechádza bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X[x; y] X[x; y]](https://lms.umb.sk/filter/tex/pix.php/4ac2c3ad15e55af00f37154fc98bdc57.png) platí,
platí,
že neležia na riadiacej priamke
 , preto
, preto 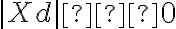 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
:
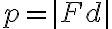 .
.
Pre označenie ďalších potrebných vzdialeností si pomôžeme nasledujúcim obrázkom

Vidíme na obrázku, že súradnice pevne zvoleného bodu sú
![F[e; 0] F[e; 0]](https://lms.umb.sk/filter/tex/pix.php/053dae281ef4069bc7dab12eafb2a293.png) , kde
, kde 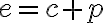 , riadiaca priamka
, riadiaca priamka  je
popísaná rovnicou
je
popísaná rovnicou 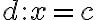 .
.
Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi
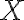 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  , platí:
, platí:
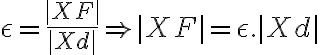
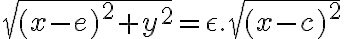
Vytvoríme kvadratickú rovnicu s neznámymi x, y, keďže kužeľosečky sú krivky 2. stupňa:
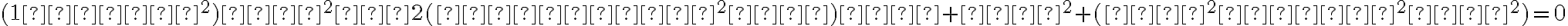 .
.
Nech počiatok KSS je zvolený tak, aby v kvadratickej rovnici vypadol absolútny člen
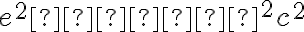 , takže potom
, takže potom 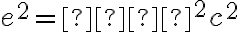 .
.
Keďže možnosť
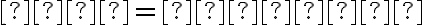 nevyhovuje pre ľubovoľné kladné
nevyhovuje pre ľubovoľné kladné 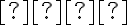 , tak budeme predpokladať, že
, tak budeme predpokladať, že 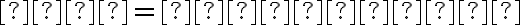 .
.
Odvodená kvadratická rovnica nadobudne tzv. vrcholový tvar všeobecnej rovnice kužeľosečky:
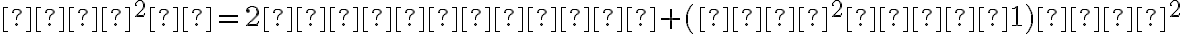 .
.
Z definície riadiacej priamky kužeľosečky vyplýva, že vzdialenosť stredu príslušnej kužeľosečky
 od riadiacej priamky
od riadiacej priamky  je rovná:
je rovná:
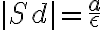
Ďalej sme si označili vzdialenosť pevne zvoleného bodu
 od riadiacej priamky
od riadiacej priamky 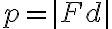 .
.
Najprv ukážeme platnosť vety pre elipsu. Pomôžeme si nasledujúcim obrázkom:
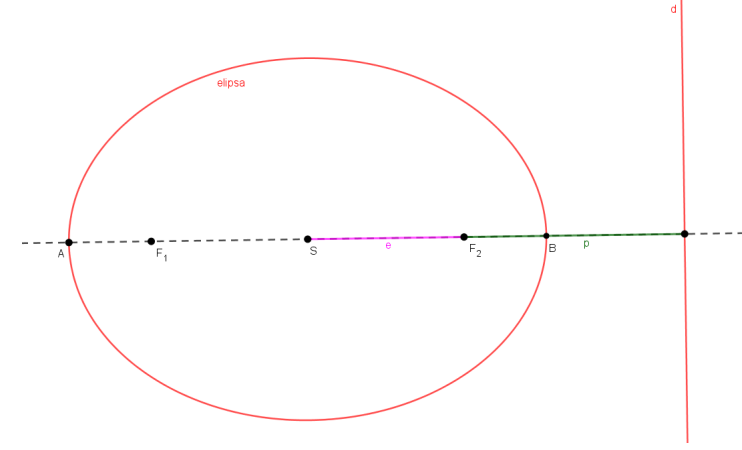
Pomocou obrázka si vyjadríme parameter p:
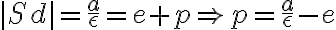
Vyjadrený parameter p dosadíme do vrcholovej rovnice kužeľosečky:
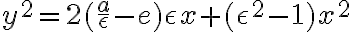
Túto rovnicu postupne upravíme na stredový tvar elipsy, pričom dosadíme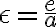 :
:
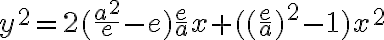
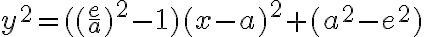
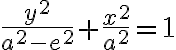
Dostali sme stredovú rovnicu elipsy.

Pomocou obrázka si vyjadríme parameter p:
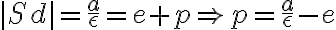
Vyjadrený parameter p dosadíme do vrcholovej rovnice kužeľosečky:
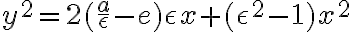
Túto rovnicu postupne upravíme na stredový tvar elipsy, pričom dosadíme
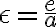 :
:
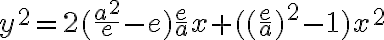
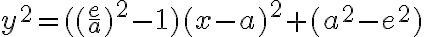
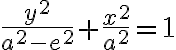
Dostali sme stredovú rovnicu elipsy.
Pre parabolu predpokladáme, že 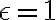 . Potom vrcholová rovnica kužeľosečky má tvar:
. Potom vrcholová rovnica kužeľosečky má tvar:
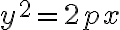
Zrejme ide o vrcholovú rovnicu paraboly.
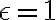 . Potom vrcholová rovnica kužeľosečky má tvar:
. Potom vrcholová rovnica kužeľosečky má tvar: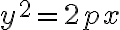
Zrejme ide o vrcholovú rovnicu paraboly.
7.2. Dôkaz vety pre singulárne kužeľosečky
Nech súradnicová os 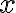 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza pevným bodom
a prechádza pevným bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X [x; y] X [x; y]](https://lms.umb.sk/filter/tex/pix.php/77046f7175b62e08861002c3fc77c3a3.png) platí, že neležia na riadiacej priamke
platí, že neležia na riadiacej priamke  , preto
, preto 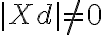 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
:
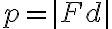 .
.
Súradnice pevne zvoleného bodu sú![F[e;0] F[e;0]](https://lms.umb.sk/filter/tex/pix.php/d45ce59d231cd820e6eddd0c9b0e2176.png) , pričom
, pričom 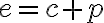 a koeficient
a koeficient 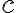 je z rovnice popisujúcu riadiacu priamku
je z rovnice popisujúcu riadiacu priamku 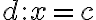 . Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny
. Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny 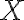 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  platí:
platí:
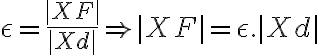
Podrobnejšie si rozoberieme dané vzdialenosti:
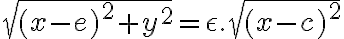
Vytvoríme kvadratickú rovnicu s neznámymi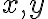 , keďže kužeľosečky sú algebrické krivky 2. stupňa:
, keďže kužeľosečky sú algebrické krivky 2. stupňa:
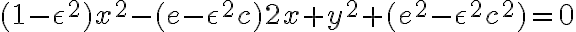
Keďže pevný bod leží na riadiacej priamke
leží na riadiacej priamke  , tak platí
, tak platí 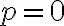 . Riadiaca priamka
. Riadiaca priamka  je vzdialená od počiatku KSS o konštantu
je vzdialená od počiatku KSS o konštantu 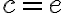 . Vytvorená kvadratická rovnica s neznámymi
. Vytvorená kvadratická rovnica s neznámymi 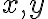 nadobudne nasledujúci tvar:
nadobudne nasledujúci tvar:
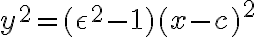
Pomocou poslednej odvodenej rovnice sa budeme zaoberať prípadmi s veľkosťami numerickej excentricity:
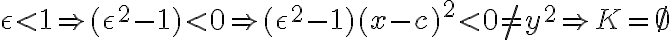 - dostali sme prázdnu množinu
- dostali sme prázdnu množinu
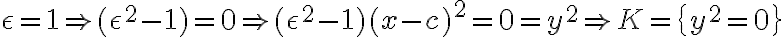 - dostali sme totožné rovnobežky
- dostali sme totožné rovnobežky
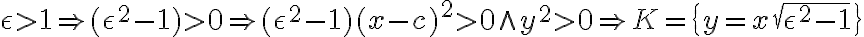 - dostali sme zjednotenie rôznobežiek.
- dostali sme zjednotenie rôznobežiek.
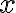 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza pevným bodom
a prechádza pevným bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X [x; y] X [x; y]](https://lms.umb.sk/filter/tex/pix.php/77046f7175b62e08861002c3fc77c3a3.png) platí, že neležia na riadiacej priamke
platí, že neležia na riadiacej priamke  , preto
, preto 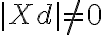 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
: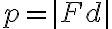 .
.Súradnice pevne zvoleného bodu sú
![F[e;0] F[e;0]](https://lms.umb.sk/filter/tex/pix.php/d45ce59d231cd820e6eddd0c9b0e2176.png) , pričom
, pričom 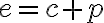 a koeficient
a koeficient 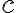 je z rovnice popisujúcu riadiacu priamku
je z rovnice popisujúcu riadiacu priamku 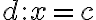 . Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny
. Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi roviny 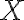 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  platí:
platí: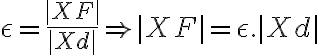
Podrobnejšie si rozoberieme dané vzdialenosti:
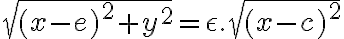
Vytvoríme kvadratickú rovnicu s neznámymi
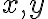 , keďže kužeľosečky sú algebrické krivky 2. stupňa:
, keďže kužeľosečky sú algebrické krivky 2. stupňa: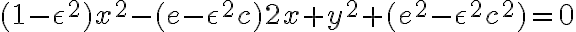
Keďže pevný bod
 leží na riadiacej priamke
leží na riadiacej priamke  , tak platí
, tak platí 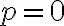 . Riadiaca priamka
. Riadiaca priamka  je vzdialená od počiatku KSS o konštantu
je vzdialená od počiatku KSS o konštantu 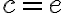 . Vytvorená kvadratická rovnica s neznámymi
. Vytvorená kvadratická rovnica s neznámymi 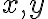 nadobudne nasledujúci tvar:
nadobudne nasledujúci tvar: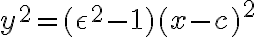
Pomocou poslednej odvodenej rovnice sa budeme zaoberať prípadmi s veľkosťami numerickej excentricity:
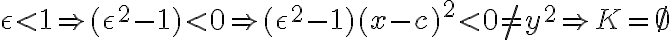 - dostali sme prázdnu množinu
- dostali sme prázdnu množinu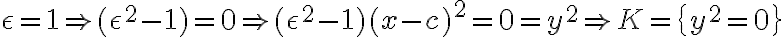 - dostali sme totožné rovnobežky
- dostali sme totožné rovnobežky 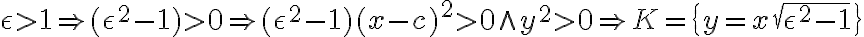 - dostali sme zjednotenie rôznobežiek.
- dostali sme zjednotenie rôznobežiek.