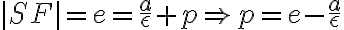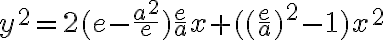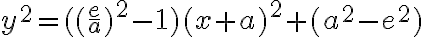Kubovčík, M.: Kužeľosečky
7. Riadiaca priamka kužeľosečky
7.1. Dôkaz vety pre regulárne kužeľosečky
Nech súradnicová os 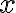 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza bodom
a prechádza bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X[x; y] X[x; y]](https://lms.umb.sk/filter/tex/pix.php/4ac2c3ad15e55af00f37154fc98bdc57.png) platí,
platí,
že neležia na riadiacej priamke , preto
, preto 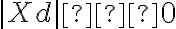 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
:
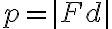 .
.
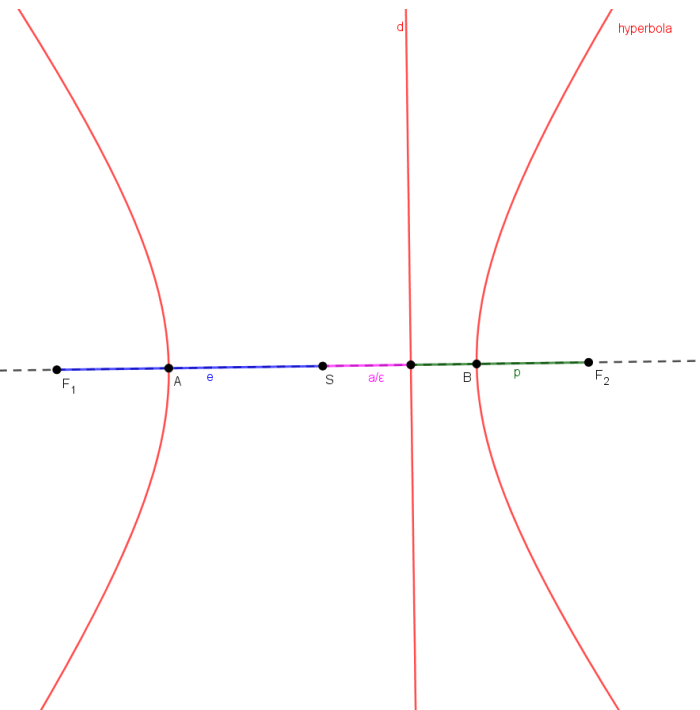
Pre označenie ďalších potrebných vzdialeností si pomôžeme nasledujúcim obrázkom
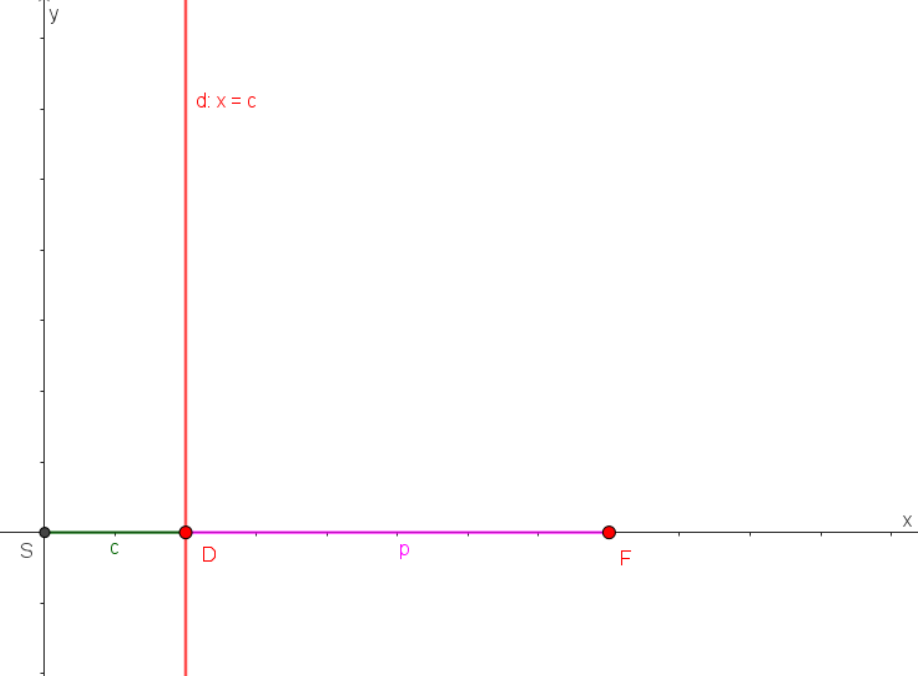
Vidíme na obrázku, že súradnice pevne zvoleného bodu sú![F[e; 0] F[e; 0]](https://lms.umb.sk/filter/tex/pix.php/053dae281ef4069bc7dab12eafb2a293.png) , kde
, kde 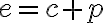 , riadiaca priamka
, riadiaca priamka  je
popísaná rovnicou
je
popísaná rovnicou 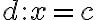 .
.
Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi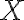 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  , platí:
, platí:
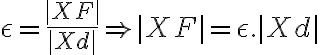
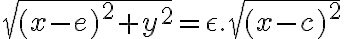
Vytvoríme kvadratickú rovnicu s neznámymi x, y, keďže kužeľosečky sú krivky 2. stupňa:
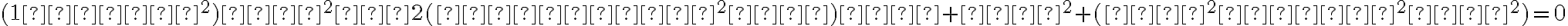 .
.
Nech počiatok KSS je zvolený tak, aby v kvadratickej rovnici vypadol absolútny člen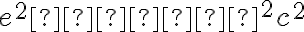 , takže potom
, takže potom 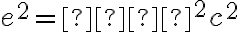 .
.
Keďže možnosť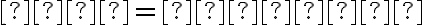 nevyhovuje pre ľubovoľné kladné
nevyhovuje pre ľubovoľné kladné 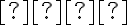 , tak budeme predpokladať, že
, tak budeme predpokladať, že 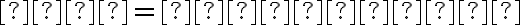 .
.
Odvodená kvadratická rovnica nadobudne tzv. vrcholový tvar všeobecnej rovnice kužeľosečky:
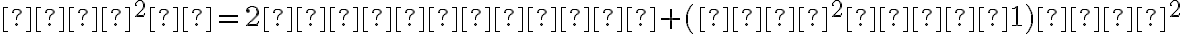 .
.
Z definície riadiacej priamky kužeľosečky vyplýva, že vzdialenosť stredu príslušnej kužeľosečky od riadiacej priamky
od riadiacej priamky  je rovná:
je rovná:
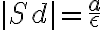
Ďalej sme si označili vzdialenosť pevne zvoleného bodu od riadiacej priamky
od riadiacej priamky 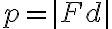 .
.
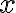 KSS je kolmá na riadiacu priamku
KSS je kolmá na riadiacu priamku  a prechádza bodom
a prechádza bodom  . Pre hľadané body roviny
. Pre hľadané body roviny ![X[x; y] X[x; y]](https://lms.umb.sk/filter/tex/pix.php/4ac2c3ad15e55af00f37154fc98bdc57.png) platí,
platí,
že neležia na riadiacej priamke
 , preto
, preto 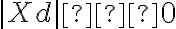 . Označme
. Označme  vzdialenosť daného bodu
vzdialenosť daného bodu  od danej riadiacej priamky
od danej riadiacej priamky  :
:
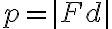 .
.
Pre označenie ďalších potrebných vzdialeností si pomôžeme nasledujúcim obrázkom

Vidíme na obrázku, že súradnice pevne zvoleného bodu sú
![F[e; 0] F[e; 0]](https://lms.umb.sk/filter/tex/pix.php/053dae281ef4069bc7dab12eafb2a293.png) , kde
, kde 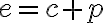 , riadiaca priamka
, riadiaca priamka  je
popísaná rovnicou
je
popísaná rovnicou 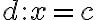 .
.
Pre numerickú výstrednosť danej kužeľosečky, ktorá je popísaná bodmi
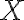 , pevne zvoleným bodom
, pevne zvoleným bodom  a riadiacou priamkou
a riadiacou priamkou  , platí:
, platí:
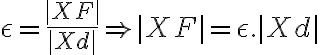
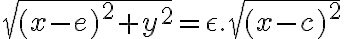
Vytvoríme kvadratickú rovnicu s neznámymi x, y, keďže kužeľosečky sú krivky 2. stupňa:
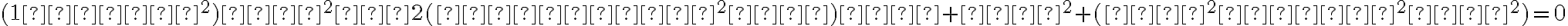 .
.
Nech počiatok KSS je zvolený tak, aby v kvadratickej rovnici vypadol absolútny člen
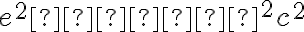 , takže potom
, takže potom 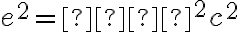 .
.
Keďže možnosť
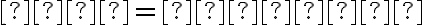 nevyhovuje pre ľubovoľné kladné
nevyhovuje pre ľubovoľné kladné 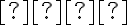 , tak budeme predpokladať, že
, tak budeme predpokladať, že 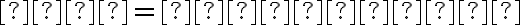 .
.
Odvodená kvadratická rovnica nadobudne tzv. vrcholový tvar všeobecnej rovnice kužeľosečky:
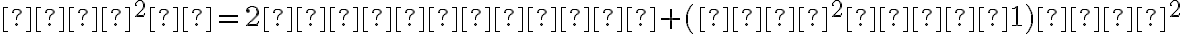 .
.
Z definície riadiacej priamky kužeľosečky vyplýva, že vzdialenosť stredu príslušnej kužeľosečky
 od riadiacej priamky
od riadiacej priamky  je rovná:
je rovná:
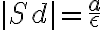
Ďalej sme si označili vzdialenosť pevne zvoleného bodu
 od riadiacej priamky
od riadiacej priamky 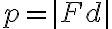 .
.
Najprv ukážeme platnosť vety pre elipsu. Pomôžeme si nasledujúcim obrázkom:
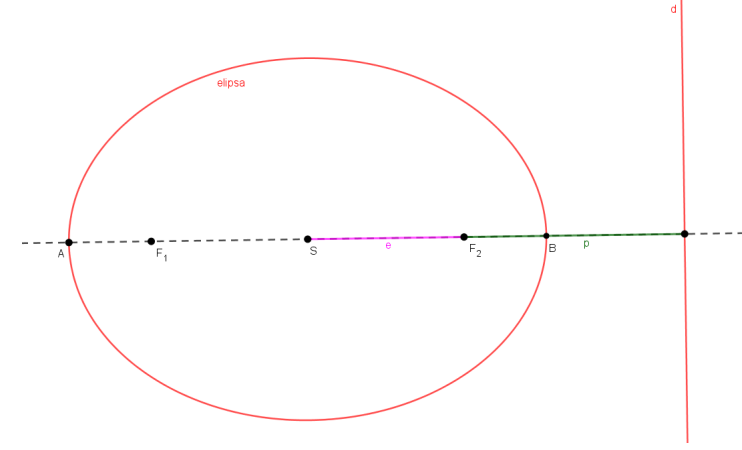
Pomocou obrázka si vyjadríme parameter p:
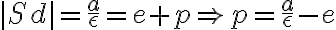
Vyjadrený parameter p dosadíme do vrcholovej rovnice kužeľosečky:
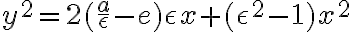
Túto rovnicu postupne upravíme na stredový tvar elipsy, pričom dosadíme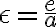 :
:
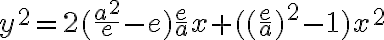
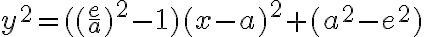
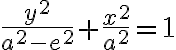
Dostali sme stredovú rovnicu elipsy.

Pomocou obrázka si vyjadríme parameter p:
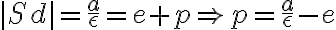
Vyjadrený parameter p dosadíme do vrcholovej rovnice kužeľosečky:
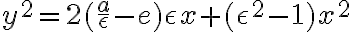
Túto rovnicu postupne upravíme na stredový tvar elipsy, pričom dosadíme
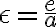 :
:
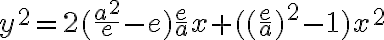
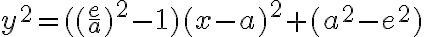
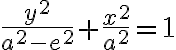
Dostali sme stredovú rovnicu elipsy.
Pre parabolu predpokladáme, že 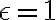 . Potom vrcholová rovnica kužeľosečky má tvar:
. Potom vrcholová rovnica kužeľosečky má tvar:
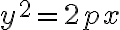
Zrejme ide o vrcholovú rovnicu paraboly.
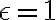 . Potom vrcholová rovnica kužeľosečky má tvar:
. Potom vrcholová rovnica kužeľosečky má tvar: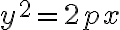
Zrejme ide o vrcholovú rovnicu paraboly.