Kubovčík, M.: Kužeľosečky
6. Analytické vyjadrenie kužeľosečiek
6.1. Stredová a vrcholová rovnica kužeľosečky
Elipsa 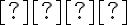 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých súčet vzdialeností od dvoch pevných bodov (ohnísk) je stály a rovný
je stály a rovný 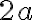 , pričom konštanta
, pričom konštanta 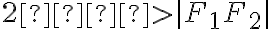 :
:
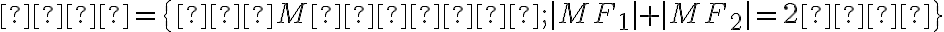 .
.
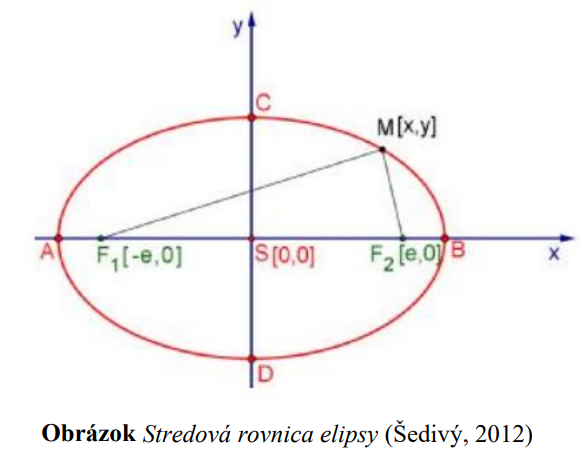
Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom elipsy, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme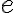 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod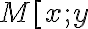 ] na elipse
] na elipse  práve vtedy, keď platí:
práve vtedy, keď platí:
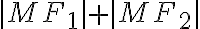 =
=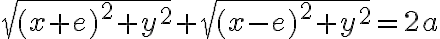 .
.
Ďalším umocňovaním a úpravami dostaneme:
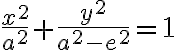 .
.
Ak stred elipsy je bod![S[m; n] S[m; n]](https://lms.umb.sk/filter/tex/pix.php/5052e1eedc1daed03437c681e8aa3d8e.png) a ohniská ležia na rovnobežke s osou
a ohniská ležia na rovnobežke s osou 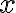 prechádzajúcou bodom
prechádzajúcou bodom  , potom stredová rovnica elipsy:
, potom stredová rovnica elipsy:
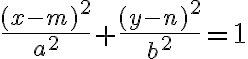 .
.
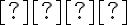 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých súčet vzdialeností od dvoch pevných bodov (ohnísk)
 je stály a rovný
je stály a rovný 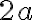 , pričom konštanta
, pričom konštanta 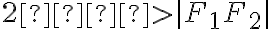 :
:
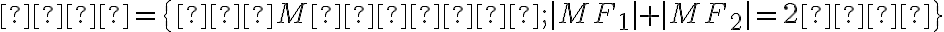 .
.

Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom elipsy, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme
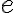 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod
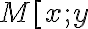 ] na elipse
] na elipse  práve vtedy, keď platí:
práve vtedy, keď platí:
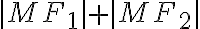 =
=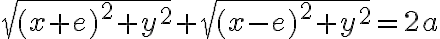 .
.
Ďalším umocňovaním a úpravami dostaneme:
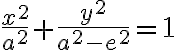 .
.
Ak stred elipsy je bod
![S[m; n] S[m; n]](https://lms.umb.sk/filter/tex/pix.php/5052e1eedc1daed03437c681e8aa3d8e.png) a ohniská ležia na rovnobežke s osou
a ohniská ležia na rovnobežke s osou  prechádzajúcou bodom
prechádzajúcou bodom  , potom stredová rovnica elipsy:
, potom stredová rovnica elipsy:
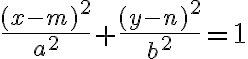 .
.
Hyperbola  je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých rozdiel vzdialeností od dvoch pevných bodov (ohnísk) je stály a rovný
je stály a rovný 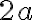 , pričom konštanta
, pričom konštanta 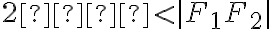 :
:
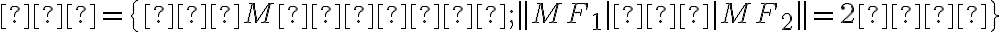 .
.
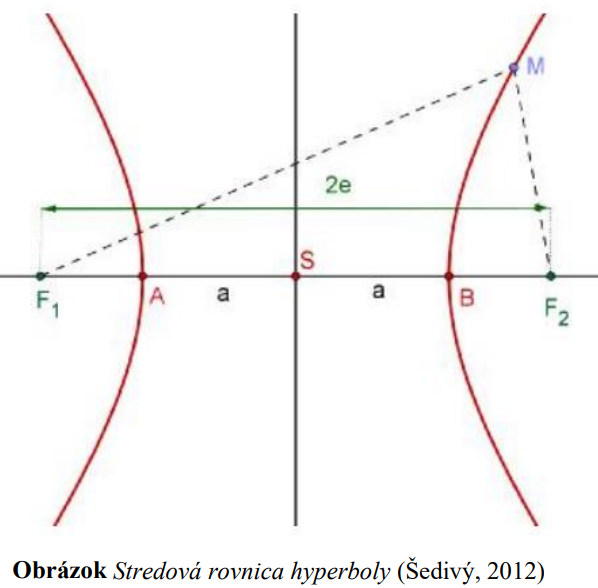
Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom hyperboly, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme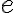 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/05b89453b51c3ac375aeacbc6a7f181d.png) na hyperbole
na hyperbole 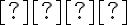 práve vtedy, keď platí:
práve vtedy, keď platí:
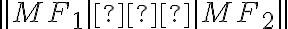 =|
=|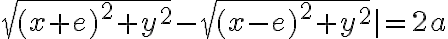 .
.
Ďalším umocňovaním a úpravami dostaneme:
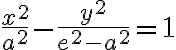 .
.
Ak stred hyperboly je bod S[m; n] a ohniská ležia na rovnobežke s osou x prechádzajúcou bodom S, potom stredová rovnica hyperboly:
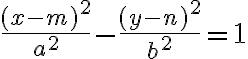 .
.
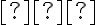 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktorých rozdiel vzdialeností od dvoch pevných bodov (ohnísk)
 je stály a rovný
je stály a rovný 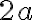 , pričom konštanta
, pričom konštanta 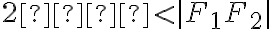 :
:
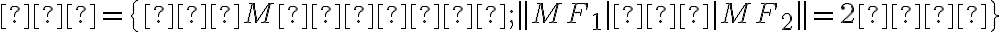 .
.

Počiatok karteziánskej sústave súradníc (KSS) stotožníme so stredom hyperboly, hlavná a vedľajšia os elipsy je totožná s osami KSS
a vzdialenosť ohnísk od stredu označíme
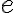 (lineárna excentricita). Potom pre súradnice týchto bodov platí:
(lineárna excentricita). Potom pre súradnice týchto bodov platí:
![S[0; 0], F_1[-e; 0], F_2[e; 0] S[0; 0], F_1[-e; 0], F_2[e; 0]](https://lms.umb.sk/filter/tex/pix.php/3fbd2bcfb1655c7db06945c1db05722e.png) .
.
Podľa definície leží bod
![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/05b89453b51c3ac375aeacbc6a7f181d.png) na hyperbole
na hyperbole 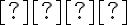 práve vtedy, keď platí:
práve vtedy, keď platí:
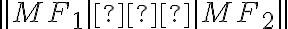 =|
=|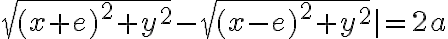 .
.
Ďalším umocňovaním a úpravami dostaneme:
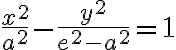 .
.
Ak stred hyperboly je bod S[m; n] a ohniská ležia na rovnobežke s osou x prechádzajúcou bodom S, potom stredová rovnica hyperboly:
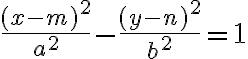 .
.
Parabola 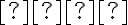 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktoré majú rovnakú vzdialenosť od pevného bodu (ohnisko) a pevnej (riadiacej) priamky
a pevnej (riadiacej) priamky  :
:
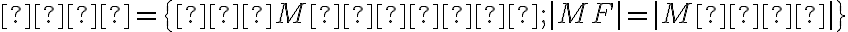 .
.
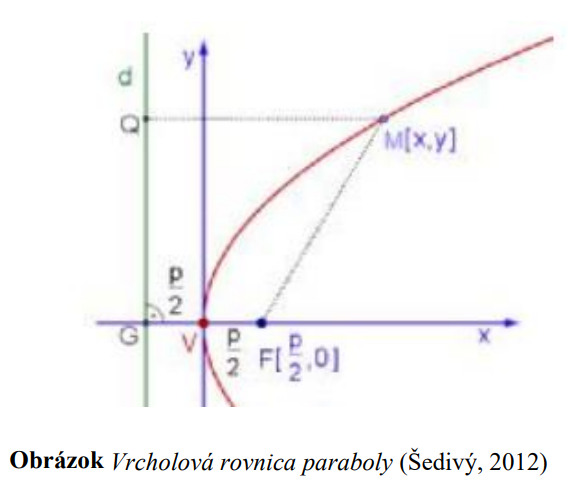
Parabolu v KSS umiestnime tak, aby vrchol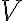 ležal na jej počiatku. Riadiacu priamku paraboly
ležal na jej počiatku. Riadiacu priamku paraboly  vieme popísať rovnicou
vieme popísať rovnicou
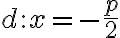 .
.
Ohnisko má súradnice![F[𝑝/2; 0] F[𝑝/2; 0]](https://lms.umb.sk/filter/tex/pix.php/a71f3cee78cfc5827342208f2a3b5e07.png) . Podľa definície leží bod
. Podľa definície leží bod ![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/cf2a1516111d0aba727db8b6611dc143.png) na parabole
na parabole 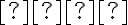 práve vtedy, keď platí:
práve vtedy, keď platí:
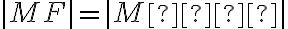 .
.
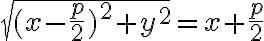 .
.
Ďalším umocňovaním a úpravami dostaneme:
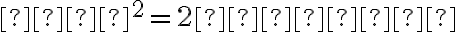 .
.
Ak vrchol paraboly je bod![V[m; n] V[m; n]](https://lms.umb.sk/filter/tex/pix.php/5088170b081e7fea2f4e42bface36dc0.png) a ohnisko leží na rovnobežke s osou
a ohnisko leží na rovnobežke s osou 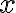 prechádzajúcou bodom
prechádzajúcou bodom 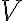 , potom vrcholová rovnica paraboly:
, potom vrcholová rovnica paraboly:
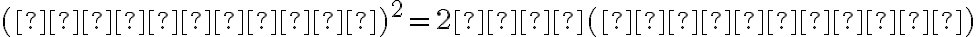 .
.
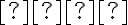 je množina všetkých bodov
je množina všetkých bodov  roviny
roviny  ,
,
ktoré majú rovnakú vzdialenosť od pevného bodu (ohnisko)
 a pevnej (riadiacej) priamky
a pevnej (riadiacej) priamky  :
:
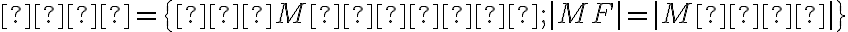 .
.

Parabolu v KSS umiestnime tak, aby vrchol
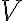 ležal na jej počiatku. Riadiacu priamku paraboly
ležal na jej počiatku. Riadiacu priamku paraboly  vieme popísať rovnicou
vieme popísať rovnicou
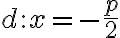 .
.
Ohnisko má súradnice
![F[𝑝/2; 0] F[𝑝/2; 0]](https://lms.umb.sk/filter/tex/pix.php/a71f3cee78cfc5827342208f2a3b5e07.png) . Podľa definície leží bod
. Podľa definície leží bod ![M[x; y] M[x; y]](https://lms.umb.sk/filter/tex/pix.php/cf2a1516111d0aba727db8b6611dc143.png) na parabole
na parabole 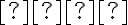 práve vtedy, keď platí:
práve vtedy, keď platí:
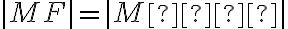 .
.
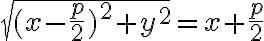 .
.
Ďalším umocňovaním a úpravami dostaneme:
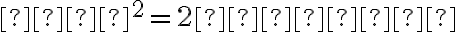 .
.
Ak vrchol paraboly je bod
![V[m; n] V[m; n]](https://lms.umb.sk/filter/tex/pix.php/5088170b081e7fea2f4e42bface36dc0.png) a ohnisko leží na rovnobežke s osou
a ohnisko leží na rovnobežke s osou 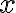 prechádzajúcou bodom
prechádzajúcou bodom 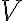 , potom vrcholová rovnica paraboly:
, potom vrcholová rovnica paraboly:
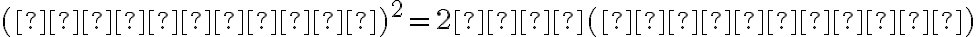 .
.
